برآورد درستنمایی بیشینه
در علم آمار برآورد حداکثر درستنمایی که بهطور خلاصه به آن MLE (مخفف عبارت انگلیسی maximum likelihood estimation) نیز گفته میشود) روشی است برای برآورد کردن پارامترهای یک مدل آماری. وقتی بر مجموعهای از دادهها عملیات انجام میشود یک مدل آماری به دست میآید آنگاه حداکثر درستنمایی میتواند تخمینی از پارامترهای مدل ارائه دهد. روش حداکثر درستنمایی به بسیاری از روشهای شناخته شدهٔ تخمین آماری شباهت دارد. فرض کنید برای شخصی اطلاعات مربوط به قد زرافههای ماده بالغ موجود در یک جمعیت مهم باشد و این شخص به خاطر محدودیت هزینه یا زمان نتواند قد تک تک این زرافهها را اندازه بگیرد، این شخص تنها میداند که این طول قدها از توزیع نرمال پیروی میکنند ولی میانگین و واریانس توزیع را نمیداند حال با استفاده از روش درستنمایی بیشینه و با در دست داشتن اطلاعات مربوط به نمونهای محدود از جمعیت میتواند تخمینی از میانگین و واریانس این توزیع بدست آورد.[1] MLE این کار را به این ترتیب انجام میدهد که واریانس و میانگین را مجهول در نظر میگیرد آنگاه مقادیری را به آنها نسبت میدهد که با توجه به اطلاعات موجود محتملترین حالت باشد. در حالت کلی روش MLE در مورد یک مجموعهٔ مشخص از دادهها عبارتست از نسبت دادن مقادیری به پارامترهای مدل که در نتیجهٔ ان توزیعی تولید شود که بیشترین احتمال را به دادههای مشاهده شده نسبت دهد (یعنی مقادیری از پارامتر که تابع درستنمایی را حداکثر کند). MLE یک سازو کار مشخص را برای تخمین ارائه میدهد که در مورد توزیع نرمال و بسیاری توزیعهای دیگر بهطور خوشتعریف عمل میکند. با این حال در بعضی موارد مشکلاتی پیش میآید از قبیل اینکه برآوردگرهای حداکثر درستنمایی نامناسب اند یا اصلاً وجود ندارند.[2]
اصول
فرض کنید مشاهدهٔ زیر را داشته باشیم که بهطور مستقل از هم و یکنواخت توزیع شده و از یک توزیع با تابع توزیع احتمال نامشخص ƒ۰ پیروی میکنند. ƒ۰ بهطور محتمل متعلق به یک خانواده مشخص از توزیعهای نرمال مانند میباشد که مدل پارامتری نامیده میشود بنابراین . مقدار نامعلوم است و به عنوان مقدار صحیح پارامتر در نظر گرفته میشود. حال میخواهیم برآورد گری چون بیابیم که تا حد امکان به مقدار صحیح یعنی نزدیک باشد. هم xiها و هم پارامتر θ هر دو میتوانند بردار هم باشند. برای استفاده از روش درستنمایی بیشینه ابتدا باید تابع چگالی توام را برای همهٔ مشاهدات مشخص کنیم. برای حالتی که توزیعها مستقل و یکنواخت اند این تابع چگالی توام به صورت زیر است:
حال میخواهیم از زاویهای متفاوت به این تابع نگاه کنیم: فرض کنید مشاهدات پارامترهای ثابت و پارامتر متغیر این تابع باشد از این منظر این تابع، توزیع تابع درستنمایی نامیده میشود. در عمل بسیار راحتتر است که با لگاریتم تابع درستنمایی کار کنیم:
که لگاریتم درستنمایی نامیده میشود. یا نمونهٔ تراز شده اش که میانگین درستنمایی لگاریتمی نامیده میشود:
علامت هت بالای نشان دهندهٔ انست که ان وابسته به یک براوردگر میباشد. در واقع مقدار لگاریتم درستنمایی انتظاری یک مشاهدهٔ منفرد را در مدل بیان میکند. روش درستنمایی بیشینه را با یافتن مقداری از که را بیشینه کند تخمین میزند. این روش تخمین یک تقریب درستنمایی بیشینه از میباشد:
در این روش تفاوتی نمیکند که تابع درستنمایی را بیشینه کنیم یا لگاریتم درستنمایی را زیرا لگاریتم یک تبدیل یکنوا است. برای بسیاری از مدلها میتوان MLE را به صورت تابعی صریح از دادههای مشاهده شدهٔ x۱، …، xn پیدا کرد. اما در بسیاری از مسایل پیدا کردن یک فرم بسته برای تابع درستنمایی ممکن نیست و باید از روشهای عددی برای یافتن MLE استفاده کرد. برای برخی مسایل ممکن است تقریبهایی متفاوت موجود باشند که تابع را بیشینه کنند و برای برخی دیگر نیز هیچ تقریب مناسبی وجود ندارد. در گفتههای فوق فرض بر این بود که دادهها یه طور مستقل و یکنواخت توزیع شدهاند. اما این روش را میتوان به حوزههای وسیع تری نیز گسترش داد. در مسایلی پیچیدهتر چون سریهای زمانی حتی فرض استقلال هم میتواند حذف شود.
یک براوردگر درستنمایی بیشینه با یک براوردگر بیزی احتمال حداکثر که روی پارامترها یک توزیع پیشینی یکنواخت را میدهد منطبق است.
در مطالب فوق فرض بر این است که دادهها مستقل و دارای توزیع یکسان هستند. این روش میتواند برای حالتهای بیشتر از جمله نوشتن تابع چگالی مشترک (f (x1, … , xn | θ (پارامتر θ محدود و مستقل از سایز نمونهها n) و در یک فرمت سادهتر برای دادههای ناهمگون با تابع چگالی مشترک (f1 (x1 | θ) ·f2(x2|θ) · ··· · fn(xn | θ استفاده کرد. فرض میکنیم که هر نمونه مشاهده شده xi قابل استخراج از یک متغیر تصادفی با تابع توزیع fi باشد. در حالتهای پیچیده تری مانند سریهای زمانی، فرض مستقل بودن متغیرهای تصادفی میتواند راهگشا باشد.
برآورد درست نمایی بیشته در کنار برآورد بیزی با شرط داشتن یک توزیع یکنواخت بر روی پارامترها استفاده میشود. در واقع هرچه برآورد موخره بیشینه شود، احتمال پارامتر θمشروط به دادههای x۱، …، xn افزایش مییابد.
که در آن توزیع مقدم برای پارامتر θ است که در آن احتمال متوسط دادهها بر روی همه پارامترها ست. از آنجا که مخرج مستقل از θاست، برآوردگر بیزی ار بیشینه کردن رابطه بدست میآید. علاوه بر این فرض اگر در نظر بگیریم که احتمال مقدم توزیع یکنواخت دارد، تخمینگر بیزی از بیشینه کردن تابع درست نمایی بیشتر فرض کنیم که قبل از یک توزیع یکنواخت از بیزی برآورد به دست آمدهاست توسط به حداکثر رساندن احتمال تابع بدست میآید؛ بنابراین برآوردگر بیزی، برآورد درست نمایی بیشینه را با در نظر گرفتن توزیع مقدم یکنواخت همراهی میکند.
ویژگیها
درستنمایی بیشینه یک براوردگر اکسترمم بنا شده بر تابع هدف زیر میباشد
و مشابه نمونهای اش درستنمایی لگاریتمی میانگین ، میباشد. مقدار انتظاری اینجا متناظر با چگالی صحیح f(·|θ۰) محاسبه شود.
براوردگر درستنمایی بیشینه اساساً هیچگونه ویژگیهای بهینه برای نمونههای متناهی ندارد. با این حال این روش مشابه دیگر روشهای تخمین، برای بیان بسیاری از مسایل دارای ویژگیهای مجانبی جالبی میباشند که عبارتند از:
- سازگاری (برآوردگر سازگار): دنباله براوردهای درست نمایی بیشینه در احتمال، به مقدار تخمین زده شده همگرا است.
- نرمال مجانبی: متناظر با افزایش اندازهٔ نمونه توزیع MLE به یک توزیع گاوسی میل میکند که میانگین آن و ماتریس کوواریانس ان برابر است با وارون ماتریس اطلاعات فیشر.
- کارایی: زمانی که اندازهٔ نمونه به بینهایت میل میکند، برآورد به کران پایین کرامر-رائو برسد. این بدین معنی است که هیچ براوردگر مجانبی نااریبی خطای مربعی شدهٔ میانگین مجانبی کمتر از MLE ندارد.
- کارایی مرتبه دوم بعد از تصحیح برای اریب بودن
سازگاری
تحت شرایط مشخص شده در زیر، برآورد درست نمایی بیشینه سازگار است. اصولاً سازگاری به این معناست که با داشتن تعداد نمونه مشاهدات به اندازه کافی زیاد، میتوان مقدار را با دقت دلخواه پیدا کرد. به زبان ریاضی به این معنا است که اگر تعداد مشاهدات n به سمت بینهایت میل کند، در احتمال به مقدار واقعی اش همگرا میشود.
برای بیان سازگاری شروط ریز کافی است:
- شناسایی مدل
به عبارت دیگر مقادیر مختلف θ متناظر با توزیعهای مختلف در مدل است. اگر این شرط برقرار نباشد، آنگاه وجود دارد که و هردو مرتبط با یک توزیع از داده مشاهده شده میباشند. در اینصورت قادر به تمایز میان این دو پارامتر نخواهیم بود حتی اگر تعداد نمونههای مشاهده شده محدود باشد. در این حالت پارامترها به صورت مشاهدهای هم ارزند.
شرط شناسایی برای برآوردکننده درست نمایی بیشینه شرط لازم است. وقتی این شرط برقرار است تابع درست نمایی حدی یک مقدار بیشینه سراسری خواهد داشت.
- فشردگی
فضای پارامترهای مدل فشرده آیت.
شرط شناسایی بیانگر این بود که لگاریتم درست نمایی یک مقدار بیشینه سراسری دارد. فشردگی بیانگر این است که درست نمایی نمیتواند با شروع از یک نقطه دلخواه به مقدار بیشینه نزدیک شود.
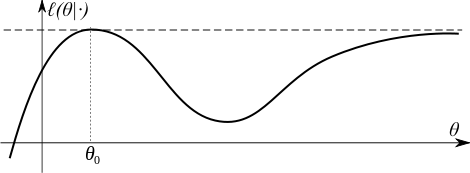
فشردگی صرفاً یک شرط کافی است و شرط لازم نیست. فشردگی میتواند با شروط دیگری از جمله شروط زیر جایگزین شود:
- فرورفتگیها در تابع لگاریتم درست نمایی و فشردگی آنها نسبت به مجموعه سطح تابع لگاریتم درست نمایی بالاتر باشد، یا
- وجود همسایگی فشرده N برای بهطوریکه خارج از همسایگی، تابع لگاریتم درست نمایی به اندازه ε>۰ از بیشینه مقدار، کمتر باشد.
- پیوستگی
تابع نسبت به θ برای تقریباً همه مقادیر x پیوسته باشد.
پیوستگی در اینجا میتواند با شرط ضعیف تر نیمه پیوستگی جایگزین شود.
- تسلط
با توجه به توزیع ، وجود دارد که:
for all
طبق قانون اعداد بزرگ، با تلفیق شرط تسلط و پیوستگی برای لگاریتم درست نمایی داریم:
شرط تسلط میتواند در مشاهدات متغیرهای تصادفی مستقل با توزیع یکسان استفاده شود. در مشاهدههای غیر مستقل با توزیع متفاوت، همگرایی یکنواخت در احتمال را میتوان با نشان دادن اینکه دنباله یک فرایند پیوسته - مساوی تصادفی است، بدست آورد.
نرمال مجانبی
در بسیاری از موارد، پارامترهای درست نمایی بیشینه، نرمال مجانبی را تخمین میزنند که برابر است با مجموعه پارامترهای صحیح و واقعی و خطای تصادفی که تقریباً نرمال است (البته با این فرض که دادهها کافی باشد)، و خطا با نرخ کاهش مییابد. برای اینکه این ویژگی برقرار باشد لازم است که برآوردکننده متحمل موضوعات زیر نباشد:
برآورد مرزی
گاهی برآورد درست نمایی بیشینه در کران مجموعه پارامترهای ممکن نهفتهاست یا درست نمایی بزرگ و بزرگتر میشود تا پارامترها به کران نزدیک شوند. تئوری مجانب استاندارد نیاز به این فرض دارد که پارامترهای واقعی دورتر از مرزها و کرانها قرار دارد. اگر دادههای کافی داشته باشیم، برآورد درست نمایی بیشینه از مرز دور نگه داشته میشود؛ ولی با تعداد نمونههای کمتر، برآورد به مرزها میرسد. در این موارد تئوری مجانبی تقریب کاربردی و درستی نمیدهد. مثالها در این موضوع مدلهای واریانس مؤلفهای هستند که هر مؤلفه دارای واریانس است که .
دادههای مرزی وابسته یه پارامتر
برای کاربردی کردن تئوری با یک روش ساده، مجموعهای از دادهها با احتمال مثبت را در نظر میگیریم که مستقل از پارامتر باشد. مثال سادهای که وابستگی به پارامترها در آن برقرار باشد تخمین زدن θ از مجموعهای مشاهدات مستقل با توزیع یکسان مانند توزیع یکنواخت در بازه است. برای برآورد بازههایی از θ را هدف میگیریم که در آن θ کمتر از مقدار بزرگترین مشاهده نباشد. چرا که بازه فشرده نیست، مقدار بیشینه برای تابع درست نمایی وجود ندارد. برای هر تخمینی از θ تخمین بزرگتری وجود دارد که درست نمایی بزرگتری دارد. به عکس، بازه شامل نقطه نهایی θ است و فشردهاست. در این موارد برآورد درست نمایی بیشینه وجود دارد که بایاس است. به صورت مجانبی، برآوردکننده درست نمایی بیشینه توزیع نرمال ندارد.
پارامترهای مزاحم
برای برآورد درست نمایی بیشینه، یک مدل ممکن است پارامترهای مزاحم داشته باشد. برای برقراری رفتار مجانبی، تعداد اینگونه پارامترها نباید با تعداد مشاهدات (سایز داده) افزایش یابد. یک مثال شناخته شده از این مورد وقتی است که مشاهدات به صورت جفتی رخ دهد که مشاهدات در هر جفت میانگینها مجزا و مجهول دارند ولیکن مستقل و دارای توزیع نرمال با یک واریانس مشترک هستند؛ بنابراین برای تعداد N مشاهده، تعداد پارامترها 2N+۱ خواهد بود. همانطور که میدانیم برآورد درست نمایی بیشینه برای واریانس به مقدار واقعی آن همگرا نمیشود.
افزایش اطلاعات
وقتی شرط مشاهدههای مستقل با توزیع یکسان برقرار نباشد، برای برقراری مجانب، نیازمندی اساسی این است که اطلاعات در دادهها با افزایش سایز نمونهها به صورت بینهایت افزایش یابد. این نیازمندی در شرایطی که وابستگی بین دادهها وجود داشته باشد و مشاهدات جدید مستقل باعث افزایش خطای مشاهدات شود، ارضا نمیشود.
از جمله شرایطی که این رفتار را تضمین میکند میتوان به موارد زیر اشاره کرد:
- مشتق مرتبه اول و دوم تابع لگاریتمی درست نمایی وجود داشته باشد
- ماتریس اطلاعات فیشر ماتریس وارون باشد
- ماتریس اطلاعات فیشر به عنوان یک تابع با پارامتر θ پیوسته باشد
- برآورد درست نمایی بیشینه سازگار باشد.
فرض کنید که شرایط سازگار بودن برآورد درست نمایی بیشینه برقرار باشد و
- و برای همسایگی N از از دو طرف پیوسته و مشتق پذیر باشد
- و
- وجود داشته باشد و غیر سینگولار باشد.
در اینصورت برآورد درست نمایی بیشینه به صورت مجانبی از توزیع نرمال پیروی میکند.
.
تغییرناپذیری کاربردی
برآوردکننده درست نمایی بیشینه مقادیری برای پارامتر انتخاب میکند که منجر به بزرگترین مقدار ممکن برای احتمال یک داده مشاهده شود. اگر پارامتر شامل تعدادی مؤلفه باشد، آنگاه برآوردگرهای درست نمایی بیشینه متفاوت برای آنها تعریف میکنیم. اگر برآورد درست نمایی بیشینه برای θ باشد و اگر تابع انتقال دلخواه θ باشد، آنگاه برآورد درست نمایی بیشینه برای از تعریف زیر بدست میآید:
که تابع درستنمایی را بیشینه میکند:
همچنین برآورد درست نمایی بیشینه نسبت به انتقال دادهها تغییرناپذیر است. اگر که یک به یک باشد و وابسته یه پارامتری که قرار است برآورد شود نباشد، آنگاه تابع چگالی در رابطه زیر صدق میکند:
تابع درست نمایی برای X و Y صرفاً در یک فاکتور تفاوت دارد که وابسته به پارامترهای مدل نیست.
برای مثال، پارامترهای برآورد درست نمایی بیشینهٔ توزیع لگاریتم درست نمایی همان پارامترهای توزیع نرمال است که به لگاریتم دادهها فیت شدهاست.
ویژگیهای مرتبه بالاتر
بر طبق مجانب استاندارد، برآوردکننده درست نمایی بیشینه باید ببه کران پایین کرامر-رائو برسد؛ بنابراین:
که I ماتریس اطلاعات فیشر است:
بهطور خاص، این به این معناست که بایاس برآوردکننده درست نمایی بیشینه برابر با صفر تا حداکثر مرتبه است. وقتی عبارت مرتبههای بالاتر برای توسعه توزیع این برآوردکننده را در نظر میگیریم، به این نتیجه میرسیم که یک بایاس از مرتبه دارد. بایاس برابر است با:
که براساس قرارداد جمعزنی اینشتین بر روی اندیسهای تکرار شونده ، یعنی j,k -امین مؤلفه وارون ماتریس اطلاعات فیشر ، و
با استفاده از این فرمولها میتوان بایاس مرتبه دوم برآوردکننده درست نمایی بیشینه را تخمین زد و هر بار با استفاده از بایاس آن را اصلاح کرد:
.
مثال
توزیع یکنواخت گسسته
توزیع گسسته، فضای نمونه متناهی
فرض کنید کسی میخواهد مشخص کند که یک سکه چگونه پشت یا رو میآید (با چه احتمالاتی) فرض کنید احتمال رو آمدن P باشد. هدف تعیین P است.
فرض کنید سکه ۸۰ بار پرتاب شده باشد، نمونه ممکن است چیزی شبیه این باشد: x۱ = H, x۲ = T , … , x۸۰ = T
احتمال پشت آمدن ۱ + p- است. فرض کنید نتیجه ۴۹ رو و ۳۱ پشت باشد و فرض کنید سکه از یک جعبه برداشته شود: یکی که احتمال رو آمدنش ۱/۳ است، یکی که احتمال رو آمدنش ۱/۲ است و دیگری که احتمال رو آمدنش ۲/۳ است. بر چسب سکهها گم شدهاست. با استفاده از این روش میتوان سکهٔ با بیشترین احتمال رو آمدن را پیدا کرد. داریم:
توزیع گسسته، فضای نمونه پیوسته
حالا فرض کنید که فقط یک سکه داریم که احتمال آن میتواند بین صفر و یک باشد. برای بیشینه کردن تابع بیشترین بخت داریم:
و بیشینه کردن برای تمام مقادیر ممکن احتمال بین صفر و یک است.
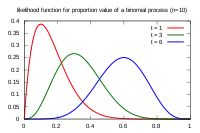
یک راه برای بیشینه کردن این تابع مشتقگیری نسبت به p و صفر قرار دادن آن است.
/
که دارای جواب p=۰ و p=۱ و p=۴۹/۸۰ است. جوابی که بخت را بیشینه میکند p=۴۹/۸۰ است؛ بنابراین بیشترین احتمال برای ۴۹/۸۰ است.
توزیع پیوسته، فضای نمونه پیوسته
برای توزیع نرمال که تابع چگالی احتمال آن به صورت زیر است:
تابع چگالی احتمال n متغیر تصادفی نرمال مستقل با توزیع یکسان به صورت زیر تعریف میشود:
به عبارت دیگر:
که در آن میانگین نمونهای است.
توزیع نرمال دارای دو پارامتر است : بنابراین درست نمایی را بر روی هر دو پارامتر به صورت همزمان یا در صورت امکان به صورت تک تک بیشینه میکنیم. از آنجا که تابع لگاریتم یک تابع پیوسته اکیداً صعودی است، مقداری که درست نمایی را ماکزیمم میکند، لگاریتم آن را هم ماکزیمم میکند. تابع لگاریتم درست نمایی را میتوان به صورت زیر نوشت:
مشتق لگاریتم درست نمایی را محاسبه میکنیم و آن را صفر قرار میدهیم:
که با عبارت زیر حل میشود:
که در واقع بیشینه تابع است چرا که صرفاً یک اکسترمم در μ وجود دارد و مشتق دوم اکیداً کمتر از صفر است؛ بنابراین امید آن برابر است با پارامتر μ.
که به این معنا است که برآوردکننده درست نمایی بیشینه بایاس نشدهاست.
علاوه بر این مشتق لگاریتم درست نمایی را نسبت به σ گرفته و مساوی صفر قرار میدهیم:
که جواب آن به صورت زیر است:
با قراردادن تخمین داریم:
برای محاسبه امید، آن را به فرم استاندارد با میانگین صفر بازنویسی میکنیم؛ بنابراین داریم:
با ساده کردن رابطه بالا با استفاده از دو رابطه و خواهیم داشت:
که به این معنا است که برآوردکننده بایاس و سازگار است.
میتوان گفت برآوردکننده درست نمایی بیشینه برای برابر است با:
در این مورد، براوردهای درست نمایی بیشینه میتوانند به صورت تک به تک و در حالت کلی ممکن است این براوردها به صورت همزمان بدست آیند.
فرم نرمال لگاریتمی درست نمایی در حالت بیشینه خود به صورت زیر است:
میتوان نشان داد که لگاریتم درست نمایی بیشینه در حالت کلی برا ی کمترین مربعات و برای کمترین مربعات غیر خطی یکی است. این موضوع میتواند برای تخمینهای مبتنی بر درست نمایی بازه اطمینان و منطقه اطمینان استفاده شود که در حالت کلی بسیار دقیق تر از استفاده از نرمال مجانبی که در بالا بحث شد، است.
متغیرهای غیرمستقل
در برخی موارد متغیرها همبسته هستند ولی مستقل نیستند. دو متغیر تصادفی X و Y مستقل هستند اگر و فقط اگر تابع چگالی احتمال مشترک آن دو، برابر با حاصلضرب تابع چگالی احتمال هر یک باشد. یعنی:
فرض کنید بردار تصادفی n بعدی از توزیع گوسی داشته باشیم که هر کدام از متغیرهای تصادفی دارای میانگین به صورت باشند. همچنین ماتریس کوواریانس را هم با نشان میدهیم.
تابع چگالی احتمال مشترک برای n متغیر تصادفی را با رابطه زیر نشان میدهیم:
در حالت دو متغیره تابع چگالی احتمال مشترک به صورت زیر است:
در این مورد و در دیگر موارد که تابع چگالی مشترک وجود داشته باشد، تابع درست نمایی که که در بالاتر و در بخش اصول تعریف شد از این چگالی استفاده میکند.
روالهای تکراری
مسئلهای را در نظر بگیرید که باید در آن هم حالت (وضعیت)های و هم پارامترهایی مانند تخمین زده شود. روالهای تکراری مانند الگوریتم امید ریاضی–بیشینه کردن روش حل برآورد پارامترها و وضعیتها است.
برای مثال، فرض کنید که n نمونه از وضعیتها که میانگین نمونه آن است با روشی مانند فیلتر کالمان و با استفاده از برآورد واریانس تخمین زده شده . سپس واریانس بعدی از محاسبه برآورد درست نمایی بیشینه و به صورت تکراری بدست میآید:
همگرایی برآورد درست نمایی بیشینه در روشهای فیلترینگ و هموار سازی در مقالات متعددی مورد مطالعه قرار گرفته شدهاست.
جستارهای وابسته
منابع
- Hendry, David F.; Nielsen, Bent (2007). Econometric Modeling: A Likelihood Approach. Princeton: Princeton University Press. ISBN 978-0-691-13128-3.
- Rossi, Richard J. (2018). Mathematical Statistics: An Introduction to Likelihood Based Inference. New York: John Wiley & Sons. p. 227. ISBN 978-1-118-77104-4.
