ناهمواریانسی
در آمار دنبالهای، متغیرهای تصادفی که دارای واریانسهای متفاوتی باشد ناهمواریانس (heteroscedastic) نامیده میشود. در مقابل به یک دنباله از متغیرهای تصادفی واریانس همسان میگویند اگر دارای واریانس ثابتی باشند.
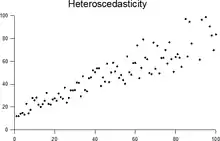
فرض کنیم یک دنباله از متغیرهای تصادفی در اختیار داریم:.{Yt}t=۱n . ویک دنباله از بردارهای متغیرهای تصادفی:.{Xt}t=۱n. با استفاده از امید ریاضیYt. به شرط Xt. دنباله ی.{Yt}t=۱n. واریانس ناهمسان نامیده میشود اگر واریانس Yt به شرط Xtبا تغییر t تغییر نماید. برخی از منابع از این تعریف تحت عنوان “واریانس ناهمسانی مشروط “یاد میکنند، که این موضوع جهت تأکید بر این واقعیت است که «دنبالهای از واریانسهای شرطی» میباشند که متفاوت بوده و تغییر مییابند و نه واریانسهای غیر شرطی. در واقع ممکن است واریانس ناهمسانی مشروط داشته باشیم در حالی که متغیرهای تصادفی بهشکل غیر شرطی واریانس همساناند. باید توجه داشت عکس این موضوع صادق نمیباشد. وقتی که از روشهای آماری از قبیل روش حداقل مربعات جهت برآوردهای آماری استفاده مینماییم تعدادی از فروض را به شکل ضمنی لحاظ نمودهایم. یکی از این فروض این است که جملات خطا دارای واریانس یکساناند. حتی اگر فرض کنیم که جملات خطا متعلق به توزیعهای آماری مشابهی باشند این فرض ممکن است صحیح نباشد. برای مثال جملات خطا میتوانند به ازای هر مشاهده تغییر یافته و فرضاً افزایش یابند. این مسئله برای مشاهداتی که از دادههای مقطعی بدست آمدهاند کاملاً رایج است. واریانس ناهمسانی عموماً به عنوان یکی از موضوعات مورد بحث در اقتصادسنجی شناخته میشود. در میان اقتصادسنجیدانها رابرت انگل در سال ۲۰۰۳ بخاطر مطالعاتی که پیرامون تحلیل رگرسیون با فرض وجود واریانس ناهمسانی داشت موفق به کسب جایزهٔ نوبل گردید. حاصل مطالعات وی روشی جهت تخمین رگرسیون در شرایط واریانس ناهمسانی حاصل نمود که تحت عنوان روش مدلسازی آرک ARCH شناخته میشود.
نتایج
بایستی توجه داشت که با وجود مشکل واریانس ناهمسانی برآوردهای ما از ضرایب به کمک روش حداقل مربعات همچنان بدون تورش باقی میماند. اما واریانس برآورد شده با روش حداقل مربعات برای ضرایب در این شرایط تورش دار خواهد بود؛ یعنی در این شرایط واریانس برآوردی ضرایب مقادیری بیشتر یا کمتر از واریانس حقیقی جامعه را ارائه میدهد. از اینرو استنتاجهایی که به روش حداقل مربعات در این شرایط صورت میگیرد ممکن است صحیح نباشد. به عنوان مثال فرض کنیم واریانس برآورد شده مقداری کوچکتر از واریانس جامعه را ارائه دهد در این صورت مقداری که برای آمارهٔ تی محاسبه میشود مقدار بزرگتری از مقدار واقعی آماره را نمایان میسازد و این امکان را ایجاد میکند که بهشکل غیرواقعی مقدار آماره در ناحیهٔ بحرانی قرار بگیرد. و از اینرو فرضیه صفر که دلالت بر معنادار نبودن ضریب برآورد شده دارد رد میگردد، حال آنکه ممکن است ضریب مذکور بی معنا بوده باشد. از دیگر نتایجی که واریانس ناهمسانی بهمراه دارد عدم اعتبار فاصلهٔ اطمینان میباشد. از آنجا که برآورد صحیحی از واریانس نداریم طبیعتاً فاصلهٔ اطمینان نیز که بر اساس این واریانس ساخته میشود قابل اعتماد نیست. همچنین در این شرایط آزمونهای معنا داری ضرایب همانند آزمون اف یا آزمون ال-ام نتایج صحیحی را حاصل نمیکنند.
روشهای شناسایی واریانس ناهمسانی
آزمونهایی جهت شناسایی مشکل واریانس ناهمسانی پیشنهاد شدهاند از جمله: آزمون پارک، آزمون گلچسر، آزمون وایت، آزمون بروش-پاگان، آزمون گلدفلد-کوانت روشی که معمولاً در این آزمونها از آن بهره گرفته میشود استفاده از یک رگرسیون کمکی است. به این ترتیب که پس از برآورد مدل جملات پسماند (به عنوان نزدیکترین متغیری که میتواند جملات خطا را نمایندگی نماید) استخراج شده ومجذور آنها روی متغیرهای توضیح دهندهٔ مدل رگرس میگردد در صورتی که رگرسیون حاصل بهطور کلی معنا دار باشد شاهدی بر وجود واریانس ناهمسانی خواهد بود.
رفع واریانس ناهمسانی
- استفاده از روش حداقل مربعات تعمیم یافته به جای روش حداقل مربعات معمولی. (استفاده از این روش مستلزم شناسایی شکل واریانس ناهمسانی و متغیر توضیح دهنده ایست که مشکل را ایجاد کردهاست)
- بازنگری در تصریح مدل
- استفاده از مقادیر لگاریتمی متغیر توضیح دهنده به جای مقادیر سادهٔ آن متغیر.
- استفاده از برآورد همسان انحراف معیار وایت.
نمونههایی از واریانس ناهمسانی
در غالب پدیدههای انسانی و اجتماعی شاهد یک فرایند یادگیری میباشیم به این معنی که افراد بر اساس تجربههای گذشته خود رفتارهای آتی را اصلاح مینمایند این ویژگی میتواند ایجاد واریانس نا همسانی نماید. یک مثال متداول از این موضوع بررسی رابطهٔ بین میزان خطا و ساعات تمرین میباشد طبیعی است اگر انتظار داشته باشیم در ساعات اولیهٔ تمرین یک فعل افراد بنا بر استعدادهای متفاوتی که دارند میزان خطای کاملاً متفاوتی دارند اما با افزایش ساعات تمرین از دامنهٔ خطا کاسته میشود.
بعنوان مثالی دیگر میتوان به تفاوت در واریانس سطح مصرف بر اساس سطوح مختلف درآمدی در یک مجموعه داده مقطعی اشاره نمود. معمولاً در در آمدهای پایین افراد انتخابهای مصرفی چندان متنوعی نداشته و دامنهٔ نوسان در مصرف محدود است اما بهتدریج که به مشاهدات با در آمدهای بالا میرسیم دامنه نوسان در مصرف افزایش مییابد.
