قانون اعداد بزرگ
قانون اعداد بزرگ احتمالاً معروفترین نتیجه در نظریهٔ احتمالات است که برای توصیف نتیجهٔ تکرار یک آزمایش به دفعات زیاد به کار میرود. بر طبق این قانون هر قدر تعداد دفعات تکرار آزمایش بیشتر شود، میانگین نتایج به امید ریاضی آن نزدیکتر میشود.[1]
| بخشی از مجموعه مباحث درباره آمار |
| نظریهٔ احتمالات |
|---|
 |
| اصول احتمال |
| فضای احتمالی (en) * فضای نمونه * پیشامد ابتدایی (en) * پیشامد * اندازه احتمالاتی (en) |
| پیشامد مکمل (en) * توزیع احتمال توأم * توزیع حاشیهای (en) * احتمال شرطی |
| متغیرهای تصادفی مستقل * استقلال شرطی (en) * قانون احتمال کامل * قانون اعداد بزرگ * قضیه بیز * نابرابری بول (en) |
| نمودار ون * نمودار درختی |
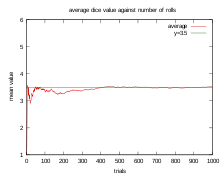
به عنوان یک مثال، وقتی یک تاس ششوجهی را یک بار بریزیم، یکی از عددهای ۱، ۲، ۳، ۴، ۵ یا ۶ به دست خواهد آمد. اگر این آزمایش را تکرار کنیم، هر دفعه یکی از این اعداد به دست میآیند و اگر تاس نااریب باشد، احتمال دیده شدن این اعداد با هم برابر است. در نتیجه امید ریاضی عددی که با ریختن هر بار تاس به دست میآید طبق این فرمول:
برابر با ۳٫۵ است. طبق قانون اعداد بزرگ، هرگاه آزمایش ریختن تاس را به دفعات زیاد تکرار کنیم، میانگین اعدادی که به دست میآید تدریجاً به ۳٫۵ نزدیک خواهد شد.[2] بهطور مثال میتوان به آزمایش پرتاب سکه اشاره کرد. همانطور که میدانیم نتیجه این آزمایش توزیع برنولی دارد. اگر فقط یک بار آزمایش را انجام دهیم احتمال رو آمدن سکه برابر ۱/۲ است، طبق قانون اعداد بزرگ اگر تعداد پرتابها زیاد باشد نسبت تعداد رو آمدنها به تعداد کل پرتابها به ۱/۲ میل میکند[2] مشخص است که اختلاف تعداد روها و پشتها با زیاد شدن تعداد آزمایشها افزایش پیدا میکند. پس احتمال کوچک بودن اختلاف روها و پشتها به سمت عدد صفر میل میکند. هم چنین میتوان نتیجه گرفت که نسبت اختلاف روها و پشتها به تعداد کل پرتابها نیز به سمت صفر میروند. از این حقیقت در مییابیم که با وجود رشد اختلاف بین تعداد روها و پشتها در انجام این آزمایش به دفعات زیاد، سرعت این رشد از سرعت افزایش تعداد کل پرتابها کمتر است.[2]
- میتوان قانون اعداد بزرگ را به صورت خلاصه شده به شکل زیر نوشت:
که در آن دنبالهای از متغیرهای تصادفی مستقل با توزیع یکسان و میانگین هستند.
(Gerolamo Cardano (۱۵۰۱–۱۵۷۶ جیرولامو کاردانو ریاضیدان ایتالیایی بدون اثبات ریاضی بر این باور بود که دقت نتایج تجربی در امار با افزایش تعداد دفعات آزمایش بیشتر میشود[4] این فرضیه بعدها تحت عنوان قانون اعداد بزرگ اثبات شد و مورد توجه قرار گرفت. حالت خاصی از این قانون برای متغیرهای برنولی برای نخستین بر توسط Jacob Bernoulli ژاکوب برنولی اثبات شد.[5] او این قانون را قضیه طلایی نامید، ولی بعدها با نام قانون اعداد بزرگ مشهور شد. در سال ۱۸۳۵ سیمون دنیز پواسون Siméon Denis Poisson این قانون را با نام قانون اعداد بزرگ توضیح داد. هماکنون این قضیه با هر دو نام ذکر شده شناخته میشود.[6] بعد از برنولی و پواسون ریاضیدانان دیگری مانند مارکف، چبیشف، بورل و کولموگرف برای بهبود این تعریف و اثبات آن تلاش کردند و در نهایت الکساندر کینچین برای هر متغیر تصادفی دلخواه آن را اثبات کرد. این تلاشها منجر به پیدایش دو حالت مختلف از این قانون شد. این دو قسمت عبارت است از قانون ضعیف و قوی. قانون ضعیف و قوی اعداد بزرگ دو قانون متفاوت نیستند. در بلکه این دو قانون از دو دیدگاه متفاوت موضوع همگرایی احتمال وقتی تعداد دفعات آزمایش زیاد است به مقدار میانگین را توضیح میدهند. همچنین میتوان قانون ضعیف را از قانون قوی نتیجه گرفت.[7]
گفتنی است نصرا... اعتمادی (1324 ش - ...)(1945 م - ...) احتمال دان ایرانی اثباتی بدیغ برای قانون اعداد بزرگ در سال 1981 م ارائه داد که هم اکنون در بسیاری از کتابهای نظریه احتمال مانند کتاب P. Billingsley) Probability and Measure) درج شده است. در این اثبات، شرط استقلال توام متغیرهای تصادفی به شرط استقلال دو به دو کاهش یافته است و افزون اینکه از شیوه ای بدیع در اثبات استفاده شده است.
منابع
- Introduction to Probability Models,Sheldon M.Ross,tenth edition
- http://en.wikipedia.org/w/index.php?title=Law_of_large_numbers&oldid=437185925
- شلدون راس، "مبانی احتمال" مترجمین: دکتر احمد پارسیان و دکتر علی همدانی
- Mlodinow, L. The Drunkard's Walk. New York: Random House, 2008. p. 50.
- Jakob Bernoulli, Ars Conjectandi: Usum & Applicationem Praecedentis Doctrinae in Civilibus, Moralibus & Oeconomicis, 1713, Chapter 4, (Translated into English by Oscar Sheynin)
- Hacking, Ian. (1983) "19th-century Cracks in the Concept of Determinism"
- http://en.wikipedia.org/w/index.php?title=Probability_theory&action
