تابع Càdlàg

در ریاضیات یک تابع càdlàg یا corlol تابعی است که روی اعداد حقیقی یا زیرمجموعه‌ای از آن تعریف می‌شود به صورتی که همه جا از راست پیوسته است و از چپ دارای حد (ریاضی) است. توابع càdlàg در مطالعهٔ فرایندهای تصادفی اهمیت دارند به گونه‌ای که برخلاف حرکت براونی که مسیر نمونه‌هایی پیوسته دارد ، نا پیوستگی را در مسیرهای نمونه‌ای قابل قبول می‌داند. مجموعه توابع càdlàg روی یک دامنه به عنوان فضای Skorokhod شناخته می‌شود.

دو اصطلاح مرتبط عبارتند ازcàglàd برای بیان càdlàg چپ-راست بازگشتی و càllàl برای تابعی که روی هر نقطه‌ای از دامنه به هر دو صورتcàdlàg یا càglàd قابل معاوضه است.

تعریف

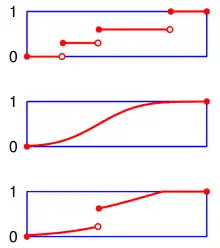
توزیع تجمعی توابع نمونه‌هایی از توابع càdlàg .

فرض کنید (M, d) یک فضای متریک و همچنین E ⊆ R باشد. یک تابع ƒ: E → M ،تابع càdlàg نامیده می‌شود اگر برای هر t ∈ E:

حد چپ (ƒ(t−) := lims↑t ƒ(s وجود داشته باشد، و
حد راست موجود (ƒ(t+) := lims↓t ƒ(s و برابر (ƒ(t باشد.

که این بدان معناست که ƒ از راست پیوستگی و از چپ حد دارد.

نمونه‌ها

تمام توابع پیوسته ، càdlàg هستند.
به عنوان یک نتیجه از تعریف توابع càdlàg ، تمام توابع توزیع تجمعی càdlàg هستند. برای نمونه احتمال تجمعی در نقطه ی r میزان احتمالی است که یک متغیر تصادفی کمتر یا بیشتر از r باشد ، $\mathbb {P} [x\leq r]$ .
مشتق راست $f_{+}^{\prime }$ هر تابع محدب f که روی یک بازهٔ باز تعریف شده باشد ،یک تابع cadlag افزایشی است.

فضای Skorokhod

مجموعهٔ تمام توابع càdlàg از E تا M اغلب به صورت (D(E; M (و یا برای سادگی D) نمایش داده می‌شود و فضای Skorokhod نامیده می‌شود. می‌توان به فضای Skorokhod یک توپولوژی نسبت داد که مستقیماً ما را قادر می‌سازد "فضا و زمان را قدری دگرگون سازیم" (درحالی که توپولوژی‌های سنتی مربوط به همگرایی یکنواخت تنها اجازهٔ دگرگونی اندک فضا را می‌دهد)

برای سادگی [E = [0, T و M = Rⁿ — برای بررسی بیشتر ساختار به Billingsley مراجعه کنید.

نخست لازم است که یک ماژول پیوستگی مشابه تعریف شود:

(ϖ′ƒ(δ .برای هر F ⊆ E، قرار دهید :

w_{f}(F):=\sup _{s,t\in F}|f(s)-f(t)|

و برای δ> 0 ماژول càdlàg را چنین تعریف کنید:

\varpi '_{f}(\delta ):=\inf _{\Pi }\max _{1\leq i\leq k}w_{f}([t_{i-1},t_{i})),

که در آن مقدار infimum روی تمام اجزای Π = {0 = t₀ <t₁ <… <t_k = T}, k ∈ N, با min_i (t_i − t_i−1)> δ محاسبه می‌شود. این شیوهٔ تعریف برای توابع غیر càdlàg شهودا پذیرفتنی است و می‌توان نشان داد که ƒ در اینجا càdlàg است اگر و تنها اگر ϖ′_ƒ(δ) → 0 جایی که δ → 0.

فرض کنید Λ مجموعه تمام توابع دوسویه پیوسته و strictly increasing از E به خودش باشد.(اینها "دگرگونی در زمان" هستند) فرض کنید:

\|f\|:=\sup _{t\in E}|f(t)|

نرم (ریاضی) یکنواخت روی تابع E را مشخص کند. متریک Skorokhod زوی σ در D به صورت زیر تعریف شود:

\sigma (f,g):=\inf _{\lambda \in \Lambda }\max\{\|\lambda -I\|,\|f-g\circ \lambda \|\},

که در آن I: E → E تابع همانی است. در بیان "wiggle" ، مقدار||λ − I|| برابر است با "wiggle در زمان" و ||ƒ − g○λ|| ااندازهٔ "wiggle در فضا" را مشخص می‌کند.

توپولوژی Σ تولید شده توسط σ توپولوژِی Skorokhod توپولوژی در Dاست.

خواص فضای Skorokhod

تعمیم توپولوژی یکنواخت

فضای C از توابع پیوسته E یک زیرفضا از D است. توپولوژی Skorokhod با C هم‌زمان با, توپولوژی وجود دارد.

کامل بودن

می توان نشان داد که، اگرچه D با معیار Skorokhod یک فضای کامل نیست ، یک معیار معادل توپولوژیکی σ₀ وجود دارد که D با توجه به آن کامل است.[1]

جدایی‌پذیری

با در نظر گرفتن هر کدام از σ یا σ₀، فضا ی D یک فضای تفکیک پذیر است بنابراین Skorokhod یک فضای polish است.

تنگی در فضای Skorokhod

به عنوان یک کاربرد از با قضیه Arzelà–Ascoli می‌تواند نشان داد که یک دنباله ,...μn)n=1,2) از اندازه‌گیری‌های احتمالاتی روی فضای D سخت است اگر و تنها اگر : $\lim _{a\to \infty }\limsup _{n\to \infty }\mu _{n}{\big (}\{f\in D\;|\;\|f\|\geq a\}{\big )}=0,$

و

$\lim _{\delta \to 0}\limsup _{n\to \infty }\mu _{n}{\big (}\{f\in D\;|\;\varpi '_{f}(\delta )\geq \varepsilon \}{\big )}=0{\text{ for all }}\varepsilon >0.$

ساختار جبری و توپولوژیکی

تحت توپولوژِی Skorokhod و جمع نقطه‌ای توابع ، D یک گروه توپولوژیکال نیست ، به عنوان مثال:

فرض کنید بازیهٔ واحد باشد و در نظر بگیرید که یک دنباله از توابع مشخصه باشد . برخلاف این واقعیت که در توپولوژی ، دنبالهٔ به 0 همگرا نمی‌شود.

منابع

Convergence of probability measures - Billingsley 1999.

https://en.wikipedia.org/wiki/Càdlàg

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Convergence of probability measures - Billingsley 1999.

فرایندهای تصادفی
فرایند تصادفی	فرایند برنولی فرایند شاخه‌ای فرایند رستوران چینی فرایند گالتون-واتسون متغیرهای تصادفی مستقل با توزیع یکسان زنجیره مارکوف فرایند مورن ولگشت Loop-erased ولگشت خودپرهیز (قدم زدن بدون قطع کردن خود)
Continuous time	Bessel process Birth–death process فرایند وینر Bridge Excursion Fractional Geometric Meander فرایند کوشی Contact process گام-تصادفی زمان-پیوسته Cox process Diffusion process Empirical process فرایند فلر فرایند فلمینگ-ویوت Gamma process Hunt process Interacting particle systems Itô diffusion فرایند ایتو Jump diffusion Jump process فرایند لوی Local time Markov additive process McKean–Vlasov process فرایند اورنستین-یولنبک فرایند پواسون Compound فرایند پواسون فرایند پواسون تحول شرام و لونر Semimartingale Sigma-martingale Stable process Superprocess Telegraph process Variance gamma process فرایند وینر Wiener sausage
Both	فرایند شاخه‌ای Galves–Löcherbach model فرایند گاوسی مدل پنهان مارکف زنجیره مارکوف مارتینگیل Differences Local مارتینگیل مارتینگیل Random dynamical system Regenerative process نظریه تجدید Stochastic chains with memory of variable length نویز سفید
Fields and other	فرایند دیریکله Gaussian random field Gibbs measure شبکه هاپفیلد مدل آیزینگ Potts model شبکه بولی میدان تصادفی مارکفی نظریه تراوش فرایند پیتمن-یور فرایند نقطه ای Cox فرایند پواسون میدان تصادفی گراف تصادفی
سری زمانی	واریانس ناهمسانی شرطی اتورگرسیو میانگین متحرک خودهمبسته یکپارچه مدل خودهمبسته مدل خودهمبسته میانگین متحرک واریانس ناهمسانی شرطی اتورگرسیو مدل میانگین متحرک
Financial models	مدل بلک-درمن-توی Black–Karasinski مدل بلک-شولز مدل چن Constant elasticity of variance (CEV) مدل کاکس-اینگرسول-راس Garman–Kohlhagen Heath–Jarrow–Morton (HJM) Heston Ho–Lee Hull–White LIBOR market Rendleman–Bartter SABR volatility مدل واسیچک Wilkie
بیمسنجی	Bühlmann Cramér–Lundberg Risk process Sparre–Anderson
نظریه صفs	Bulk Fluid Generalized queueing network M/G/1 صف M/M/1 M/M/c
Properties	تابع Càdlàg Continuous Continuous paths ارگادیسیتی متغیرهای تصادفی تعویض پذیر Feller-continuous فرآیندهای تصادفی گاوسی-مارکوف خاصیت مارکف Mixing Piecewise deterministic Predictable Progressively measurable Self-similar فرایند مانا Time-reversible
Limit theorems	قضیه حد مرکزی Donsker's theorem Doob's martingale convergence theorems نظریه ارگودیک Fisher–Tippett–Gnedenko theorem Large deviation principle قانون اعداد بزرگ قانون لگاریتم‌های تکراری Maximal ergodic theorem Sanov's theorem
Inequalities	Burkholder–Davis–Gundy Doob's martingale Kunita–Watanabe
Tools	Cameron–Martin formula همگرایی متغیرهای تصادفی Doléans-Dade exponential Doob decomposition theorem Doob–Meyer decomposition theorem Doob's optional stopping theorem Dynkin's formula Feynman–Kac formula Filtration Girsanov theorem Infinitesimal generator Itô integral Itô's lemma Kolmogorov continuity theorem Kolmogorov extension theorem Lévy–Prokhorov metric Malliavin calculus Martingale representation theorem Optional stopping theorem Prokhorov's theorem Quadratic variation Reflection principle Skorokhod integral Skorokhod's representation theorem تابع Càdlàg Snell envelope معادله دیفرانسیل تصادفی Tanaka زمان توقف Stratonovich integral Uniform integrability Usual hypotheses Wiener space Classical Abstract
Disciplines	بیمسنجی اقتصادسنجی نظریه ارگودیک نظریه مقدار حدی قضیه انحرافات بزرگ مالیه ریاضیاتی آمار ریاضی نظریه احتمالات نظریه صف نظریه تجدید Ruin theory آمار حسابان تصادفی سری زمانی یادگیری ماشین
List of topics