نظریه تراوش
در ریاضیات، نظریه تراوش به توضیح رفتار خوشهها در گرافهای تصادفی میپردازد. از کاربردهای نظریه تراوش میتوان در علم مواد و دیگر حوزههایی که در مورد نفوذ و تراوش مواد بحث میکنند استفاده کرد.
مقدمه
علت نامگذاری نظریه تراوش و سرآغاز آن این سؤال است، فرض کنید مایعی در بالای جسمی منفذدار ریخته شدهاست، آیا میتواند با گذر از منافذ این جسم خود را به سطح پایینی آن برساند؟ این سؤال که در دنیای واقعی و فیزیک مطرح میشود در ریاضیات به صورت شبکهٔ سه بعدی از n*n*n راس مدلسازی میشود، به هرکدام از این رئوس اتاقک هم گفته میشود، یال بین هر دو راس میتواند مستقل از بقیه یالها به احتمال p باز باشد (اجازه انتقال ماده را بدهد) یا به احتمال 1-p بسته باشد. در اینصورت برای هر p داده شده احتمال اینکه مسیری از یالهای باز از رئوس بالایی به رئوس پایینی وجود داشته باشد چقدر است؟ هدف اولیه این سؤال بررسی رفتار گراف برای nهای بزرگ میباشد.
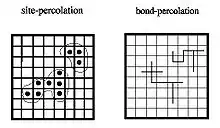
این مسئله که تراوش زنجیرهای نامیده میشود اولین بار در ریاضیات توسط Broadbent & Hamersley (1957) مطرح شده و تا به حال توسط تعدادی از فیزیکدانان و ریاضیدانان مشتاقانه دنبال شدهاست.
در مدلسازی دیگری با تفاوت کمی برای بدست آوردن گراف تصادفی، فرض میکنیم که هر کدام از اتاقکها به احتمال p «پر» و با احتمال ۱-p «خالی» هستند (یالها در این مدل حذف شدهاند). در این مسئله که تراوش اتاقکی نامیده میشود سؤال مانند قبل است: برای هر p داده شده احتمال اینکه مسیری از اتاقکهای پر از بالا به سطح پایینی وجود داشته باشد چقدر است؟
البته همین سؤالات را میتوان برای هر ابعادی از شبکه مطرح کرد. همانطور که واضح است، بررسی یک شبکه نامحدود نسبت به یک شبکه با ابعاد بزرگ سادهتر است. در این حالت سؤال بالا به این صورت در میآید: آیا خوشهٔ بازبینهایت وجود دارد؟ یا به عبارتی آیا در میان رأسهای متصل به هم مسیری به طول بینهایت در داخل شبکه وجود دارد؟ با توجه به قانون کولموگوروف،[* 1] برای هر p داده شده، احتمال اینکه چنین خوشهای وجود داشته باشد یا یک است یا صفر. از آنجایی که این احتمال تابعی صعودی از p است، یک نقطهٔ بحرانی از p وجود دارد (که با pc نشان داده میشود) که قبل از این نقطه به احتمال ۰ و بعد از آن به احتمال ۱ چنین مسیری وجود خواهد داشت. در عمل این تغییر فاز بحرانی به راحتی قابل مشاهده است. حتی اگر n به مانند ۱۰۰ کوچک هم باشد، احتمال اینکه مسیری از بالا به سطح پایینی وجود داشته باشد در بازهای نزدیک به pc از نزدیکیهای صفر تا نزدیکیهای یک به شدت افزایش مییابد.

در بعضی موارد pc بهطور مستقیم قابل محاسبه میباشد. برای مثال، در تراوش زنجیرهای در شبکه مربعی Z۲ و در دو بعد، pc=۱/۲ است که این مسئله برای مدت ۲۰ سال به صورت سؤالی حل نشده مانده بود و در نهایت نزدیکیهای سال ۱۹۸۰ توسط هری کستن[* 2] جوابی برای آن پیدا شد. حالت محدودی برای شبکهها در ابعاد بسیار توسط شبکه بته[* 3] داده شدهاست، که در آن آستانهٔ بحران برای عدد مختصاتی z در pc=1/(z-۱) میباشد. در بیشتر گرافهای شبکهای نامتناهی نمیتوان pc را به صورت دقیق تعیین کرد. برای مثال برای تراوش زنجیرهای در مکعبهای چند بعدی pc نامعلوم میباشد.
تمامیت
بنابر اصل تمامیت مقدار pc به ساختار گراف وابسته است؛ درحالی که رفتار خوشهها برای مقادیر pc، بیش از آن و کمتر از آن مستقل از ساختار گراف میباشد؛ بنابراین برای بررسی برخی مسائل کمیتهایی به جز pc، که مستقل از ساختار گراف هستند در نظر گرفته میشود. برای مثال برای بعدهای یکسان، بعد فراکتالی خوشهها برای pc برابر میباشد؛ و از نوع تراوش (برای مثال اتاقکی یا زنجیرهای) و نوع شبکهبندی مستقل است.
فازها
فازهای زیربحرانی و فوق بحرانی
ویژگی مهم فاز زیر بحرانی «فروپاشی نمایی» آن ااست. وقتی که p <pc است، احتمال اینکه نقطهای خاص که در خوشهٔ بازی به اندازه r قرار دارد فروپاشی کرده و اندازهاش خوشه صفر شود، متناسب با توان r است. این موضوع برای برای ترواش در بیش از دو بعد توسط Menshikov (1986) و بهطور جداگانه توسط Aizenman & Barsky (1987) اثبات شدهاست. برای ترواش در دو بعد نیز، حالتی از برهان Kesten میباشد. گراف یکریخت شبکه مربعی Z2، خود نیز شبکه مربعی میباشد؛ بنابراین، برای ترواش در دو بعد، فاز فوق بحرانی دوگان فرایند ترواش زیربحرنی است. مهمترین نتیجه در مورد فاز فوق بحرانی تراوش در بیش از دو بعد، این است که، برای N به اندازه کافی بزرگ، خوشه باز نامتناهی در صفحه دوبعدی Z2 × [0, N] وجود دارد. این موضوع را Grimmett & Marstrand (1990) ثابت کردهاند. در تراوش دو بعدی با p <1/2، با احتمال یک، خوشه بسته نامتناهی یکتا وجود دارد؛ بنابراین فاز زیربحرانی را میتوان به عنوان جزیره متناهی باز در یک قیانوس نامتناهی بسته در نظر گرفت. برای p <1/2، عکس حالت فوق رخ میدهد؛ فاز زیر بحرانی جزیره متناهی بسته در یک اقیانوس نامتناهی باز خواهد بود. برای بیش از دو بعد تصویر پیچیده خواهد بود. همچنین برای p بین pc و 1-pc خوشههای باز و بسته نمتناهی توامان وجود خواهند داشت.
فاز بحرانی
مدل تراوش در نقطه بحرانی p = pc دارای تکینگی نمایی میباشد. نظریه مقیاسبندی، برحسب ابعاد که نوع تکینگی را مشخص میکند؛ وجود نمای بحرانی را پیشبینی میکند. برای حالت دو بعدی این پیشبینی با نظریه کوانتم و جاذبه کوانتومی و مقادیر عددی بدست آمده همخوانی دارد. بیشتر این پیشبینیها به جز برای حالت دو بعدی و بیش از ۱۸ بعد تخمینی هستند. پیشبینیهای بیان میکنند که:
- هیچ خوشه بسته یا باز نامتناهی وجود ندارد.
- احتمال اینکه مسیر بازی به طول r از یک نقطه مشخص وجود داشته باشد، به صورت چند جملهای از O(rα) میباشد:
- بنابر اصل تمامیت α فقط به تعداد بعدها وابسته است.o بنابر اصل تمامیت α فقط به تعداد بعدها وابسته است.
انواع تراوش
تراوش برنولی که زنجیرهها مستقل از هم هستند. فیزیکدانها این تراوش، تراوش زنجیرهای مینامند. ترواش جهتدهی شده که با فرایند تصادفی contact process مرتبط هستند. تراوش برنولی بر روی گرافهای کامل نمونهای از گرافهای تصادفی هستند و احتمال بحرانی آنها p = 1/n میباشد.



