گراف (ریاضی)
گِراف یا نِگار در ریاضیات دستکم دارای دو معنی میباشد. در ریاضیات پایه گراف اشاره به نمودار تابع دارد، و در اصطلاح ریاضیدانان، گراف مجموعهای از نقاط و خطوط به هم پیوسته است.
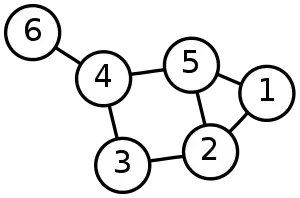
در واقع گراف مدلی ریاضی برای یک مجموعه گسسته است که اعضایش به گونهای با هم پیوند دارند. اعضای این مجموعه میتوانند چند انسان باشند و ارتباط میان آنها دست دادن با یکدیگر باشد. اعضا میتوانند اتمها در یک مولکول باشند و ارتباطشان پیوندهای شیمیایی باشد یا این که اعضا میتوانند بخشهای گوناگون یک زمین و ارتباط میانشان، پلهایی باشد که آنها را به هم میپیوندند (همانند مسئله کونیگسبرگ).[1]
نظریه گراف یکی از موضوعهای مهم در ریاضیات گسسته است که به شناخت گرافها و مدلبندی مسایل با آنها میپردازد. لئونارد اویلر در سال ۱۷۳۶ با حل مسئله پلهای کونیگسبرگ نظریهٔ گرافها را بنیان گذاشت. اما جیمز جوزف سیلوستر نخستین کسی بود که در سال ۱۸۷۸ این مدلهای ریاضی را گراف نامید.[2]
تعریف
گراف ساده: یک گراف از مجموعهای غیر خالی از اشیاء به نام رأس تشکیل شده، که آن را با نشان میدهیم، و مجموعهای شامل یالها، که رأسها را به هم وصل میکنند و با نمایش میدهیم. یک چنین گرافی را با نشان میدهیم. اگر یال دو رأس و را به هم وصل کند مینویسیم .[3]
گراف جهتدار: منظور از گراف جهت دار گرافی است که یالها در آن دارای جهت هستند. گراف جهت دار G زوج مرتب (V,E) است که V مجموعهای ناتهی و اعضای E زوجهای مرتب از اعضای V هستند. همانند گرافهای ساده، به اعضایV، راسهای G و به اعضای E، یالهای G میگوییم. همچنین به هر گراف جهتدار نموداری در صفحه نسبت میدهیم. به این صورت که به ازای هر راس G نقطهای در صفحه در نظر میگیریم و به ازای هر یال مانند (u,v) کمانی بین u و v رسم میکنیم و روی این کمان فلشی از u به v میگذاریم.
گراف مخلوط: گرافی است که در آن ممکن است برخی یالها جهت داشته باشند و برخی بدون جهت باشند. گراف مخلوط G، سهتایی مرتب G = (V, E, A) است که در آن V مجموعهی رئوس، E یالهای بدون جهت و A یالهای جهت دارمیباشند. گراف ساده و گراف جهتدار حالت خاصی از گراف جهت دار می باشند.
گراف وزندار: گراف وزندار، گرافی است که به هر یک از یالها یا به هریک از راسهای آن عددی نسبت داده شدهاست که وزن آن یال یا راس میباشد. وزن یال میتواند نشان دهنده هزینه، مسافت، زمان یا هر مشخصه دیگری از یال باشد. بعضی از نویسندهها به گراف وزندار گراف شبکهای میگویند.
قراردادها:
مرتبه و اندازۀ یک گراف: تعداد رأس های گراف G یعنی |V(G)| را مرتبهٔ آن گراف می گوییم و باp(G) نمایش می دهیم و تعداد یال های گراف یعنی |E(G)| را اندازهٔ گراف G می گوییم و با q(G) نمایش می دهیم. معمولاً برای راحتی کار به جای p(G) از p و به جای q(G) از q استفاده می کنیم.
درجۀ یک رأس: درجهٔ رأس v در گراف G برابر است با تعداد یال هایی از گراف G که به رأس v متصل اند و آن را با degG (v) یا به طور ساده تر با deg (v) یا d (v) نمایش می دهیم. اگر درجهٔ یک رأس فرد باشد آن را رأس فرد و اگر زوج باشد آن را رأس زوج می نامیم.
گراف K ـ منتظم: گرافی را که درجهٔ تمام رئوس آن با هم مساوی و برابر با عدد k باشند ،گراف k - منتظم می نامیم.
رأس تنها: به رأسی که درجهٔ آن صفر باشد؛ یعنی هیچ یالی به آن متصل نباشد، رأس تنها (یا ایزوله) می گوییم.[4]
گراف تهی: گرافی را که تمام رئوس آن رأس تنها باشند، یعنی هیچ یالی نداشته باشد ،گراف تهی می نامیم. بنابراین منظور از گراف تهیِ n رأسی، گرافی شامل n رأسِ تنها و بدون یال است.
دو رأس مجاور (همسایه): دو رأس u و v را دو رأسِ همسایه یا مجاور گوییم هرگاه توسط یالی به هم وصل شده باشند، یعنیuv ∈ E(G).
مجموعهٔ همسایه های یک رأس: فرض کنیم v ∈ V(G)، به مجموعهٔ رأس هایی از گراف G که به رأس v متصل هستند، "همسایگی باز رأسv " می گوییم و با NG(v) نمایش می دهیم. اضافه کردنِ خودِ رأسِ v به NG(v) "همسایگی بستهٔ رأسv " را به دست می دهد که آن را با NG[v] نمایش می دهیم. می توان این دو مجموعه را به صورت زیر نمایش داد: NG (v) = {u ∈ V (G )∶ uv ∈ E (G )} NG[v] =NG (v) ∪{v}
دو یال مجاور: دو یال را مجاور گوییم هرگاه رأسی وجود داشته باشد که هر دوی آنها به آن متصل باشند.
بزرگ ترین و کوچک ترین درجۀ یک گراف: بزرگ ترین عدد در بین درجات رئوس گراف G را با∆ ( G) و کوچک ترینِ آنها را با δ (G) نمایش می دهیم و به ترتیب آنها را ماکزیمم و مینیمم درجهٔ گراف می نامیم.
زیرگراف: یک زیرگراف از گراف G گرافی است که مجموعهٔ رئوس آن زیرمجموعه ای از مجموعهٔ رئوس گراف G، و مجموعهٔ یال های آن زیرمجموعه ای از مجموعهٔ یال های G باشد.
مکمل یک گراف: مکمل گرافی مانند G که آن را با G^c یا G ̅ نمایش می دهیم گرافی است که مجموعهٔ رئوس آن همان مجموعهٔ رئوس گراف G است و بین دو رأس از G^cیک یال است اگر و تنها اگر بین همان دو رأس درG یالی وجود نداشته باشد.
گراف کامل: گرافی را که هر رأس آن با تمام رئوسِ دیگرِ، مجاور باشد گراف کامل می نامیم. گراف کاملِ n رأسی را با Kn نمایش می دهیم. می توان گفت Kn یک گراف n رأسی وn-1 ــ منتظم است.
مسیر: اگر u و v دو رأس از گراف G باشند، یک مسیر از u به v (یک v ــ u مسیر) در G دنباله ای از رئوس دوبه دو متمایز در G است که از u شروع و به v ختم می شود به طوری که هر دو رأس متوالی این دنباله در G مجاور هم باشند. طول یک مسیر برابر است با تعداد یال های موجود در آن مسیر (یکی کمتر از تعداد رئوس موجود در آن مسیر). قرارداد می کنیم که دنبالهٔ متشکل از تنها یک رأسِv، یک مسیر است با طول صفر از رأس v به خودش. ( گرافی را که تنها از یک مسیرِ n رأسی تشکیل شده باشد با Pn نمایش می دهیم) .
دور: دنبالهٔ (n ≥ 3) v1 v2 v3 ... vn v1 از رئوس دو به دو متمایز که در آن هر رأس با رأس بعدی مجاور است را یک دور به طول n می نامیم. (گرافی را که تنها از یک دورِ n رأسی تشکیل شده باشد را با Cn نمایش می دهیم)
همبندی و ناهمبندی یک گراف: گراف G را همبند می نامیم هرگاه بین هر دو رأسِ آن حداقل یک مسیر وجود داشته باشد، در غیر این صورت آن را ناهمبند می نامیم.[5]
اندازه گراف
اندازه گراف تعداد یالهای یک گراف است و به صورت بیان میشود.
درجه رأسها
در نظریه گرافها، درجه یک راس به تعداد یالهای متصل به آن راس گفته میشود. به عبارت دیگر، درجه یک راس تعداد همسایگی (مجاورت)های مستقیم یک راس را بیان میکند. از آنجا که هر یال در گراف دو راس را به هم وصل میکند، مجموع درجه رأسهای یک گراف با دو برابر تعداد یالهای ان گراف برابر است.
گونههای گراف
گراف همبند گرافی است که بین همهٔ راسهای آن مسیری وجود داشته باشد.
درخت: گراف همبندى را که هیچ دوری نداشته باشد درخت مىنامیم نامیم. گرافهای K1 و K2 درخت اند و به ترتیب "تنها" درختهای با یک و دو راس هستند. ثابت میشود که در هر درخت بین هر دو راس دقیقا یک مسیر وجود دارد. در شکل زیر تمام درختهای از مرتبهی 1 تا 5 رسم شدهاند.
¬¬¬
کِیلی در سال 1857 میلادی درختها را در ارتباط با شمارش ایزومرهای مختلف هیدروکربنها کشف کرد. وقتی مثلا میگوییم دو ایزومر مختلف C4H10 وجود دارند منظورمان این است که دو درخت متفاوت با 14 راس وجود دارند که درجهی 4 راس از این 14 راس چهار و درجهی هریک از 10 راس باقیمانده یک است.[6]
گراف کامل

در نظریه گراف، یک گراف کامل، گرافیاست که بین هر دو راس آن دقیقاً یک یال وجود داشته باشد. یک گراف کامل از مرتبه n، دارای n راس و یال است که آن را با نشان میدهند. یک گراف کامل یک گراف منتظم از درجه n-۱ است.
گرافهای کاملی که p≥۳ قطعاً همیلتونی هستند.
گرافهای کاملی که p≥۳ و p فرد باشد (p=2k+۱) اویلری هستند، چون درجهٔ هر راس زوج است.
گراف پترسن
گراف پترسن گرافی با ۱۰ راس و ۳- منتظم است.
گراف دو بخشی(Bipartite Graph)
گرافی است که بتوان رئوس آن را به گونهای به دو مجموعهٔ u و v تقسیم کرد که گرافهای هر زیرگروه (v یا u)دو به دو با هم همسایه نبوده اما با حداقل یکی از رئوس مجموعهٔ دیگر همسایگی داشته باشند.
گراف دو بخشی کامل (Complete Bipartite Graph)
گراف دو بخشی کامل گرافی است که رئوس هر کدام از مجموعههای v یا u دو به دو با رئوس مجموعهٔ دیگر همسایه باشند. اگر حتی یکی از رئوس با همهٔ اعضای مجموعهٔ مقابل همسایه نباشد گراف دو بخشی کامل نیست.
مفهوم شهودی

فرض کنید در یک شرکت صنعتی تعدادی شغل بدون متصدی میباشند و تعدادی متقاضی برای این مشاغل اعلام آمادگی نمودهاند. حال این سؤال مطرح میشود که آیا میتوان به هر متقاضی شغلی متناسب او اختصاص داد؟ برای حل چنین مسئلهای که به مسئلهٔ تخصیص موسوم است، با استفاده از گراف میتوان وضعیتهای خاص را پیادهسازی نمود. بدین ترتیب که گروهی که متقاضی مشاغل هستند در مجموعهای به نام X و مجموعه مشاغل بدون متصدی را در مجموعهای به نام Y قرار میدهیم. گراف رسم شده چنین است که به بعضی از اعضای مجموعه X یک یا چند عضو از مجموعه Y توسط یالها وصل مینماید. به عبارت دیگر گراف به وجود آمده دارای یالهای xy است که هر متقاضی x را از مجموعه X به شغلهای مناسب y از مجموعه Y متصل مینماید. به عبارت دقیقتر هیچ دو راس متعلق به مجموعه X (متقاضیان) یا هیچ دو راس متعلق به مجموعه Y (مشاغل) توسط هیچ یالی به هم متصل نمیباشند. چنین گرافی را گراف دوبخشی یا دوپارچه میگویند.
تعریف
گراف دوبخشی گرافی است که بتوان مجموعه رئوس آن را به دو مجموعه X و Y چنان افراز نمود که هر یال آن دارای یک انتها در X و یک انتها در Y باشد، به گونهای که هیچ دوراسی در X یا در Y با هم مجاور نباشند. چنین افرازی را دوبخشی کردن گراف مینامند.
- یادآوری: منظور از افراز یک مجموعه چون A به چند مجموعه، تقسیم مجموعه A به چند مجموعه ناتهی دیگر است که باهم اشتراکی نداشته باشند و اجتماع همه آنها برابر مجموعه A باشد؛ و در اینجا اگر V به عنوان مجموعه رئوس باشد افراز V به دو مجموعه X و Y (ناتهی) به این صورت است که: XY = V و XY =
- مثال
به عنوان مثال گراف زیر یک گراف دو بخشی است:
گراف ساده
گراف ساده: هر گراف G زوج مرتبی مانند (V,E) است که در آن V مجموعهای متناهی و ناتهی است و E زیرمجموعهای از تمام زیرمجموعههای دو عضوی V میباشد. اعضای V را رأسهای G و اعضای E را یالهای G مینامیم. به بیان سادهتر بین دو رأس یک گراف ساده حداکثر یک یال وجود دارد و هیچ طوقهای (یعنی یالی که رأس را به خودش وصل میکند) نیز وجود نداشته باشد.[7]
گراف همیلتونی
گراف سادهٔ G از مرتبه V هرگاه دوری به طول V در آن یافت شود.
گراف چرخ
هر گراف G که دارای n راس باشد کهn≥۴ و یکی از رئوس از درجهٔ n-۱ و بقیه از درجهٔ سه باشند، را یک گراف چرخ مینامیم- مانند مثالهای زیر:
گراف چرخn راسی را با nW نمایش میدهیم.
گراف چندگانه
گراف چندگانه: هرگاه بین دو رأس متمایز از یک گراف بیش از یک یال وجود داشته باشد، آن را یک گراف چند گانه میگوییم.
گراف مکعبی
یک گراف «k مکعب» (k-Cube) گرافی است که رئوس آنk تایی از «صفر» و «یک» هستند که دو رأس آن به یکدیگر متصل هستند اگر و فقط اگر دو رأسشان دقیقاً در یک مؤلفه با یکدیگر تفاوت داشته باشند. بهعبارت دیگر اگر kعددی طبیعی باشد منظور از «kمکعب» گرافی است که رأسهای آن همهٔ دنبالههای رقمی از «صفر» و «یک» هستند و دو رأس در این گراف مجاور بوده هرگاه دنبالههای متناظرشان دقیقاً در یک مؤلفه اختلاف داشته باشند (شکل ۱).
میتوان نشان داد که یک گراف «k مکعب» (k-Cube) دارای ویژگیهایی نظیر ذیل است:
- تعداد رؤوس =۲k
- تعداد یالها=k*۲(k-1)
- گرافی «دوبخشی» (Bipartite) است.
گراف جهت دار
گراف جهت دار: هر گراف G زوج مرتبی مانند (V,E) است که در آن V مجموعهای متناهی و ناتهی است و E زیرمجموعهای از مجموعهٔ تمام زوج مرتبهای متشکل از اعضای V است.
گراف جهتدار و کاربردهای آن
گراف جهت دارو کاربردهای آنگراف جهت دار D، یک سه تایی مرتب(O(D) و A(D) و (V(D)است که تشکیل شده از یک مجموعه ناتهی V(D) از راسها ویک مجموعه (D) A مجزای از V(D)از کمانها و یک تابع وقوع O(D)که به هر کمان D یک زوج مرتب از راسهای D- که الزاماً متمایز نیستند- را نسبت میدهد. اگر a یک کمان وu,v دو راس باشند بهطوری که(u,v) =(a)O (D)، آنگاه میگوییم که u,a را به v وصل کردهاست؛ u، دم v,a سرa نامیده میشود.
گراف مسطح
گراف مسطح: گراف مسطح گرافی است که میتوان آن را در یک صفحه محاط کرد به گونهای که یالهایش یکدیگر را تنها در رأسها قطع کنند. به این گراف هامنی نیز گفته میشود.
در بین گرافهای کامل فقط گرافهایی با تعداد راس مساوی یا کمتر از 5 (p≤۵) را، میتوان به صورت مسطح رسم کرد.
گراف وزندار
گراف وزندار: در یک گراف وزن دار، به هر یال یک وزن (عدد) نسبت داده میشود. معمولاً اعداد حقیقی به عنوان وزن یالها استفاده میشوند. اما بسیاری از الگوریتمهای پر کاربرد فقط برای گرافهایی که دارای وزن صحیح یا مثبت هستند طراحی شدهاند.
گرافهای تماس تلفنی
میتوان از گرافهای تماس تلفنی رأی مدل کردن تماسهای تلفنی برقرار شده در یک شبکه مانند شبکه تلفن راه دور استفاده کرد؛ که در ان رأسها شماره تلفنها و یالها ارتباطهای برقرار شده بین شماره تلفنها است.
گراف همپوشانی منابع غذایی در بومشناسی
گراف همپوشانی منابع غذایی در بوم شناسی یکی از کاربردهای گراف در رشتههای دیگر مانند زیستشناسی است، در این گراف منابع غذایی یک اکوسیستم مدل میشوند و آگاهی مناسبی از رقابتهای میان هر گونه ارائه میدهند
گرافهای روابط آشنایی
گراف روابط آشنایی: از این مدل گراف میتوانیم برای نمایش روابط متعدد بین افراد استفاده کنیم.
برای مثال، میتوانیم از یک گراف ساده برای نمایش این که آیا دو نفر همدیگر را میشناسند، یعنی آیا آشنا هستند، استفاده کنیم.
گرافهای همکاری
گرافهای همکاری برا مدل کردن همکاری نویسندگان در نوشتن مقالات علمی، میتوان از یک گراف همکاری استفاده کرد. در یک گراف همکاری، رئوس، افراد (شاید محدود به اعضای یک انجمن دانشگاهی خاص) را نمایش میدهند و یالها در صورتی دو نفر را بهم وصل میکند که آن دو نفر، مقالهای را بهطور مشترک نوشته باشند.
گراف نقشه راهها
گراف نقشه راهها از گرافها میتوان برای مدل کردن نقشه راهها استفاده کرد. در این گونه مدلها، رئوس، نمایش دهنده تقاطعها و یالها، نمایش دهنده جادهها هستند. یالهای بدون جهت، جادههای دو طرفه و یالهای جهت دار، جادههای یک طرفه را نشان میدهند.
گراف تقدم و پردازش همزمان
با اجرای همزمان جملات مشخص یک برنامه کامپیوتری، میتوان آن برنامه را سریع تر اجرا کرد. مهم است که جملهای که نتایج جملاتی که هنوز اجرا نشدهاند، نیاز دارد، اجرا نشود. وابستگی جملات به جملات پیشین را میتوان با یک گراف (ریاضی) جهت دار نمایش داد. هر جمله با یک راس نمایش داده میشود و در صورتی یالی بین یک راس و راس دوم در نظر گرفته میشود که جمله نشان داده میشود با راس دوم نتواند قبل از اجرای جمله نشان داده شدهاست با راس اول اجرا شود. این گراف (ریاضی) یک گراف (ریاضی) تقدم نامیده میشود.[8]
مثال
در شکل زیر یک برنامه کامپیوتری و گراف (ریاضی) ان نشان داده شدهاست. برای مثال این گراف نشان میدهد که جمله S_5 نمیتواند قبل از جملات S_2 , S_3 و S_1 اجرا شود.
ویژگیهای گرافهای ویژه
- اگر درجهٔ همهٔ رأسها در گراف ساده با هم برابر و برابر بزرگترین درجهٔ ممکن (یعنی p-۱) باشد، گراف مورد نظر منتظم کامل است. در این گونه گرافها، رابطهٔ میان رأسها و یالها چنین است:
- که در آن تعداد راسها، و تعداد یالها است.
- اگر گراف همبند باشد (یعنی از هر نقطه بتوان به یک نقطه دلخواه دیگر رسید) ولی دور نداشته باشد (یعنی هیچ نقطهای از دوراه به نقطهٔ بعدی نرسد) میگویند گراف درختی است. در اینگونه گرافها فرمول زیر صدق میکند (شرط لازم):
- که در آن تعداد رأسها، و تعداد یالها است.[9]
- گراف اویلری و همیلتونی:گاهی اوقات ما میخواهیم در یک گراف حرکت کنیم. به اینصورت که از راسی به راسی دیگر برویم. در اینصورت ممکن است برای ما مهم باشد که از روی یال یا راس تکراری حرکت نکنیم (مشابه مسئلهٔ فروشندهٔ دوره گرد). این مسئله در صرفه جویی زمان و هزینه هم مهم است. (یعنی مبحث بهینهسازی). دراینجا دو موضوع گرافهای اویلری (دور زدن در گراف بدون یال تکراری) و همیلتونی (دور زدن بدون راس تکراری) مطرح میشود. به راحتی میتوان بررسی کرد که راسهای گراف اویلری باید درجهٔ زوج داشته باشند. اما اینکه شرایط کامل لازم و کافی برای همیلتونی بودن یک گراف چیست هنوز حل نشده ماندهاست.
گرافهای کاربردی
کاربردها
از گرافها برای حل مسایل زیادی در ریاضیات و علوم کامپیوتر استفاده میشود. ساختارهای زیادی را میتوان به کمک گرافها به نمایش درآورد. برای مثال برای نمایش چگونگی رابطه وب سایتها به یکدیگر میتوان از گراف جهت دار استفاده کرد. به این صورت که هر وب سایت را به یک راس در گراف تبدیل میکنیم و در صورتیکه در این وب سایت لینکی به وب سایت دیگری بود، یک یال جهت دار از این راس به راسی که وب سایت دیگر را نمایش میدهد وصل میکنیم.
از گرافها همچنین در شبکهها، طراحی مدارهای الکتریکی، اصلاح هندسی خیابانها برای حل مشکل ترافیک، و… استفاده میشود. مهمترین کاربرد گراف مدلسازی پدیدههای گوناگون و بررسی بر روی آنهاست. با گراف میتوان به راحتی یک نقشه بسیار بزرگ یا شبکهای عظیم را در درون یک ماتریس به نام ماتریس وقوع گراف ذخیره کرد یا الگوریتمهای مناسب مانند الگوریتم دایسترا یا الگوریتم کروسکال و… را بر روی آن اعمال نمود. در این جا به بررسی گرافهایی میپردازد که میتوان آنها را به نحوی روی صفحه کشید که یالها جز در محل رأسها یکدیگر را قطع نکنند. این نوع گراف در ساخت جادهها و حل مسئله کلاسیک و قدیمی سه خانه و سه چاه آب به کار میرود.
کاربرد گراف بازهها از گرافها برای حل مسایل زیادی در ریاضیات و علوم کامپیوتر استفاده میشود. ساختارهای زیادی را میتوان به کمک گرافها به نمایش درآورد.
درخت و ماتریس درخت در رشتههای مختلفی مانند شیمی مهندسی برق و علم محاسبه کاربرد دارد. کیرشهف در سال ۱۸۴۷ میلادی هنگام حل دستگاههای معادلات خطی مربوط به شبکههای الکتریکی درختها را کشف و نظریه درختها را بارور کرد. کیلی در سال ۱۸۵۷ میلادی درختها را در ارتباط با شمارش ایزومرهای مختلف هیدروکربنها کشف کرد وقتی مثلاً میگوییم در ایزومر مختلف c4h۱۰ وجود دارد منظورمان این است که دو درخت متفاوت با ۱۴ راس وجود دارند که درجه ۴ راس از این ۱۴ راس جهار و درجه هر یک از ۱۰ راس باقیمانده یک است. اگر هزینه کشیدن مثلاً راهآهن بین هر دو شهر ازp شهر مفروض مشخص باشد ارزانترین شبکهای که این p شهر را به هم وصل میکند با مفهوم یک درخت از مرتبه p ارتباط نزدیک دارد. به جای مسئله مربوط به راهآهن میتوان وضعیت مربوط به شبکههای برقرسانی و لولهکشی نفت و لولهکشی گاز و ایجاد کانالهای آبرسانی را در نظر گرفت. برای تعیین یک شبکه با نازلترین هزینه از قاعدهای به نام الگوریتم صرفه جویی استفاده میشود که کاربردهای فراوان دارد. از گرافها میتوان به عنوان کدهای کمکی نام برد که به DVB Playerها در بالا بردن قابلیتهای آنها کمک میکنند. گرافها دارایی مزایای مختلفی هستند که شفاف تر کردن و واضحتر کردن تصویر و کاهش مصرف CPU به عنوان یکی از اصلیترین مزایای آنها بهشمار میرود.
پانویس
- بابلیان، «مباحثی از نظریه گراف»، مباحثی در ریاضیات گسسته، ۱۵۱.
- بهزاد و دیگران، «گرافها و کاربردهای آن»، ریاضیات گسسته، ۲.
- بابلیان، «مباحثی از نظریه گراف»، مباحثی در ریاضیات گسسته، ۱۵۱.
- کتاب آشنایی با نظریهٔ گراف نوشتهٔ علیرضا علیپور، انتشارات فاطمی.
- حمیدرضا امیری، ابراهیم ریحانی, محمدرضا سید صالحی و امید نقشینه ارجمند (۱۳98). ریاضیات گسسته. تهران: شرکت چاپ و نشر کتابهای درسی ایران. 9 شابك 2 3111 05 964 78.
- هزاد، مهدی؛ رجالی، علی؛ عمیدی، علی؛ محمودیان، عبادالله (۱۳۸۵). ریاضیات گسسته. تهران: شرکت چاپ و نشر کتابهای درسی ایران. شابک ۹۶۴-۰۵-۰۱۰۳-۴.
- احمدی فولادی، یاسر؛ محمودیان (۱۳۹۰). سید عبادالله، ویراستار. آشنایی با گراف. فاطمی. پارامتر
|تاریخ بازیابی=نیاز به وارد کردن|پیوند=دارد (کمک) - Kenneth H, Rosen (1998). "Graph". Discrete Mathematics and its Applications. SIGS Reference Library. William C Brown Pub; 4th edition. ISBN 0072899050. Retrieved 2007. Check date values in:
|بازبینی=(help) - کتاب ریاضیات گسسته پیش دانشگاهی رشته ریاضی فصل اول
منابع
- بابلیان، اسماعیل (۱۳۸۶). مباحثی در ریاضیات گسسته. تهران: مبتکران. شابک ۹۷۸-۹۶۴-۵۹۹۳-۳۲-۸.
- بهزاد، مهدی؛ رجالی، علی؛ عمیدی، علی؛ محمودیان، عبادالله (۱۳۸۵). ریاضیات گسسته. تهران: شرکت چاپ و نشر کتابهای درسی ایران. شابک ۹۶۴-۰۵-۰۱۰۳-۴.
- کتاب آشنایی با نظریهٔ گراف نوشتهٔ علیرضا علیپور، انتشارات فاطمی
- گریمالدی، رالف پ. (۱۳۷۹). ریاضیات گسسته و ترکیبیاتی. ۳. ترجمهٔ دکتر محمدعلی رضوانی و دکتر بیژن شمس. تهران: انتشارات فاطمی. شابک ۹۶۴-۳۱۸-۲۵۶-۸.
- وست، داگلاس بی. (۱۳۸۶). آشنایی با نظریهٔ گراف. ترجمهٔ دکتر بیژن شمس. تهران: گسترش علوم پایه. شابک ۹۶۴-۷۸۱۷-۲۶-۶.
- کتاب نظریه گرافها و کاربردهای آن نوشته باندی و مورتی، ترجمه حمید ضرابی زاده، مؤسسه دیباگران تهران
- کتاب ریاضیات گسسته نوشته ر. پ. گریمالدی، مرکز نشر دانشگاهی
- کتاب نظریهٔ الگوریتمی و کاربردی گرافها نوشته گری چارتراند، آرترود اولرمن، ترجمه دکتر سید مهدی تشکری هاشمی، انتشارات دانشگاه امیرکبیر
- Graph Theory Software نرمافزارهای گراف تولید شده در دانشگاه صنعتی شریف
- . دنیای ریاضیات http://mathworld.wolfram.com/Graph.html. Retrieved 6 March 2014. Missing or empty
|title=(help)
Kenneth H, Rosen (1998). "Number Theory and Cryptography". Discrete Mathematics and its Applications. SIGS Reference Library. William C Brown Pub; 4th edition. ISBN 0072899050. Retrieved 2007. Check date values in: |بازبینی= (help)
