فرایند وینر
فرایند وینر، یک فرایند تصادفی پیوسته در زمان در ریاضیات است که به افتخار نوربرت وینر نامگذاری شدهاست. این فرایند به اسم حرکت براونی استاندارد هم شناخته میشود، به خاطر کارهای رابرت براون. این یکی از بهترین فرایند هایLévy است. (فرایند تصادفی Càdlàg با خاصیت رشد مستقل مانا) و در ریاضیات محض و کاربردی، اقتصاد، مالیه ریاضی و فیزیک کاربردهای زیادی دارد.
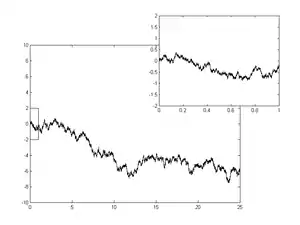
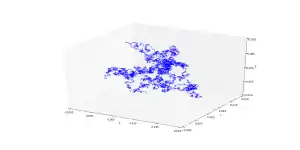
فرایند وینر هم در ریاضیات محض و هم در ریاضبات کاربردی کاربرد دارد. کاربرد آن در ریاضیات محض برای بررسی زمان-پیوسته مدل مارتینگل (martingales) است که یک مدل برای بررسی این است که چقدر یک فرایند تصادفی میتواند پیچیده باشد است. در نتیجه نقش حیاتی درمحاسبات احتمالی و انتشار فرایندها و حتی نظریه پتانسیل دارد. این فرایند از Schramm–Loewner تکامل نتیجه میشود. در ریاضیات کاربردی، فرایند وینر برای نشان دادن تجمیع نویز سفید فرایند گوسی استفاده میشود بنابراین در مهندسی الکترونیک برای مدل کردن نویز از آن استفاده میشود (نویز Brownian را هم ببینید.) همچنین به عنوان ابزار خطا در تئوری فیلتر و نیروهای ناشناخته در تئوری کنترل کاربرد دارد.
فرایند وینردر سراسر علوم محاسباتی کاربردهای متنوعی دارد. در فیزیک از آن برای مطالعه حرکت براونی استفاده میشود همچنین در مطالعه دربارهٔ انتشار ذرات معلق در مایع و انواع دیگر انتشار به صورت فوکر–پلانک و معادلات انگوین کاربرد دارد. همچنین پایههای دقیقی برای توصیف فرمولبندی مسیر انتگرال در مکانیک کوانتومی به ما میدهد (با فرایند وینر و به وسیله فرمول فاینمن -کاک میتوان یک راه حل برای معادله شرودینگر ارائه داد.) و برای مطالعه تورم ابدی در کیهانشناسی فیزیکی نیز کاربرد دارد. این فرایند نقش برجستهای در تئوری ریاضی امور مالی به ویژه Black–Scholes به عنوان مدلی برای قیمت گذاری دارد.
مشخصات فرایند وینر
فرایند وینر Wt با مشخصه زیر تعیین میشود:[1]
- به صورت قریب به یقین W0 = ۰
- W رشد مستقل داشته باشد: یعنی Wt+u - Wt مستقل از(σ(Ws: s ≤ t برای u ≥ ۰
- W رشد گوسی داشته باشد: یعنی Wt+u - Wt توزیع نرمال با میانگین ۰ و واریانس u باشد.Wt+u−Wt ~ N(0, u)
- W مسیر پبوسته باشد: یعنی با احتمال ۱تابع Wt در t پیوسته باشد.
رشد مستقل داشته باشد به این معنی است که اگر ۰ ≤ s1 <t1 ≤ s2 <t2 آنگاه Wt1−Ws1 و Wt2−Ws2 متغیر تصادفی مستقل باشند.
فرایند وینر همچنین میتواند به مشخصهای تعیین شود به نام مشخصه Lévy که میگوید که فرایند وینر به صورت قریب به یقین پیوسته martingale با W0 = ۰ باشد و درجه دوم تنوع معادل wt,wt] = t] داشته باشد (که به این معنی است که Wt2−t نیز martingale باشد.).
سومین مشخصه این است که فرایند وینر یک طیفی نمایندگی به صورت سری سینوسی با ضرایب مستقل به صورت متغیر تصادفی N(0, 1) باشد. این نمایش میتواند با استفاده از قضیه Karhunen–Loève بدست آید.
دیگر ویژگی فرایند وینر داشتن انتگرال معین (از صفر تا زمان t) با میانگین ۰ است و واریانس ۱ و همبستگی تابع ضربه به صورت فرایند گوسی سفید است.
فرایند وینر را میتوان به عنوان حد پوسته پوسته شدن یک تصادفی پیادهروی یا هر فرایند تصادفی زمان-گسسته با خاصیت رشد مستقل مانا در نظر گرفت. این به عنوان قضیه Donsker شناخته میشود. مثل پیادهروی تصادفی، فرایند وینر هم در یک یا دو بعد تکرار شونده است (یعنی به صورت قریب به یقین برای هر مبدأ به یکی از همسایهها میرسد) ولی در سه بعد و بالاتر تکرار شونده نیست. بر خلاف پیادهروی تصادفی مستقل از مقیاس نیست. یعنی
برای هر ثابت غیر صفر a یک فرایند وینر است. مقیاس وینر یک قاتوت احتمال در فضای توابع پیوسته g با g(0)=۰ بر اساس فرایند وینر است. انتگرال بر اساس مقیاس وینر انتگرال وینر نام دارد.
فرایند وینر به عنوان یک حد از گام تصادفی
فرض کنید متغیر تصادفی مستقل با توزیع یکسان با میانگین ۰ و واریانس ۱ باشد. برای هر n یک فرایند تصادفی زمان پیوسته در نظر بگیرید:
این یک تابع گام تصادفی است. چون که ها مستقل هستند، اختلاف ها مستقل از هم میشوند. با توجه به قضیه حد مرکزی برای nهای بزرگ به توزیع نزدیک میشود. این اتفاق باعث میشود که احتمال بدهیم با افزایش n , تبدیل به فرایند وینر خواهد شد، و این احتمال درست است! اثبات این قضیه با تئوری Donsker بدست میآید.
خواص فرایند وینر یک بعدی
خواص اساسی
چگالی احتمال تابع بدون شرط، با توزیع نرمال با میانگین ۰ و واریانس t در زمان ثابت t:
- https://wikimedia.org/api/rest_v1/media/math/render/svg/c1a3c0bbe12d2a1d5cafdc35e1c836537e6cff27
- در این فرایند میانگین ۰ است:
و واریانس آن، با توجه به فرمول اصلی محاسبه واریانس t است :
کوواریانس و همبستگی
کوواریانس و همبستگی فرایند:
میانگین و واریانس به سادگی و با استفاده از تعریف توزیع نرمال بدست میآید. در نتیجه
کوواریانس و همبستگی فرایند از تعریف و اینکه رشد در بازههای غیر مشترک مستقل هست بدست میآید، که ما تنها از ناهمبسته بودن آنها استفاده میکنیم. فرض کنید که t1 <t2.
اگر \W_{t2} به صورت زیر جایگزین شود:
به عبارت زیر میرسیم:
از آنجا که W(t1) = W(t1) − W(t0) و W(t2) − W(t1) مستقل هستند
در نتیجه
نمایش وینر
وینر (۱۹۲۳) همچنین یک نمایش از مسیر براونی، در شرایط تصادفی سریهای فوریه داد. اگر ها متغیرهای گوسی مستقل با میانگین صفر و واریانس ۱ باشند، آنگاه:
و
نشان دهنده حرکت براونی در فاصله
یک حرکت براونی در فاصله (ر.ک. Karhunen–Loève قضیه).
حداکثر نمونه
توزیع مشترک حداکثر نمونه
که در آن Wt:
برای پیدا کردن توزیع بدن شرط −∞ <w ≤ m:
و میانگین آن[2]
برخی از خواص مسیرهای نمونه
مشخصات فرایند وینر
برای هر c> 0 فرایند یک فرایند وینر دیگر است.
فرایند وینر حد پیادهروی تصادفی
فرایند در بازه۰ ≤ t ≤ ۱ همانند فرایند Wt در بازه ۰ ≤ t ≤ ۱ است.
وارونگی زمانی
فرایند یک فایند وینر دیگر است.
یک کلاس از Brownian martingales
اگر چند جملهای p(x, t) شرایط PDE را ارضا کند
آنگاه فرایند تصادفی
یک مارتینگیل است.
مثال: یک مارتینگیل است که نشان میدهد که متغیر درجه دو W در بازه [0, t] برابر t است. این نتیجه میدهد که میانگین زمان اولین خروج W در بازه (−cبا c) برابر با c2 است.
بهطور کلی برای هر چند جملهای p(x, t) فرایند تصادفی زیر یک مارتینگیل است
که در آن a چند جملهای زیر است:
مثال: و فرایند
یک مارتینگیل است که نشان میدهد که متغیر درجه دو مارتینگیل [0, t] برابر است با
دربارهٔ توابع p(xa, t) در حالت کلی (غیر از چندجملهای) مارتینگیل محلی (local martingales) را ببینید.
مجموعهای از تمام توابع w با این خواص کامل مقیاس وینر است. یک مسیر (تابع نمونه) از فرایند وینر، قریب به یقین تمام این خواص را دارد.
خواص کیفی
- برای هر ε> ۰ تابع w هم مقادیر مثیت و هم مقادیر منفی را در بازه (۰, ε) دارد.
- تابع w در همه جا پیوستهاست اما در هیچ جا مشتق پذیر نیست (مانند تابع وایرشتراس).
- حداکثرهای محلی تابع w متراکم و شمارا هستند. نقاط حداکثر دوبه دومتفاوت هستند. هر حداکثر محلی به صورت زیر تیز است: اگر w در tحداکثر محلی داشته باشد آنگاه
- برای حداقلهای محلی هم بهطور مشابه است.
- تابع w هیچ نقطه افزایش محلی ندارد. یعنی هیچ t> 0 وجود ندارد که برای یک ε در بازه (0, t) شروط زیر را ارضا کند. اولاً: w(s) ≤ w(t) برای هر sدر بازه (t − ε , t) و ثانیاً w(s) ≥ w(t) برای هر s در بازه (t, t + ε). (افزایش محلی از اینکه w در بازه (t − ε , t + ε) افزایش یابد، شرط ضعیفتری است) برای کاهش محلی هم بهطور مشابه است.
- تابع w در هر بازه زمانیتغییرات بدون محدودیت دارد.
- متغیر درجه دوم wدر بازه [0,t] برابر t است.
در مقایسه با ارزش واقعی مورد پیچیده به ارزش شرط است بهطور کلی یک زمان-تغییر پیچیده-ارزش وینر روند. برای مثال شرط 2Xt + iYt است (در اینجا Xtبا Yt مستقل هستند وینر فرایندهای مانند قبل).
منابع
- Durrett 1996, Sect. 7.1
- Shreve, Steven E (2008). Stochastic Calculus for Finance II: Continuous Time Models. Springer. pp. 114. ISBN 978-0-387-40101-0.
