قضیه دیورژانس
قضیه دیورژانس (به انگلیسی: Divergence theorem)، که با نام قضیه گاوس و قضیه اوستروگرادسکی هم شناخته میشود، قضیهای در حساب برداری است که شار یک میدان برداری گذرنده از یک سطح را به رفتار آن میدان برداری در داخل آن سطح مربوط میکند.
| بخشی از سری مقالات |
| حسابان |
|---|
|
این قضیه بیان میکند که شار یک میدان برداری گذرنده از یک سطح بسته، با انتگرال حجمی دیورژانس آن میدان در داخل آن سطح بسته برابر است. قضیه دیورژانس، یک قضیه مهم در ریاضیات مهندسی و بهویژه در الکترواستاتیک، پدیده های انتقال و دینامیک شارهها است.
در فیزیک و مهندسی، معمولاً قضیه دیورژانس در فضای سهبعدی مورد استفاده قرار میگیرد، ولی این قضیه به فضای nبعدی (n عدد طبیعی دلخواه) تعمیم پیدا میکند. در حالت یکبعدی، این قضیه معادل با قضیه اساسی حسابان است. همچنین، این قضیه، یک حالت خاص از قضیه عمومیتر استوکس است.[1]
بیان ریاضیاتی
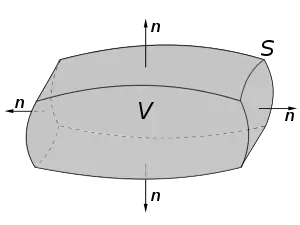
اگر V یک زیرمجموعه از Rn باشد (در حالت n=3، محدوده V یک حجم در فضای سهبعدی خواهد بود) که یک مجموعه فشرده بوده و یک مرز هموار S دارد و F یک میدان برداری مشتقپذیر در همسایگی V باشد، سپس قضیه دیورژانس را میتوان به صورت زیر بیان کرد:
سمت چپ معادلهٔ بالا، انتگرال حجمی در داخل V و سمت راست آن، انتگرال سطحی بر روی مرز آن (S) است.
پانویس
- Stewart, James (2008), "Vector Calculus", Calculus: Early Transcendentals (6 ed.), Thomson Brooks/Cole, ISBN 978-0-495-01166-8
