انتگرال‌گیری کانتور

یک نتیجهٔ اولیه در آنالیز مختلط این است که انتگرال z⁻¹ روی مسیر C که دایرهٔ واحد (یا هر منحنی جردان دور) باشد، ۲πi است. اجازه دهید انتگرال زیر را محاسبه کنیم

${\displaystyle \oint _{C}{1 \over z}\,dz.}$

برای محاسبهٔ این انتگرال از دایرهٔ واحد z|=۱| به عنوان مسیر استفاده می‌کنیم، که می‌توان آن را به شکل γ(t) = e^it با t ∈ [۰, ۲π] پارامتری کرد. توجه داشته باشید که γ'(t) = ie^it. اکنون با جایگزینی z به جای این داریم:

${\displaystyle \oint _{C}{1 \over z}\,dz=\int _{0}^{2\pi }{1 \over e^{it}}ie^{it}\,dt=i\int _{0}^{2\pi }e^{-it}e^{it}\,dt=i\int _{0}^{2\pi }1\,dt}$

${\displaystyle =\left.t\right]_{0}^{2\pi }i=(2\pi -0)i=2\pi i}$

که مقدار انتگرال است.

انتگرال زیر را در نظر بگیرید

${\displaystyle \int _{-\infty }^{\infty }{1 \over (x^{2}+1)^{2}}\,dx.}$

برای محاسبهٔ این انتگرال، به تابع مختلط زیر توجه می‌کنیم

${\displaystyle f(z)={1 \over (z^{2}+1)^{2}}}$

که روی i و −i نقطهٔ تکین دارد. با این حال، ما می‌خواهیم یک مسیر انتخاب کنیم که انتگرال حقیقی مقدار را احاطه کند، بنا بر این یک نیم دایره مانند شکل بالا انتخاب می‌کنیم، و آن را گسترش می‌دهیم تا تمام محور حقیقی را در بر بگیرد (a به سمت بی‌نهایت میل می‌کند). این مسیر را C می‌نامیم.

مشاهده کنید که

${\displaystyle f(z)={1 \over (z^{2}+1)^{2}}={1 \over (z+i)^{2}(z-i)^{2}}.}$

از آنجایی که تنها نقطهٔ تکین در مسیر روی i است، می‌توانیم بنویسیم

${\displaystyle f(z)={{1 \over (z+i)^{2}} \over (z-i)^{2}},}$

که تابع را به فرمی درمی‌آورد که می‌توان مستقیماً از فرمول استفاده کرد. آنگاه طبق فرمول،

${\displaystyle \oint _{C}f(z)\,dz=\oint _{C}{1 \over (z^{2}+1)^{2}}\,dz=\oint _{C}{{1 \over (z+i)^{2}} \over (z-i)^{2}}\,dz=2\pi i{\frac {d}{dz}}\left(\left.{1 \over (z+i)^{2}}\right)\right|_{z=i}}$

${\displaystyle =2\pi i\left.\left({-2 \over (z+i)^{3}}\right)\right|_{z=i}=2\pi i(-i/4)={\pi \over 2}}$

اگر کمان نیم دایره راA بنامیم، باید نشان دهیم وقتی a به سمت بی‌نهایت میل می‌کند، انتگرال روی A به سمت صفر میل می‌کند – با استفاده از لم تخمین (estimation lemma)

${\displaystyle \left|\oint _{A}f(z)\,dz\right|\leq ML}$

که M یک حد بالا برای |f(z)| و L طول A است. اکنون

${\displaystyle \int _{A}f(z)\,dz\leq {a\pi \over (a^{2}+1)^{2}}\rightarrow 0\ \mathrm {as} \ a\rightarrow \infty }$

بنابر این

${\displaystyle \int _{-\infty }^{\infty }f(z)\,dz={\pi \over 2}.\quad \square }$

سری Laurent را برای f(z) روی i، تنها نقطهٔ تکینی که باید به آن توجه کنیم، در نظر بگیرید. داریم

${\displaystyle f(z)={1 \over 4(z-i)^{2}}+{-i \over 4(z-i)}+{3 \over 16}+{i \over 8}(z-i)+{-5 \over 64}(z-i)^{2}+\cdots }$

با بازبینی روش متوجه می‌شویم که مانده،i/4 است، بنا بر این طبق قضیهٔ reisdue داریم

${\displaystyle \oint _{C}f(z)\,dz=\oint _{C}{1 \over (z^{2}+1)^{2}}\,dz=2\pi i\mathrm {Res} _{z=i}f=2\pi i(-i/4)={\pi \over 2}\quad \square }$

اگر کمان نیم دایره را A بنامیم، باید نشان دهیم وقتی a به سمت بی‌نهایت میل می‌کند، انتگرال روی A به سمت صفر میل می‌کند – با استفاده از لم تخمین (estimation lemma)

${\displaystyle \left|\oint _{A}f(z)\,dz\right|\leq ML}$

که M یک حد بالا برای |f(z)| و L طول A است. اکنون

${\displaystyle \int _{A}f(z)\,dz\leq {a\pi \over (a^{2}+1)^{2}}\rightarrow 0\ \mathrm {as} \ a\rightarrow \infty }$

بنابر این

${\displaystyle \int _{-\infty }^{\infty }f(z)\,dz={\pi \over 2}.\quad \square }$

که همان نتیجه‌ای است که در بالا به آن رسیدیم.

ممکن است سؤالی پیش بیاید مبنی بر این که آیا نباید نیم دایره را طوری در نظر بگیریم که نقطهٔ تکین دیگر، −i را در بر بگیرد؟ برای انتگرال‌گیری روی محور حقیقی در جهت صحیح، مسیر باید در جهت عقربه‌های ساعت (منفی) حرکت کند، که علامت انتگرال را عوض می‌کند. این کار استفاده از روش مانده را تحت تأثیر قرار نمی‌دهد.

انتگرال

${\displaystyle \int _{-\infty }^{\infty }{e^{itx} \over x^{2}+1}\,dx}$

با تکنیک‌های حسابان پایه‌ای قابل محاسبه نیست. ما آن را به صورت حدی از انتگرال‌های مسیر که روی خط حقیقی از −a تاa و سپس در خلاف عقربه‌های ساعت روی یک نیم دایره به مرکز ۰ از a تا −a حرکت می‌کند، محاسبه می‌کنیم. انتگرال مسیر به صورت زیر است:

${\displaystyle \int _{C}{e^{itz} \over z^{2}+1}\,dz.}$

از آنجایی که تابع e^itz یک تابع پیوسته است، نقطهٔ تکین در تابع بالا فقط زمانی پیش می‌آید که مخرج z² + 1 صفر باشد. از آنجایی که z² + 1 = (z + i)(z − i) این اتفاق فقط زمانی می‌افتد که z = i یا z = −i. تنها یکی از این نقاط در منطقه‌ای هستند که توسط این مسیر احاطه شده‌است. مانده برای f(z) در z = I برابر است با

${\displaystyle \lim _{z\to i}(z-i)f(z)=\lim _{z\to i}(z-i){e^{itz} \over z^{2}+1}=\lim _{z\to i}(z-i){e^{itz} \over (z-i)(z+i)}}$

${\displaystyle =\lim _{z\to i}{e^{itz} \over z+i}={e^{iti} \over i+i}={e^{-t} \over 2i}.}$

بنا بر قضیهٔ مانده داریم

${\displaystyle \int _{C}f(z)\,dz=2\pi i\cdot \operatorname {Res} _{z=i}f(z)=2\pi i{e^{-t} \over 2i}=\pi e^{-t}.}$

C را می‌توان به دو قسمت پاره خط و کمان تقسیم کرد طوری که

${\displaystyle \int _{\mbox{straight}}+\int _{\mbox{arc}}=\pi e^{-t},}$

و بنا بر این

${\displaystyle \int _{-a}^{a}=\pi e^{-t}-\int _{\mbox{arc}}.}$

می‌توان نشان داد که اگر t>0 آنگاه

${\displaystyle \int _{\mbox{arc}}{e^{itz} \over z^{2}+1}\,dz\rightarrow 0\ {\mbox{as}}\ a\rightarrow \infty .}$

بنا بر این اگر t>0 آنگاه

${\displaystyle \int _{-\infty }^{\infty }{e^{itz} \over z^{2}+1}\,dz=\pi e^{-t}.}$

بحثی مشابه با کمانی که دور −i (به جای i) می‌گردد نشان می‌دهد که اگر t<0 آنگاه

${\displaystyle \int _{-\infty }^{\infty }{e^{itz} \over z^{2}+1}\,dz=\pi e^{t},}$

و نهایتاً داریم

${\displaystyle \int _{-\infty }^{\infty }{e^{itz} \over z^{2}+1}\,dz=\pi e^{-\left|t\right|}.\quad \square }$

(اگر t = ۰ آنگاه انتگرال به حسابان حقیقی مقدار منجر می‌شود که مقدار آن برابرπ است)

با جایگزینی‌های خاصی می‌توان انتگرال‌هایی رل که توابع مثلثاتی دارند، به انتگرال توابع معمولی روی یک متغیر مختلط تبدیل کرد و روش‌های بالا را برای محاسبهٔ انتگرال به کار برد.

به عنوان مثال انتگرال زیر را در نظر بگیرید

${\displaystyle \int _{-\pi }^{\pi }{1 \over 1+3(\cos {t})^{2}}\,dt.}$

باید دنبال جایگزینی z = e^itبگردیم. اکنون به یاد بیاورید که

${\displaystyle \cos {t}={1 \over 2}\left(e^{it}+e^{-it}\right)={1 \over 2}\left(z+{1 \over z}\right)}$

و

${\displaystyle {dz \over dt}=iz,\ dt={dz \over iz}.}$

اگر C را دایرهٔ واحد در نظر بگیریم، با جایگذاری خواهیم داشت:

${\displaystyle \oint _{C}{1 \over 1+3({1 \over 2}(z+{1 \over z}))^{2}}\,{dz \over iz}}$

${\displaystyle =\oint _{C}{1 \over 1+{3 \over 4}(z+{1 \over z})^{2}}{1 \over iz}\,dz=\oint _{C}{-i \over z+{3 \over 4}z(z+{1 \over z})^{2}}\,dz=-i\oint _{C}{1 \over z+{3 \over 4}z(z^{2}+2+{1 \over z^{2}})}\,dz}$

${\displaystyle =-i\oint _{C}{1 \over z+{3 \over 4}(z^{3}+2z+{1 \over z})}\,dz=-i\oint _{C}{1 \over {3 \over 4}z^{3}+{5 \over 2}z+{3 \over 4z}}\,dz}$

${\displaystyle =-i\oint _{C}{4 \over 3z^{3}+10z+{3 \over z}}\,dz=-4i\oint _{C}{1 \over 3z^{3}+10z+{3 \over z}}\,dz}$

${\displaystyle =-4i\oint _{C}{z \over 3z^{4}+10z^{2}+3}\,dz.}$

سپس از فرمول انتگرال کوشی استفاده می‌کنیم. با فاکتورگیری مخرج:

${\displaystyle =-4i\oint _{C}{z \over 3z^{4}+10z^{2}+3}\,dz=-4i\oint _{C}{z \over 3(z^{2}+3)(z^{2}+1/3)}\,dz}$

${\displaystyle =-4i\oint _{C}{z \over 3(z+{\sqrt {3}}i)\left(z-{\sqrt {3}}i\right)\left(z+{\sqrt {1 \over 3}}i\right)\left(z-{\sqrt {1 \over 3}}i\right)}\,dz}$

${\displaystyle =-{4 \over 3}i\oint _{C}{z \over (z+{\sqrt {3}}i)(z-{\sqrt {3}}i)\left(z+{\sqrt {1 \over 3}}i\right)\left(z-{\sqrt {1 \over 3}}i\right)}\,dz.}$

پس نقاط تکینی که باید در نظر گرفته شوند روی 3^−1/2I و −3^−1/2I هستند. اکنون می‌توانیم انتگرال را کاهش دهیم:

${\displaystyle =-{4 \over 3}i\oint _{C_{1}}{\,{z \over (z+{\sqrt {3}}i)(z-{\sqrt {3}}i)\left(z+{\sqrt {1 \over 3}}i\right)}\, \over \left(z-{\sqrt {1 \over 3}}i\right)}\,dz+-{4 \over 3}i\oint _{C_{2}}{\,{z \over (z+{\sqrt {3}}i)(z-{\sqrt {3}}i)\left(z-{\sqrt {1 \over 3}}i\right)}\, \over \left(z+{\sqrt {1 \over 3}}i\right)}}$

که در آن C₁ یک دایرهٔ کوچک دور 3^−1/2I، و C₂ یک دایرهٔ کوچک دور −3^−1/2i است. اکنون می‌توانیم از فرمول استفاده کنیم:

${\displaystyle =-{4 \over 3}i\left(2\pi i\left.\left({z \over (z+{\sqrt {3}}i)(z-{\sqrt {3}}i)(z+{\sqrt {1 \over 3}}i)}\right)\right|_{z={\sqrt {1 \over 3}}i}\right.}$

${\displaystyle \left.+2\pi i\left.\left({z \over (z+{\sqrt {3}}i)(z-{\sqrt {3}}i)(z-{\sqrt {1 \over 3}}i)}\right)\right|_{z=-{\sqrt {1 \over 3}}i}\right)}$

${\displaystyle =-{4 \over 3}i\left(2\pi i\left({{\sqrt {1 \over 3}}i \over ({\sqrt {1 \over 3}}i+{\sqrt {3}}i)({\sqrt {1 \over 3}}i-{\sqrt {3}}i)({\sqrt {1 \over 3}}i+{\sqrt {1 \over 3}}i)}\right)\right.}$

${\displaystyle \left.+2\pi i\left({-{\sqrt {1 \over 3}}i \over (-{\sqrt {1 \over 3}}i+{\sqrt {3}}i)(-{\sqrt {1 \over 3}}i-{\sqrt {3}}i)(-{\sqrt {1 \over 3}}i-{\sqrt {1 \over 3}}i}\right)\right)}$

${\displaystyle =-{4 \over 3}i\left(2\pi i\left({{\sqrt {1 \over 3}}i \over ({4 \over {\sqrt {3}}}i)(-{2 \over {\sqrt {3}}}i)({2 \over {\sqrt {3}}}i)}\right)+2\pi i\left({-{\sqrt {1 \over 3}}i \over ({2 \over {\sqrt {3}}}i)(-{4 \over {\sqrt {3}}}i)(-{2 \over {\sqrt {3}}}i)}\right)\right)}$

${\displaystyle =-{4 \over 3}i\left(2\pi i\left({{\sqrt {1 \over 3}}i \over i({4 \over {\sqrt {3}}})({2 \over {\sqrt {3}}})({2 \over {\sqrt {3}}})}\right)+2\pi i\left({-{\sqrt {1 \over 3}}i \over -i({2 \over {\sqrt {3}}})({4 \over {\sqrt {3}}})({2 \over {\sqrt {3}}})}\right)\right)}$

${\displaystyle =-{4 \over 3}i\left(2\pi i\left({{\sqrt {1 \over 3}} \over ({4 \over {\sqrt {3}}})({2 \over {\sqrt {3}}})({2 \over {\sqrt {3}}})}\right)+2\pi i\left({{\sqrt {1 \over 3}} \over ({2 \over {\sqrt {3}}})({4 \over {\sqrt {3}}})({2 \over {\sqrt {3}}})}\right)\right)}$

${\displaystyle =-{4 \over 3}i\left(2\pi i\left({\,{\sqrt {1 \over 3}}\, \over {16 \over 3{\sqrt {3}}}}\right)+2\pi i\left({\,{\sqrt {1 \over 3}}\, \over {16 \over 3{\sqrt {3}}}}\right)\right)}$

${\displaystyle =-{4 \over 3}i\left(2\pi i\left({3 \over 16}\right)+2\pi i\left({3 \over 16}\right)\right)=-{4 \over 3}i\left(\pi i\left({3 \over 8}+{3 \over 8}\right)\right)={4 \over 3}\left({3 \over 4}\right)\pi =\pi .\quad \square }$

انتگرال زیر را در نظر بگیرید

${\displaystyle \int _{0}^{\infty }{{\sqrt {x}} \over x^{2}+6x+8}\,dx.}$

می‌توانیم با فرموله کردن انتگرال مختلط شروع کنیم

${\displaystyle \int _{C}{{\sqrt {z}} \over z^{2}+6z+8}\,dz=I.}$

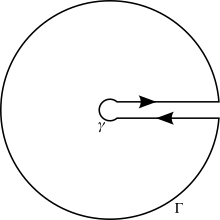
دوباره می‌توانیم برای بدست آوردن مانده مربوطه، از فرمول انتگرال‌گیری کوشی یا قضیهٔ مانده‌استفاده کنیم. با این حال، نکتهٔ مهم این است که z^1/2=e^{1/2 Log(z)}، بنا بر این z^1/2 یک برش شاخه‌ای دارد. این بر روی انتخاب مسیر تأثیر می‌گذارد. به‌طور معمول برش شاخه‌ای لگاریتم به صورت محور حقیقی منفی تعریف می‌شود، با این حال، این محاسبه انتگرال را پیچیده‌تر می‌کند، بنا بر این ما آن را به صورت محور حقیقی مثبت تعریف می‌کنیم. سپس از مسیر ی استفاده می‌کنیم که به آن سوراخ کلید گفته می‌شود، و از یک دایرهٔ کوچک دور مبدأ با شعاع ε، متصل به یک پاره خط موازی و نزدیک به محور حقیقی مثبت، و در ادامه، یک دایرهٔ تقریباً کامل که به یک پاره خط دیگر موازی و نزدیک به محور حقیقی مثبت ولی زیر آن متصل است، و در جهت منفی به دایرهٔ کوچک بازمی‌گردد، تشکیل شده‌است. اگر γ دایرهٔ کوچک به شعاع ε، و Γ دایرهٔ بزرگ به شعاع r باشد، آنگاه

${\displaystyle {\begin{aligned}\int _{C}{{\sqrt {z}} \over z^{2}+6z+8}\,dz&=&\int _{\epsilon }^{R}{{\sqrt {z}} \over z^{2}+6z+8}\,dz\\&+&\int _{\Gamma }{{\sqrt {z}} \over z^{2}+6z+8}\,dz\\&+&\int _{R}^{\epsilon }{{\sqrt {z}} \over z^{2}+6z+8}\,dz\\&+&\int _{\gamma }{{\sqrt {z}} \over z^{2}+6z+8}\,dz.\end{aligned}}}$

از آنجایی که z^1/2=e^{1/2 Log(z)}، در اروشاد مسیر زیر برش شاخه‌ای، در رابطه با Γ به ۲π رسیدیم، بنا بر این

${\displaystyle \int _{R}^{\epsilon }{{\sqrt {z}} \over z^{2}+6z+8}\,dz=\int _{R}^{\epsilon }{e^{{1 \over 2}\mathrm {Log} (z)} \over z^{2}+6z+8}\,dz=\int _{R}^{\epsilon }{e^{{1 \over 2}(\log {|z|}+i\arg {z})} \over z^{2}+6z+8}\,dz}$

${\displaystyle =\int _{R}^{\epsilon }{e^{{1 \over 2}\log {|z|}}e^{1/2(2\pi i)} \over z^{2}+6z+8}\,dz=\int _{R}^{\epsilon }{e^{{1 \over 2}\log {|z|}}e^{\pi i} \over z^{2}+6z+8}\,dz}$

${\displaystyle =\int _{R}^{\epsilon }{-{\sqrt {x}} \over x^{2}+6x+8}\,dx=-\int _{\epsilon }^{R}{-{\sqrt {x}} \over x^{2}+6x+8}\,dx}$

با ساده کردن

${\displaystyle =\int _{\epsilon }^{R}{{\sqrt {x}} \over x^{2}+6x+8}\,dx,}$

و آنگاه

${\displaystyle {\begin{aligned}\int _{C}{{\sqrt {z}} \over z^{2}+6z+8}\,dz&=&\int _{\epsilon }^{R}{{\sqrt {z}} \over z^{2}+6z+8}\,dz\\&+&\int _{\Gamma }{{\sqrt {z}} \over z^{2}+6z+8}\,dz\\&+&\int _{\epsilon }^{R}{{\sqrt {z}} \over z^{2}+6z+8}\,dz\\&+&\int _{\gamma }{{\sqrt {z}} \over z^{2}+6z+8}\,dz.\end{aligned}}}$

می‌توان نشان داد که وقتی ε به سمت صفر و R به سمت بی‌نهایت میل می‌کند، انتگرال روی Γ و γ، هر دو به سمت صفر میل می‌کنند. بنا بر این

${\displaystyle \int _{C}{{\sqrt {z}} \over z^{2}+6z+8}\,dz=2\int _{0}^{\infty }{{\sqrt {x}} \over x^{2}+6x+8}\,dx.}$

و با استفاده از قضیهٔ مانده یا فرمول انتگرال‌گیری کوشی بدست می‌آوریم

${\displaystyle \pi i\left({i \over {\sqrt {2}}}-i\right)=\int _{0}^{\infty }{{\sqrt {x}} \over x^{2}+6x+8}\,dx=\pi \left(1-{1 \over {\sqrt {2}}}\right).\quad \square }$

می‌خواهیم انتگرال زیر را محاسبه کنیم

${\displaystyle I=\int _{0}^{3}{\left(x^{3}(3-x)\right)^{1/4} \over 5-x}\,dx.}$

که احتیاج به مطالعهٔ دقیق روی تابع زیر دارد

${\displaystyle f(z)=\left(z^{3}(3-z)\right)^{1/4}.}$

طوری ${\displaystyle f(z)}$ را می‌سازیم که یک برش شاخه‌ای روی ${\displaystyle [0,3]}$ داشته باشد، که در شکل با رنگ قرمز مشخص شده‌است. برای این کار، دو شاخه از لگاریتم انتخاب می‌کنیم و قرار می‌دهیم

${\displaystyle (z^{3})^{1/4}=z^{3/4}=\exp(3/4\log(z))\quad {\mbox{where}}\quad -\pi \leq \arg(\log(z))<\pi }$

و

${\displaystyle (3-z)^{1/4}=\exp(1/4\log(3-z))\quad {\mbox{where}}\quad 0\leq \arg(\log(z))<2\pi .}$

بنا بر این برش ${\displaystyle z^{3/4}}$ برابر است با ${\displaystyle (-\infty ,0]}$و برش ${\displaystyle (3-z)^{1/4}}$ برابر است با ${\displaystyle (-\infty ,3]}$. بسیار ساده است که ببینیم که برش ضرب این دو ${\displaystyle [0,3]}$ است، چرا که ${\displaystyle f(z)}$ روی ${\displaystyle (-\infty ,0)}$ پیوسته‌است. این بدین خاطر است که وقتی ${\displaystyle z=-r<0}$ و ما از بالا به برش نزدیک می‌شویم، ${\displaystyle f(z)}$ مقدار زیر را دارد

${\displaystyle r^{3/4}\exp(3/4\pi i)(3+r)^{1/4}\exp(2/4\pi i)=r^{3/4}(3+r)^{1/4}\exp(5/4\pi i).\,}$

When we approach from below, ${\displaystyle f(z)}$ has the value

${\displaystyle r^{3/4}\exp(-3/4\pi i)(3+r)^{1/4}\exp(0/4\pi i)=r^{3/4}(3+r)^{1/4}\exp(-3/4\pi i).\,}$

ولی ${\displaystyle \exp(-3/4\pi i)=\exp(5/4\pi i)}$، و روی برش پیوستگی داریم. این در شکل مشهود است، جایی که دو دایرهٔ سیاه مقدار مربوطهٔ مبحث لگاریتم روی ${\displaystyle z^{3/4}}$ و ${\displaystyle (3-z)^{1/4}}$ علامت‌گذاری شده‌اند. از مسیر ی که در شکل با رنگ سبز نشان داده شده‌استفاده خواهیم کرد. برای این کار، باید مقدار ${\displaystyle f(z)}$ را روی خطوط بالا و پایین برش محاسبه کنیم. قرار دهید ${\displaystyle z=r}$ که ${\displaystyle 0\leq r\leq 3}$. روی پاره خط بالایی، ${\displaystyle f(z)}$ مقدار زیر را دارد

${\displaystyle r^{3/4}\exp(3/4\,0\,\pi i)(3-r)^{1/4}\exp(2/4\pi i)=i\,r^{3/4}(3-r)^{1/4}\,}$

و روی پاره خط پایینی

${\displaystyle r^{3/4}\exp(3/4\,0\,\pi i)(3-r)^{1/4}\exp(0/4\pi i)=r^{3/4}(3-r)^{1/4}\,}$

چنین بر می‌آید که انتگرال

${\displaystyle {\frac {f(z)}{5-z}}}$

روی پاره خط بالایی برابر است با −iI و روی پاره خط پایینی برابر است با I. اگر بتوانیم نشان دهیم انتگرال روی دو دایرهٔ سبز، در حد از بین می‌رود، آنگاه به وسیلهٔ قضیهٔ کوشی مانده مقدار I را هم خواهیم داشت. شعاع دایره‌های سبز را ${\displaystyle \rho }$ قرار دهید، که ${\displaystyle \rho <1/1000}$ و ${\displaystyle \rho \rightarrow 0}$، و نامساوی ML را اعمال کنید. برای دایرهٔ ${\displaystyle C_{L}}$ در سمت چپ، در می‌یابیم که

${\displaystyle \left|\int _{C_{L}}{\frac {f(z)}{5-z}}dz\right|\leq 2\pi \rho {\frac {\rho ^{3/4}(3+1/1000)^{1/4}}{5-1/1000}}\in {\mathcal {O}}\left(\rho ^{7/4}\right)\rightarrow 0.}$

متشابها برای دایرهٔ ${\displaystyle C_{R}}$ در سمت راست داریم

${\displaystyle \left|\int _{C_{R}}{\frac {f(z)}{5-z}}dz\right|\leq 2\pi \rho {\frac {(3+1/1000)^{3/4}\rho ^{1/4}}{2-1/1000}}\in {\mathcal {O}}\left(\rho ^{5/4}\right)\rightarrow 0.}$

اکنون با استفاده از قضیهٔ کوشی redsidue داریم

${\displaystyle (1-i)I=-2\pi i\left(\mathrm {Res} _{z=5}{\frac {f(z)}{5-z}}+\mathrm {Res} _{z=\infty }{\frac {f(z)}{5-z}}\right).}$

با استفاده از شاخهٔ لگاریتم از محاسبات قبل، به وضوح داریم

${\displaystyle \mathrm {Res} _{z=5}{\frac {f(z)}{5-z}}=-5^{3/4}\exp(1/4\log(-2)).}$

در شکل، قطب با رنگ آبی مشخص شده‌است. مقدار بالاها شکل زیر ساده می‌شود

${\displaystyle -5^{3/4}\exp(1/4(\log(2)+\pi i))=-\exp(1/4\pi i)5^{3/4}2^{1/4}.\,}$

از فرمول زیر برای مانده در بی‌نهایت استفاده می‌کنیم

${\displaystyle \mathrm {Res} _{z=\infty }h(z)=\mathrm {Res} _{z=0}-{\frac {1}{z^{2}}}h\left({\frac {1}{z}}\right).}$

با جایگذاری داریم

${\displaystyle 1/(5-1/z)=-z\left(1+5z+5^{2}z^{2}+5^{3}z^{3}+\cdots \right)}$

و

${\displaystyle \left(1/z^{3}(3-1/z)\right)^{1/4}=1/z\,(3z-1)^{1/4}=1/z\exp(1/4\pi i)(1-3z)^{1/4},}$

که از این حقیقت استفاده کرده‌ایم که برای دومین شاخهٔ لگاریتم،${\displaystyle -1=\exp(\pi i)}$. سپس با به کار بردن بسط دو جمله‌ای داریم

${\displaystyle 1/z\exp(1/4\pi i)\left(1-{1/4 \choose 1}3z+{1/4 \choose 2}3^{2}z^{2}-{1/4 \choose 3}3^{3}z^{3}+\cdots \right).}$

نتیجه بدین صورت است

${\displaystyle \mathrm {Res} _{z=\infty }{\frac {f(z)}{5-z}}=\exp(1/4\pi i)(5-3/4)=\exp(1/4\pi i)17/4.}$

نهایتاً مقدار I به صورت زیر به دست می‌آید

${\displaystyle I=-2\pi i\,{\frac {\exp(1/4\pi i)}{1-i}}\left(17/4-5^{3/4}2^{1/4}\right)=-2\pi i\,2^{-1/2}i\left(17/4-5^{3/4}2^{1/4}\right)}$

که برابر است با

${\displaystyle I={\frac {\pi }{2{\sqrt {2}}}}\left(17-5^{3/4}2^{9/4}\right)={\frac {\pi }{2{\sqrt {2}}}}\left(17-40^{3/4}\right).}$