انتگرال لبگ
در ریاضیات، انتگرال یک تابع نامنفی تک متغیره را میتوان در سادهترین حالت، مساحت بین نمودار تابع و محور ایکسها در نظر گرفت. انتگرال لبگ مفهوم انتگرالگیری را به دسته بزرگتری از توابع گسترش میدهد. همچنین این نوع انتگرالگیری دامنه ای که این توابع بر روی آنها انتگرالگیری میشوند را نیز گسترش میدهند.در روش انتگرال گیری ریمان،بازه های انتگرال پذیری به تعدادی متناهی زیر بازه تقسیم می شد در روش لبگ به مجموعه های کلی تری به نام مجموعه های اندازه پذیر تقسیم می شوند.
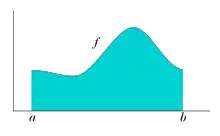
خیلی قبل تر از قرن بیستم، ریاضیدانان میدانستند که برای توابع نا منفی که نمودار آن به اندازه کافی هموار باشد، مثل توابع پیوسته بر روی بازههای کراندار بسته، مساحت زیر نمودار را میتوان با کمک روشهای تقریب زدن با چند ضلعیها حساب کرد. با این حال همچنان که توجهات بیشتری به سمت توابع نامنظم تر جلب شد (به عنوان مثال توابعی که از فرایند حد گیری در نظریه احتمال آنالیز ریاضی بهوجود میآیند)، بیش از پیش مشخص شد که برای تعریف انتگرالگیری از چنین توابعی، نیاز به تکنیکهای تقریب محتاطانه تری وجود دارد. همچنین ممکن است بخواهیم بر روی فضاهایی کلی تر از خط حقیقی انتگرالگیری کنیم. انتگرال لبگ تجریدهای لازم برای این کار مهم را فراهم میآورد.
انتگرال لبگ نقش مهمی را در نظریه احتمالات، آنالیز حقیقی، و بسیاری دیگر از زمینههای علوم ریاضی بازی میکند. این انتگرال به افتخار هنری لبگ (۱۸۷۵–۱۹۴۱) نامگذاری شده که آن را در ۱۹۰۴ معرفی کرد.(Lebesgue 1904)
اصطلاح انتگرالگیری لبگ میتواند هم به معنی نظریه کلی انتگرالگیری توابع با توجه به یک اندازه کلی معرفی شده توسط لبگ باشد، یا در حالت خاص تر همان انتگرالگیری توابع روی بخشی از اعداد حقیقی با توجه به اندازه لبگ.
معرفی
انتگرال یک تابع مثبت مانند بین کران های و را میتوان به عنوان مساحت زیر نمودار تفسیر کرد. فهم این مطلب برای توابع ساده ای چون چند جمله ایها راحت است، اما در مورد توابع نامتعارف تر چطور؟ در کل، برای چه دسته از توابعی «مساحت زیر نمودار» معنا دارد؟ جواب این سؤال اهمیت نظری و عملی بالایی دارد.
ریاضیدانان در قرن نوزدهم میلادی تلاش کردند تا حساب انتگرالی را به عنوان بخشی از حرکت عمومی به سمت دقت و استحکام ریاضیاتی (Rigor) بر روی بنیان های مستحکمی بنا کنند. انتگرال ریمانی که توسط برنهارد ریمان (۱۸۲۶-۱۸۶۶) پیشنهاد شد، یک تلاش موفقیت آمیز گسترده در جهت ارائه چنین بنیانی بود. تعریف ریمان با ساخت دنباله ای از مساحتها شروع می کند که به راحتی قابل محاسبه اند و جمعشان به انتگرال تابع داده شده همگرا می باشد. این تعریف ازین لحاظ موفق است که برای بسیاری از مسائل از قبل حل شده جواب مورد انتظار را ایجاد کرده و نتایج مفیدی را برای بسیاری از مسائل دیگر ارائه می کند.
با این حال، انتگرال ریمانی به خوبی با دنباله توابع برهمکنش ندارد و تحلیل چنین دنباله هایی را دچار مشکل می کند. این نکته به عنوان مثال در مطالعه سری فوریه، تبدیل فوریه و دیگر موضوعات اهمیت دارد. انتگرال لبگ قادر است تا توصیف کند چه زمان و چگونه امکان حد گیری زیر نماد انتگرال گیری ممکن است (این حد گیری از طریق قضایای قدرتمند همگرایی یکنواخت و همگرایی تسلطی انجام می شود).
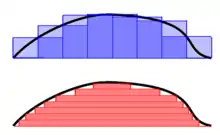
در حالی که انتگرال ریمانی مساحت زیر نمودار را از طریق مستطیل های عمودی محاسبه می کند، تعریف لبگ ورقه های افقی را در نظر می گیرد که لزوماً مستطیل نیستند و انعطاف بیشتری دارند. به همین دلیل تعریف لبگ امکان محاسبه انتگرال را برای دسته گسترده تری از توابع فراهم می آورد. به عنوان مثال، تابع دیریکله که برای اعداد گنگ ۰ و برای اعداد گویا ۱ است، دارای انتگرال لبگ است اما انتگرال ریمان ندارد. به علاوه، انتگرال لبگ این تابع صفر است که با شهود هم مطابقت دارد، چرا که شهود به ما می گوید هنگامی که عددی از اعداد حقیقی را انتخاب می کنیم احتمال گویا بودنش صفر است.
لبگ رهیافت خود به انتگرال گیری را در نامه ای به پاول مونتل اینگونه بیان می دارد:
من باید مبلغ خاصی را پرداخت کنم، مبلغی که آن را در جیب خودم جمع آوری نمودم. اسکناس ها و سکه ها را به ترتیبی که در جیبم می یابم از آن خارج کرده و آن ها را به طلبکار می دهم تا کل مبلغ تصفیه شود. این توصیف انتگرال ریمانی بود. اما می توانستم به روش دیگری هم جلو روم. بعد از این که تمام پول خود را از جیبم در آوردم اسکناس ها و سکه ها را به گونه ای مرتب می کنم تا مطابق با مبلغ بدهی ام شود و آنگاه کپه های مختلف از آن ها را یکی پس از دیگری به طلبکارم پرداخت می کنم. این روش انتگرال گیری من است.
دیدگاه مورد نظر او این است که باید بتوان مقادیر تابع را آزادانه بازآرایی کرد، در حالی که مقدار انتگرال هم حفظ شده و تغییری نکند. فرایند بازآرایی قادر به تبدیل یک تابع آسیبشناختی (پاتولوژیکال، غیر عادی) به تابعیست که از نقطه نظر انتگرال گیری به میزان کافی "خوب" بوده و ازین رو امکان می دهد که بدین طریق بتوانیم از توابع آسیبشناختی بهتر انتگرال گیری کنیم.
تفسیر شهودی
برای این که به رهیافت های مختلف انتگرال گیری شهود پیدا کنیم، اجازه دهید تا تصور کنیم که می خواهیم حجم یک کوه (بالاتر از سطح دریا) را بدست آوریم.
- رهیافت ریمان-داربوکس
- قاعده کوه را به مشبکه ای با مربع هایی که اضلاع یک متری دارند تقسیم بندی کنید. ارتفاع کوه را در مرکز هر مربع بدست آورید. آنگاه حجم یکی از مربع های این مشبکه تقریباً این است که در آن ارتفاع آن مربع خاص می باشد، چنان که حجم کل برابر ۱ متر مربع ضرب در جمع کل ارتفاع مربع ها خواهد بود.
- رهیافت لبگ
- یک نگاشت خط تراز از کوه رسم کنید، به گونه ای که خطوط تراز مجاور اختلاف ارتفاع یک متری از هم داشته باشند. حجمی که یک تراز خاص آن را در بر می گیرد تقریباً برابر است که در آن مساحت تراز مورد نظر است، چنان که حجم کل برابر جمع کل مساحت تراز ها ضرب در ۱ متر می باشد.
فولند تفاوت بین رهیافت انتگرال گیری ریمانی و لبگ را اینگونه بیان می دارد: "برای محاسبه انتگرال ریمانی ، دامنه به زیر بازه هایی افراز می شود"، در حالی که در انتگرال لبگ، "در عمل برد افراز می شود."[1]
به سوی یک تعریف صوری
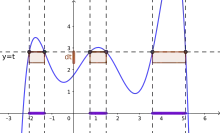
برای تعریف انتگرال لبگ، نیازمند به مفهوم صوری اندازه هستیم، که می توان گفت به طور کلی و نادقیق به هر مجموعه از اعداد حقیقی، عدد نامنفی را که نشان دهنده "اندازه" است را نسبت می دهد. این مفهوم "اندازه" باید با مفهوم رایج طول یک بازه یا اجتماع مجزای بازه ها سازگاری داشته باشد. فرض کنید که یک تابع حقیقی مقدار نا-منفی باشد. با استفاده از فلسفهی "افراز در برد "، انتگرال باید برابر با جمع روی مساحت مقدماتی مشمول در نوار افقی باریک بین و باشد.
این مساحت مقدماتی همان مقدار زیر است:
فرض کنید:
آنگاه انتگرال لبگ به این صورت تعریف خواهد شد:[2]
که در آن انتگرال سمت راست یک انتگرال ریمانی ناسره معمولیست. توجه کنید که یک تابع نا-منفی نزولیست و لذا یک انتگرال ریمانی ناسره خوش تعریف دارد که مقدار آن در بازه قرار می گیرد. برای دسته مناسبی از توابع (توابع اندازه پذیر)، این منجر به تعریف انتگرال لبگ می شود.
یک تابع اندازه پذیر (که لزوماً مثبت نیست) لبگ انتگرال پذیر است اگر مساحت بین نمودار و محور متناهی باشد:
در این حالت، همانند حالت ریمانی، انتگرال برابر تفاضل بین مساحت بالای محور و مساحت زیر محور خواهد بود:
که در آن تجزیه به تفاضل دو تابع نامنفی است که به صورت زیر می باشند:
قضیه همگرایی یکنوای لبگ
این قضیه بیان میکند، اگر سری صعودی از توابع اندازهپذیر موجود باشد، آنگاه انتگرال حد این توابع برابر با حد انتگرال تابعی است که به وسیلهی سری صعودی تقریب زده شده است.
یادداشتها
- Folland, Gerald B. (1984). Real Analysis: Modern Techniques and Their Applications. Wiley. p. 56.
- Lieb & Loss 2001
منابع
- Bartle, Robert G. (1995). The elements of integration and Lebesgue measure. Wiley Classics Library. New York: John Wiley & Sons Inc. xii+179. ISBN 0-471-04222-6. MR 1312157.
- Bauer, Heinz (2001). Measure and Integration Theory. De Gruyter Studies in Mathematics 26. Berlin: De Gruyter. 236. ISBN 978-3-11-016719-1.
- Bourbaki, Nicolas (2004). Integration. I. Chapters 1–6. Translated from the 1959, 1965 and 1967 French originals by Sterling K. Berberian. Elements of Mathematics (Berlin). Berlin: Springer-Verlag. xvi+472. ISBN 3-540-41129-1. MR 2018901.
- Dudley, Richard M. (1989). Real analysis and probability. The Wadsworth & Brooks/Cole Mathematics Series. Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software. xii+436. ISBN 0-534-10050-3. MR 0982264. Very thorough treatment, particularly for probabilists with good notes and historical references.
- Folland, Gerald B. (1999). Real analysis: Modern techniques and their applications. Pure and Applied Mathematics (New York) (Second ed.). New York: John Wiley & Sons Inc. xvi+386. ISBN 0-471-31716-0. MR 1681462.
- Halmos, Paul R. (1950). Measure Theory. New York, N. Y.: D. Van Nostrand Company, Inc. pp. xi+304. MR 0033869. A classic, though somewhat dated presentation.
- "Lebesgue integral", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Lebesgue, Henri (1904). "Leçons sur l'intégration et la recherche des fonctions primitives". Paris: Gauthier-Villars.
- Lebesgue, Henri (1972). Oeuvres scientifiques (en cinq volumes) (به French). Geneva: Institut de Mathématiques de l'Université de Genève. p. 405. MR 0389523.
- Lieb, Elliott; Loss, Michael (2001). Analysis. Graduate Studies in Mathematics. 14 (2nd ed.). American Mathematical Society. ISBN 978-0-8218-2783-3.
- Loomis, Lynn H. (1953). An introduction to abstract harmonic analysis. Toronto-New York-London: D. Van Nostrand Company, Inc. pp. x+190. MR 0054173. Includes a presentation of the Daniell integral.
- Munroe, M. E. (1953). Introduction to measure and integration. Cambridge, Mass.: Addison-Wesley Publishing Company Inc. pp. x+310. MR 0053186. Good treatment of the theory of outer measures.
- Royden, H. L. (1988). Real analysis (Third ed.). New York: Macmillan Publishing Company. pp. xx+444. ISBN 0-02-404151-3. MR 1013117.
- Rudin, Walter (1976). Principles of mathematical analysis. International Series in Pure and Applied Mathematics (Third ed.). New York: McGraw-Hill Book Co. pp. x+342. MR 0385023. Known as Little Rudin, contains the basics of the Lebesgue theory, but does not treat material such as Fubini's theorem.
- Rudin, Walter (1966). Real and complex analysis. New York: McGraw-Hill Book Co. pp. xi+412. MR 0210528. Known as Big Rudin. A complete and careful presentation of the theory. Good presentation of the Riesz extension theorems. However, there is a minor flaw (in the first edition) in the proof of one of the extension theorems, the discovery of which constitutes exercise 21 of Chapter 2.
- Saks, Stanisław (1937). "Theory of the Integral". Monografie Matematyczne. 7 (2nd ed.). Warszawa- Lwów: G.E. Stechert & Co.: VI+347. JFM 63.0183.05. Zbl 0017.30004.. English translation by Laurence Chisholm Young, with two additional notes by Stefan Banach.
- Shilov, G. E.; Gurevich, B. L. (1977). Integral, measure and derivative: a unified approach. Translated from the Russian and edited by Richard A. Silverman. Dover Books on Advanced Mathematics. New York: Dover Publications Inc. xiv+233. ISBN 0-486-63519-8. MR 0466463. Emphasizes the Daniell integral.
- Siegmund-Schultze, Reinhard (2008), "Henri Lebesgue", in Timothy Gowers, June Barrow-Green, Imre Leader, Princeton Companion to Mathematics, Princeton University Press.
- Teschl, Gerald. Topics in Real and Functional Analysis. (lecture notes).
- Yeh, James (2006). Real Analysis: Theory of Measure and Integral 2nd. Edition Paperback. Singapore: World Scientific Publishing Company Pte. Ltd. p. 760. ISBN 978-981-256-6.
- مشارکتکنندگان ویکیپدیا. «Lebesgue Integration». در دانشنامهٔ ویکیپدیای انگلیسی.
