انتگرال ریمان
انتگرال ریمان، در آنالیز حقیقی، اولین تعریف دقیق از انتگرال تابع در یک بازه شناخته میشود. این تعریف را برنهارت ریمان ارائه داد. گرچه انتگرال ریمان دارای محدودیتهایی برای بسیاری از مسائل تئوری است، ولی یکی از سادهترین روشهای تعریف انتگرال بوده و بهطور گستردهای بکار میرود.
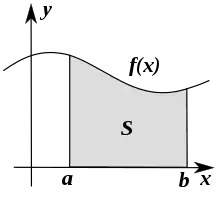
انتگرال سطح زیر یک منحنی در بازه [a,b].
تعریف انتگرال ریمان

دنبالهای از مجموع ریمان. عدد نمایش داده شده در بالای شکل، سمت راست، برابر با مجموع مساحت مستطیلهای خاکستری است. این مجموع به مقدار انتگرال تابع میل میکند.
تقسیم بازه
تقسیم بازه [a,b] یک دنباله متناهی به صورت است، که هر یک زیربازه نامیده میشود. اندازه چنین تقسیمی برابر است با طول طولانیترین زیربازه، یعنی: ، .
جستارهای وابسته
منابع
مشارکتکنندگان ویکیپدیا. «Riemann integral». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۱۵ فوریه ۲۰۰۸.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
