تابع مقعر

تابع کاو[1] یا تابع مقعّر تابعی است که اگر دو نقطهٔ دلخواه $A$ و $B$ از این تابع را در نظر بگیریم، خط $AB$ همواره زیر تابع یا همسطح آن قرار بگیرد. به بیان ریاضی:

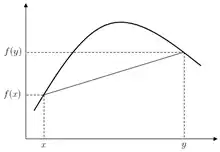
f[\alpha x_{1}+(1-\alpha )x_{2}]\geq \alpha f(x_{1})+(1-\alpha )f(x_{2})

یک تابع کاو

اگر در این نابرابری، علامت ≤ را با علامت <جایگزین کنیم، تعریف تابع اکیداً کاو به دست می‌آید. با توجه به تعریف هر خط راستی هم نمایانگر یک تابع کوژ و هم نمایانگر یک تابع کاو است.

ویژگی‌ها

برخی از ویژگی‌های تابع کاو از این قرارند:[2]

مشتق دوم یک تابع کاو کوچکتر از صفر است.
بیشینهٔ موضعی یک تابع کاو، بیشینهٔ فراموضعی آن نیز هست.
تابع مجموع یک تابع (اکیداً) کاو، (اکیداً) کاو است.
اگر $f(x)$ ‎ یک تابع کاو باشد،‎ $-f(x)$ ‎ یک تابع کوژ خواهد بود.
به طور کلی اگر f(x)‎ یک تابع کاو و $\alpha$ یک مقدار ثابت باشد، در صورت مثبت بودن آلفا، $\alpha f(x)$ یک تابع کاو خواهد بود و در صورتی که $\alpha$ کوچکتر از صفر باشد ‎ $\alpha f(x)$ ‎ یک تابع کوژ خواهد بود.

جستارهای وابسته

منابع

«از اصطلاحات مورد استفادهٔ پژوهشکدهٔ آمار». بایگانی‌شده از اصلی در ۱۸ فوریه ۲۰۱۴. دریافت‌شده در ۲۱ اکتبر ۲۰۱۴.
Majumdar and Mujumdar, Water Resources Systems, 11.

Majumdar, V.; Mujumdar, S.V.P.P. (2005). Water Resources Systems. Civil engineering series. Tata McGraw-Hill. ISBN 978-0-07-059089-2. Retrieved 2014-10-21.

حسابان
پیش حسابان	بسط دوجمله‌ای تابع مقعر تابع پیوسته فاکتوریل تفاضل محدود متغیر آزاد و متغیر پابند نمودار تابع Linear function رادیان قضیه رول Secant شیب مماس
حد (ریاضی)	شکل نامعلوم حد تابع حد یک-طرفه حد دنباله مرتبه تخمین (ε, δ)-definition of limit
حساب دیفرانسیل	مشتق دیفرانسیل (ریاضیات) معادله دیفرانسیل عملگر دیفرانسیلی قضیه مقدار میانگین نمادگذاری‌های مشتق Leibniz's notation نمادگذاری‌های مشتق قواعد دیفرانسیل گیری linearity Power قواعد دیفرانسیل گیری قاعده زنجیری قاعده هوپیتال قاعده ضرب General Leibniz's rule قاعده خارج قسمت Other techniques تابع ضمنی Inverse functions and differentiation Logarithmic derivative Related rates نقاط مانا First derivative test Second derivative test Extreme value theorem بیشینه و کمینه کاربرد های دیگر روش نیوتن قضیه تیلور
انتگرال	پاد مشتق طول قوس انتگرال Constant of integration Differentiation under the integral sign قضیه اساسی حسابان Differentiating under the integral sign انتگرال‌گیری جزء به جزء Integration by substitution جانشینی مثلثاتی تغییر متغیر اویلر Weierstrass Partial fractions in integration Quadratic integral قانون ذوزنقه حجم‌ها Washer method روش پوسته
حساب برداری	مشتق‌ها تاو (ریاضی) مشتق جهت‌دار دیورژانس گرادیان عملگر لاپلاس قضایای پایه‌ای قضیه گرادیان قضیه گرین Stokes' قضیه دیورژانس
حساب چندمتغیره	قضیه دیورژانس Geometric ماتریس هسین ماتریس ژاکوبی ضرایب لاگرانژ انتگرال خطی حساب ماتریس‌ها انتگرال چندگانه مشتق جزئی انتگرال سطحی انتگرال حجمی مباحث پیشرفته Differential forms Exterior derivative قضیه استوکس Tensor calculus
دنباله و سری	Arithmetico–geometric sequence انواع سری Alternating سری دو جمله‌ای سری فوریه سری هندسی سری هارمونیک سری (ریاضیات) سری توانی بسط تیلور بسط تیلور Telescoping آزمون‌های همگرایی Abel's Alternating series Cauchy condensation Direct comparison Dirichlet's Integral Limit comparison آزمون نسبت Root آزمون جمله
توابع خاص و اعداد	عدد برنولی E (عدد) تابع نمایی لگاریتم طبیعی تقریب استرلینگ
تاریخچه حسابان	Adequality بروک تیلور کولین مک‌لورین Generality of algebra گوتفرید لایبنیتس بی‌نهایت کوچک حسابان آیزاک نیوتن Fluxion Law of Continuity لئونارد اویلر Method of Fluxions The Method of Mechanical Theorems
لیست‌ها	قواعد دیفرانسیل گیری فهرست انتگرال تابع‌های نمایی فهرست انتگرال‌های تابع‌های هیپربولیک فهرست انتگرال تابع‌های وارون هذلولوی فهرست انتگرال توابع وارون مثلثاتی فهرست انتگرال تابع‌های گنگ فهرست انتگرال‌های توابع لگاریتمی فهرست انتگرال توابع گویا فهرست انتگرال توابع مثلثاتی Secant Secant cubed فهرست حدها فهرست‌های انتگرال‌ها
موضوعات متفرقه	هندسهٔ دیفرانسیل انحنا of curves of surfaces Euler–Maclaurin formula Gabriel's Horn برهان بزرگتر بودن ۲۲/۷ از عدد پی Regiomontanus' angle maximization problem Steinmetz solid

آنالیز محدب و آنالیز تغییرات
موضوعات (فهرست)	Choquet theory بهینه‌سازی محدب دوگانگی (بهینه‌سازی) ضرایب لاگرانژ Legendre transformation Locally convex topological vector space سادک
نگاشت‌ها	تابع مزدوج محدب تابع مقعر (Closed K- Logarithmically Proper Pseudo- تابع شبه‌محدب) تابع محدب Invex function Legendre transformation تابع نیم‌پیوسته Subderivative
نتایج اصلی (فهرست)	Fenchel–Moreau theorem تابع مزدوج محدب نابرابری ینسن Hermite–Hadamard inequality Krein–Milman theorem Mazur's lemma Robinson-Ursescu Simons Ursescu
مجموعه‌ها	پوش محدب (Pseudo-) مجموعه محدب Effective domain اپی گراف Hypograph Zonotope
سری‌ها	Convex series related ((cs, lcs)-closed, (cs, bcs)-complete, (lower) ideally convex, (Hx), and (Hwx))

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.