تابع دلتای دیراک
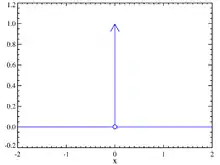
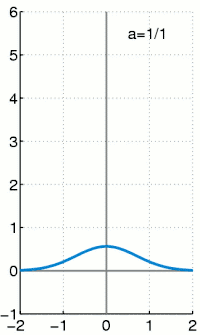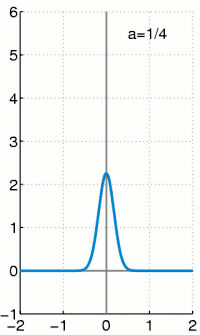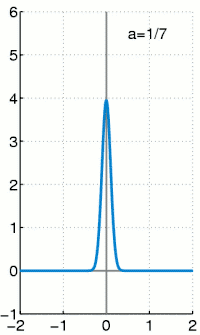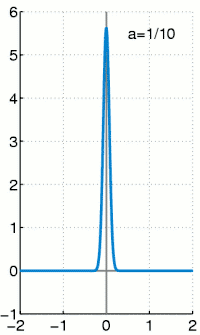
در ریاضیات و علوم، تابع دلتای دیراک، یا تابع ، یک تابع تعمیمیافته، یا توزیع، روی محور اعداد حقیقی است که همه جا مقدار صفر دارد به جز در صفر، و روی کل محور حقیقی انتگرالی با مقدار یک دارد.[1][2][3] تابع دلتا را گاهی به این صورت در نظر می گیرند: تابعی فرضی که منحنی اش در مرکز مختصات میخی بهطور نامحدود بلند، و بهطور نامحدود باریک است، با مساحت کل برابر با یک در زیر میخ، و از لحاظ فیزیکی نمایان گر یک جرم نقطهای یا بار نقطهای ایده آل شده.
این تابع شکل خاصی از ضربهٔ واحد است که اولین بار توسط فیزیکدان انگلیسی پاول دیراک مطرح شد و به نام او نامگذاری گردید.
این تابع که با حرف یونانی دلتا نمایش داده میشود، در نقطهٔ مقداری برابر بینهایت و در دیگر نقاط مقداری برابر با صفر دارد و در نتیجه انتگرال آن نیز روی بازهٔ منفی بینهایت تا مثبت بینهایت برابر یک خواهد بود.
باید توجه داشت که تابع دلتا با وجود اینکه با عنوان تابع خوانده میشود، در مفهوم، تابع نیست و بیشتر به یک تابع توزیع که در علم آمار کاربرد دارد، شبیهاست. بهعنوان مثال ضربهٔ یک چوب بیسبال به توپ در زمان کوتاهی که میتوان آن را صفر محسوب کرد، وارد میشود. در نتیجه در این زمان نیروی واردشده به توپ به صورت یک تابع ظاهر نمیشود.
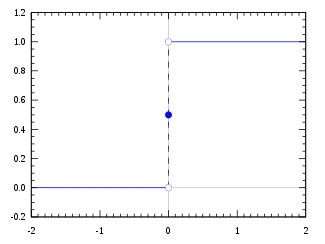
تابع دلتا مشتق تابع پلهای هویساید محسوب گردد.
تعریف
دلتای دیراک را با اغماض میتوان چنین تعریف کرد:
از تبعات این تعریف یکی این است که:
خواص
خواص جبری
حاصل ضرب توزیعی δ با x برابر با صفر است:
و بالعکس اگر (xf(x) = xg(x، که f و g توزیع هستند، آن گاه:
به ازای عدد ثابت c ای.
انتقال
انتگرال تابع دیراک تحت تاخیر زمانی را، این رابطه میدهد:
که گاهی اوقات به عنوان خاصیت غربال کردن (به انگلیسی: sifting)[4] یا خاصیت نمونه برداری (به انگلیسی: sampling) به آن اشاره میشود. گفته میشود که تابع دلتا مقدار را در نقطه t = T "غربال" میکند.
دلتای دیراک تعمیم یافته
بهطور کلی می دانیم:
که در آن تابع پله واحد است. سپس با استفاده از قاعده زنجیره ای داریم:
که در آن به صورت زیر است:
منابع
- Dirac 1958, §15 The δ function, p. 58
- Gel'fand & Shilov 1968, Volume I, §§1.1, 1.3
- Schwartz 1950, p. 3
- Weisstein, Eric W. "Sifting Property". MathWorld.
- Eric W. Weisstein et al. "Delta Function", From MathWorld--A Wolfram Web Resource.
- Eric W. Weisstein et al. "Generalized Function", From MathWorld--A Wolfram Web Resource.
