مشتق توابع مثلثاتی

دایره به مرکز O و شعاع r

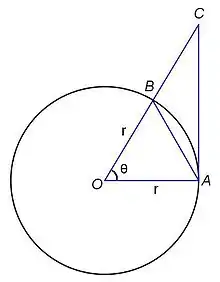
نمودار سمت چپ، یک دایره به مرکز O و شعاع r را نشان می‌دهد. زاویه θ در مرکز دایره قرار دارد و از دو شعاع OA و OB ساخته شده‌است. از آن‌جایی که می‌خواهیم θ را به سمت صفر میل دهیم، آن را یک مقدار کوچک مثبت در نظر می‌گیریم.

اکنون دو مثلث OAB و OAC و قطاع دایره‌ای OAB بین آن‌ها را در نظر می‌گیریم. از روی شکل به سادگی می‌توان گفت که نامعادله زیر بین مساحت این سه شکل برقرار است:

مساحت مثلث OAB <مساحت قطاع OAB <مساحت مثلث OAC.

برپایه تابع‌های مثلثاتی، مساحت مثلث‌ها به دست می‌آید:

• مثلث OAB (کوچک): ۱/۲ ||OA||. ||OB|| .sinθ = ۱/۲ r^۲ .sinθ
• مثلث OAC (بزرگ): ۱/۲ ||OA||. ||AC|| = ۱/۲ r. r.tanθ = ۱/۲ r^۲ .tanθ

مساحت قطاع OAB که روبرو به زاویه θ است، نیز برابر است با ۱/۲ θr^۲.

با جایگذاری مقادیر بالا در نامعادله، داریم:

۱/۲ r^۲.sinθ <۱/۲ r^۲. θ <۱/۲ r^۲.tanθ.

از آن‌جایی که شعاع دایره بزرگتر از صفر است، می‌توان طرف‌های نامعادله را بر r^۲ تقسیم کرد. هم‌چنین با توجه به این که زاویه θ بزرگ‌تر از صفر است، سینوس آن نیز بزرگ‌تر از صفر می‌باشد و می‌توان طرف‌های نامعادله را بر sinθ نیز تقسیم کرد؛ بنابراین، نامعادله به صورت زیر در می‌آید:

۱ <θ/sinθ <۱/cosθ ⇒ ۱> sinθ/θ> cosθ

در نامعادله دوم خط بالا، طرف‌های نامعادله معکوس شدند و از آن‌جایی که هر سه طرف مثبت هستند، پس از معکوس کردن، علامت نامساوی نیز عکس می‌شود. اگر از این نامعادله را در نزدیکی صفر حد بگیریم:

• طرف سمت چپ نامعادله مقدار ثابت یک است.
• طرف راست نامعادله، cos(θ) است که با نزدیک شدن به صفر، مقدار آن به یک میل می‌کند.

اکنون با استفاده از قضیه فشردگی، می‌توان حد sin x/x در x→۰ را به دست آورد. از آن‌جایی که این تابع بین دو تابع دیگر قرار دارد که حد هر دو در صفر، برابر یک است، پس حد این تابع نیز برابر با یک خواهد بود:

${\displaystyle \lim _{\theta \to 0^{+}}{\tfrac {\sin \theta }{\theta }}=1}$.

برای مقدارهای منفی نزدیک به صفر نیز می‌توان از ویژگی فرد بودن تابع سینوس استفاده کرد:

${\displaystyle \lim _{\theta \to 0^{-}}{\tfrac {\sin \theta }{\theta }}=\lim _{\theta \to 0^{+}}{\tfrac {\sin(-\theta )}{-\theta }}=\lim _{\theta \to 0^{+}}{\tfrac {-\sin \theta }{-\theta }}=\lim _{\theta \to 0^{+}}{\tfrac {\sin \theta }{\theta }}=1}$.

در این بخش، از نتیجه بخش پیشین استفاده می‌شود. برخلاف سینوس، کسینوس در نزدیکی صفر، همواره مثبت است؛ بنابراین علامت θ در محاسبه، اهمیتی ندارد.

${\displaystyle \lim _{\theta \to 0}\left({\tfrac {\cos \theta -1}{\theta }}\right)=\lim _{\theta \to 0}\left[\left({\tfrac {\cos \theta -1}{\theta }}\right)\left({\tfrac {\cos \theta +1}{\cos \theta +1}}\right)\right]=\lim _{\theta \to 0}\left({\tfrac {\cos ^{2}\theta -1}{\theta (\cos \theta +1)}}\right)}$.

اتحاد sin^۲θ + cos^۲θ = ۱ را می‌توان به صورت cos^۲θ - ۱ = -sin^۲θ نیز نوشت؛ بنابراین با دانستن این که حد حاصل‌ضرب با حاصل‌ضرب حدها برابر است، حد بالا به صورت زیر در می‌آید:

${\displaystyle \lim _{\theta \to 0}\left({\tfrac {\cos \theta -1}{\theta }}\right)=\lim _{\theta \to 0}\left({\tfrac {-\sin ^{2}\theta }{\theta (\cos \theta +1)}}\right)=\lim _{\theta \to 0}\left({\tfrac {-\sin \theta }{\theta }}\right)\times \lim _{\theta \to 0}\left({\tfrac {\sin \theta }{\cos \theta +1}}\right)=(-1)\times {\frac {0}{2}}=0}$.

با بهره گرفتن از حد تابع سینوس، فرد بودن تابع تانژانت و این که حد حاصل‌ضرب با حاصل‌ضرب حدها برابر است، داریم:

${\displaystyle \lim _{\theta \to 0^{-}}{\tfrac {\tan \theta }{\theta }}=\lim _{\theta \to 0^{+}}{\tfrac {\tan \theta }{\theta }}=\lim _{\theta \to 0}{\tfrac {\tan \theta }{\theta }}=\lim _{\theta \to 0}{\tfrac {\sin \theta }{\theta }}\times \lim _{\theta \to 0}{\tfrac {1}{\cos \theta }}=1\times 1=1}$.

برای به دست آوردن مشتق تابع سینوس، از تعریف مشتق استفاده می‌کنیم:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\sin \theta =\lim _{\delta \to 0}\left({\tfrac {\sin(\theta +\delta )-\sin \theta }{\delta }}\right)}$.

با استفاده از اتحاد جمع دو زاویه (sin(α+β) = sin α cos β + sin β cos α) داریم:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\sin \theta =\lim _{\delta \to 0}\left({\tfrac {\sin \theta \cos \delta +\sin \delta \cos \theta -\sin \theta }{\delta }}\right)=\lim _{\delta \to 0}\left[\left({\tfrac {\sin \delta }{\delta }}\cos \theta \right)+\left({\tfrac {\cos \delta -1}{\delta }}\sin \theta \right)\right]}$.

با استفاده از حد تابع‌های سینوس و کسینوس (که بالاتر، اثبات شده‌اند):

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\sin \theta =(1\times \cos \theta )+(0\times \sin \theta )=\cos \theta }$.

برای محاسبه مشتق تابع کسینوس، از تعریف مشتق به صورت زیر بهره می‌بریم:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\cos \theta =\lim _{\delta \to 0}\left({\tfrac {\cos(\theta +\delta )-\cos \theta }{\delta }}\right)}$.

با سود بردن از اتحاد cos(α+β) = cos α cos β – sin α sin β داریم:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\cos \theta =\lim _{\delta \to 0}\left({\tfrac {\cos \theta \cos \delta -\sin \theta \sin \delta -\cos \theta }{\delta }}\right)=\lim _{\delta \to 0}\left[\left({\tfrac {\cos \delta -1}{\delta }}\cos \theta \right)-\left({\tfrac {\sin \delta }{\delta }}\sin \theta \right)\right]}$.

با استفاده از حد تابع‌های سینوس و کسینوس (که بالاتر، اثبات شده‌اند):

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\cos \theta =(0\times \cos \theta )-(1\times \sin \theta )=-\sin \theta }$.

برای بهره بردن از قاعده زنجیری در محاسبه مشتق تابع کسینوس، از مشتق تابع سینوس (که بالاتر به دست آمده) و اتحاد زیر استفاده می‌کنیم:

${\displaystyle \cos \theta =\sin \left(\theta +{\tfrac {\pi }{2}}\right)}$.

با مشتق‌گیری از دو طرف اتحاد بالا داریم:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\cos \theta ={\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\sin \left(\theta +{\tfrac {\pi }{2}}\right)}$.

استفاده از قاعده زنجیری، با در نظر گرفتن دو تابع به صورت f(θ)=sinθ , g(θ)=θ+π/۲ نتیجه می‌دهد:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}f\!\left(g\!\left(x\right)\right)=f^{\prime }\!\left(g\!\left(x\right)\right)\cdot g^{\prime }\!\left(x\right)=\cos \left(\theta +{\tfrac {\pi }{2}}\right)\cdot (1+0)=\cos \left(\theta +{\tfrac {\pi }{2}}\right)}$.

بازنویسی رابطه بالا، منجر به رابطه زیر می‌شود:

${\displaystyle \cos \left(\theta +{\tfrac {\pi }{2}}\right)=\sin \left(\left(\theta +{\tfrac {\pi }{2}}\right)+{\tfrac {\pi }{2}}\right)=\sin \left(\theta +\pi \right)=-\sin \theta }$.

بنابراین نشان دادیم که

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\cos \theta =-\sin \theta }$.

برای محاسبه مشتق تابع تانژانت، از تعریف مشتق به صورت زیر بهره می‌بریم:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\tan \theta =\lim _{\delta \to 0}\left({\tfrac {\tan(\theta +\delta )-\tan \theta }{\delta }}\right)}$.

با استفاده از اتحاد جمع دو زاویه (tan(α+β) = (tan α + tan β) / (1 - tan α tan β)) داریم:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\tan \theta =\lim _{\delta \to 0}\left[{\frac {{\tfrac {\tan \theta +\tan \delta }{1-\tan \theta \tan \delta }}-\tan \theta }{\delta }}\right]=\lim _{\delta \to 0}\left[{\tfrac {\tan \theta +\tan \delta -\tan \theta +\tan ^{2}\theta \tan \delta }{\delta \left(1-\tan \theta \tan \delta \right)}}\right]}$.

پس از تبدیل حد حاصل‌ضرب به حاصل‌ضرب حدها:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\tan \theta =\lim _{\delta \to 0}{\tfrac {\tan \delta }{\delta }}\times \lim _{\delta \to 0}\left({\tfrac {1+\tan ^{2}\theta }{1-\tan \theta \tan \delta }}\right)}$.

اکنون از حد تابع تانژانت و به صفر میل کردن تانژانت در نزدیکی صفر، بهره می‌بریم:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\tan \theta =1\times {\tfrac {1+\tan ^{2}\theta }{1-0}}=1+\tan ^{2}\theta }$.

رابطه بالا را به صورت زیر نیز می‌توان نوشت:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\tan \theta =1+{\tfrac {\sin ^{2}\theta }{\cos ^{2}\theta }}={\tfrac {\cos ^{2}\theta +\sin ^{2}\theta }{\cos ^{2}\theta }}={\tfrac {1}{\cos ^{2}\theta }}=\sec ^{2}\theta }$.

می‌توان مشتق تابع تانژانت را با قاعده زنجیری نیز به دست آورد:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\tan \theta ={\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}{\tfrac {\sin \theta }{\cos \theta }}={\tfrac {\left(\sin \theta \right)^{\prime }\cdot \cos \theta -\sin \theta \cdot \left(\cos \theta \right)^{\prime }}{\cos ^{2}\theta }}={\tfrac {\cos ^{2}\theta +\sin ^{2}\theta }{\cos ^{2}\theta }}}$.

صورت کسر، بنابر قضیه فیثاغورس، برابر ۱ است. در نتیجه:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\tan \theta ={\tfrac {1}{\cos ^{2}\theta }}=\sec ^{2}\theta }$.

تابع وارون سینوس را به صورت (y=arcsin(x در بازه -π/۲ ≤ y ≤ π/۲ تعریف می‌کنیم؛ بنابراین sin(y)=x. اکنون با استفاده از مشتق ضمنی و حل آن برای dy/dx داریم:

${\displaystyle {d \over dx}\sin y={d \over dx}x}$

${\displaystyle {dy \over dx}\cos y=1}$

با جایگذاری ${\displaystyle \cos y={\sqrt {1-\sin ^{2}y}}}$ و سپس (x=sin(y در معادله بالا:

${\displaystyle {dy \over dx}{\sqrt {1-\sin ^{2}y}}=1}$

${\displaystyle {dy \over dx}{\sqrt {1-x^{2}}}=1}$

${\displaystyle {dy \over dx}={\frac {1}{\sqrt {1-x^{2}}}}}$

تابع وارون کسینوس را به صورت (y=arccos(x در بازه ۰ ≤ y ≤ π تعریف می‌کنیم؛ بنابراین cos(y)=x. اکنون با استفاده از مشتق ضمنی و حل آن برای dy/dx داریم:

${\displaystyle {d \over dx}\cos y={d \over dx}x}$

${\displaystyle -{dy \over dx}\sin y=1}$

با جایگذاری ${\displaystyle \sin y={\sqrt {1-\cos ^{2}y}}}$ و سپس (x=cos(y در معادله بالا:

${\displaystyle -{dy \over dx}{\sqrt {1-\cos ^{2}y}}=1}$

${\displaystyle -{dy \over dx}{\sqrt {1-x^{2}}}=1}$

${\displaystyle {dy \over dx}=-{\frac {1}{\sqrt {1-x^{2}}}}}$

تابع وارون سینوس را به صورت (y=arctan(x در بازه -π/۲ ≤ y ≤ π/۲ تعریف می‌کنیم؛ بنابراین tan(y)=x. اکنون با استفاده از مشتق ضمنی و حل آن برای dy/dx داریم:

${\displaystyle {d \over dx}\tan y={d \over dx}x}$

طرف چپ:

${\displaystyle {d \over dx}\tan y={d \over dx}{\frac {\sin y}{\cos y}}={\frac {{dy \over dx}\cos ^{2}y+\sin ^{2}y{dy \over dx}}{\cos ^{2}y}}={dy \over dx}\left(1+\tan ^{2}y\right)}$

طرف راست:

${\displaystyle {d \over dx}x=1}$

بنابراین

${\displaystyle {dy \over dx}(1+\tan ^{2}y)=1}$

با جایگذاری (x=tan(y در معادله بالا:

${\displaystyle {dy \over dx}(1+x^{2})=1}$

${\displaystyle {dy \over dx}={\frac {1}{1+x^{2}}}}$

تابع وارون سینوس را به صورت (y=arccot(x در بازه -π/۲ ≤ y ≤ π/۲ تعریف می‌کنیم؛ بنابراین cot(y)=x. اکنون با استفاده از مشتق ضمنی و حل آن برای dy/dx داریم:

${\displaystyle {d \over dx}\cot y={d \over dx}x}$

${\displaystyle {dy \over dx}-\csc ^{2}y=1}$

با جایگذاری ${\displaystyle 1+\cot ^{2}y=\csc ^{2}y}$ در معادله بالا:

${\displaystyle {dy \over dx}-(1+\cot ^{2}y)=1}$

با جایگذاری (x=cot(y در معادله بالا:

${\displaystyle {dy \over dx}-(1+x^{2})=1}$

${\displaystyle {dy \over dx}=-{\frac {1}{1+x^{2}}}}$