جدولهای مثلثات
در ریاضیات، جدولهای تابعهای مثلثاتی کاربردهای گوناگونی دارند. پیش از وجود ماشینحساب جیبی، جدولهای مثلثاتی برای ناوبری، علوم و مهندسی ضروری بودند. محاسبهٔ جدولهای ریاضی، موضوع مهمی برای مطالعه بود که منجر به توسعهٔ نخستین دستگاههای محاسب مکانیکی شد.
| مثلثات |
|---|
 |
| منابع |
| قوانین و قضایا |
| حساب دیفرانسیل و انتگرال |
رایانهها و ماشینحسابهای کنونی، با به کار گرفتن کتابخانههای خاص شامل کدهای ریاضی، مقدار توابع مثلثاتی را در لحظه، محاسبه میکنند. این کتابخانهها معمولاً از جدولهای درونی از پیش محاسبهشده بهره میبرند و مقدار مورد نیاز را با درونیابی مییابند. درونیابی با استفاده از جدولهای سادهٔ توابع مثلثاتی هنوز در گرافیک رایانهای که دقت متوسطی لازم است و سرعت محاسبه اهمیت بیشتری دارد، انجام میشود.
یک کاربرد دیگر جدولهای مثلثاتی که اهمیت دارد، در زمینهٔ الگوریتمهای تبدیل فوریهٔ سریع است. در این الگوریتم، در یک تبدیل بارها مقادیر یک تابع مثلثاتی باید محاسبه شوند. در چنین حالتی، فراخوانی چندبارهٔ کتابخانه، سرعت محاسبه را به شدت کاهش میدهد. به جای آن، میتوان کتابخانه را یکبار فراخوانی کرد که جدول مقادیر مثلثاتی مورد نظر را ایجاد کند. این فرایند نیاز به حجم زیادی از حافظه دارد. روش دیگر، بهره گرفتن از رابطهٔ بازگشتی برای محاسبهٔ مثادیر مثلثاتی است.
روابط نصف زاویه و جمع دو زاویه
نخستین روش تهیهٔ جدولهای مثلثاتی از نظر تاریخی و متداولترین روش تا پیش از توسعهٔ رایانهها، اعمال پیاپی اتحادهای نصف زاویه و جمع دو زاویه با آغاز از یک مقدار معلوم (مانند مقادیر زاویهٔ قائمه) بود. نخستین فردی که این اتحادها را در ساخت جدول مثلثاتی به کار برد، بطلمیوس بود. رابطههایی که به این منظور به کار میروند، شامل اتحادهای زیر هستند:
یک روش سریع و نادقیق برای تخمین
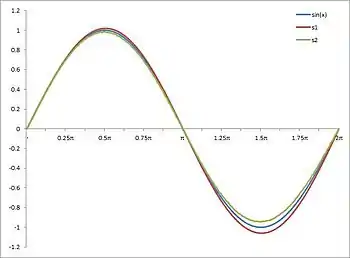
یک الگوریتم تقریبی برای ساختن جدولهای مثلثاتی توابع سسینوس و کسینوس، استفاده پیاپی از رابطههای زیر است:
- s0 = 0
- c0 = 1
- sn+1 = sn + d × cn
- cn+1 = cn − d × sn
که در آنها n عددی صحیح بین صفر و N-۱ است. c و s به ترتیب نشان دهنده کسینوس و سینوس، N تعداد مقدارهای محاسبه شده و d = ۲π/N هستند. این روش تقریبی، بر پایه روش اویلر برای حل معادله دیفرانسیل به صورت انتگرالی:
با شرایط اولیه s(0) = 0 و c(0) = 1 انجام میشود.
این الگوریتم روش مناسبی برای ساختن جدول سینوس نیست. زیرا خطای قابل توجهی دارد که متناسب با ۱N است. برای نمونه، اگر N برابر ۲۵۶ باشد، بیشینه خطای تخمین سینوس حدود ۰٫۰۶۱ و اگر ۱۰۲۴ باشد، بیشینه خطا حدود ۰٫۰۱۵ است.
یک روش بازگشتی دقیقتر
یک رابطه بازگشتی برای تولید جدولهای مثلثاتی بر پایه فرمول اویلر و رابطه
به صورت زیر تعریف میشود:
- c0 = 1
- s0 = 0
- cn+1 = wr cn - wi sn
- sn+1 = wi cn + wr sn
که در آنها n عددی صحیح بین صفر و N-۱ است. همچنین wr=cos۲πN و wi=sin۲πN هستند. این دو مقدار اولیه معمولاً با استفاده از تابعهای کتابخانهای موجود، محاسبه میشوند. با افزایش تعداد جملات، خطا نیز افزایش مییابد.
برای بهبود روش بالا، اصلاحات زیر انجام میشود.
- c0 = 1
- s0 = 0
- cn+1 = cn - (αcn + βsn)
- sn+1 = sn + (βcn - αsn)
که در آن α=sin۲ ۲πN و β=sin۲πN. خطای این روش، بسیار کمتر است. ولی همچنان به اندازهای هست که دقت روشهای سریع مانند تبدیل فوریه سریع را در اندازههای بزرگ، کاهش دهد.
جستارهای وابسته
- تحلیل عددی
- CORDIC
- مقدارهای دقیق مثلثاتی
منابع
- Carl B. Boyer, A History of Mathematics, 2nd ed. (Wiley, New York, 1991).
- Manfred Tasche and Hansmartin Zeuner, "Improved roundoff error analysis for precomputed twiddle factors," J. Computational Analysis and Applications 4 (1), 1–18 (2002).
- James C. Schatzman, "Accuracy of the discrete Fourier transform and the fast Fourier transform," SIAM J. Sci. Comput. 17 (5), 1150–1166 (1996).
- Vitit Kantabutra, "On hardware for computing exponential and trigonometric functions," IEEE Trans. Computers 45 (3), 328–339 (1996).
- R. P. Brent, "Fast Multiple-Precision Evaluation of Elementary Functions", J. ACM 23, 242–251 (1976).
- Singleton, Richard C. (1967). On computing the fast Fourier transform. Comm. ACM, vol. 10, 647–654.
- Gal, Shmuel and Bachelis, Boris. An accurate elementary mathematical library for the IEEE floating point standard, ACM Transaction on Mathematical Software (1991).
