مثلثات تعمیمیافته
مثلثات معمولی، مثلثها را در صفحهٔ دوبعدی مطالعه میکند. در فضای دوبعدی، توابع مثلثاتی با یکی از روشهای تعریف بر پایهٔ مثلث قائمالزاویه، دایرهٔ واحد، سری توانی یا معادلهٔ دیفرانسیل، تعریف میشوند. تعمیم توابع مثلثاتی معمولاً با یکی از روشهای تعریف تابع مثلثاتی آغاز میشود و آن را با فضایی غیر از هندسهٔ اقلیدسی تطابق میدهد. بهطور عام، میتوان مثلثات را علم مطالعهٔ مجموعهای از سه نقطه در هر هندسه یا فضای ممکن دانست. یکی از روشهای تعمیم دادن، مطالعهٔ زاویهها و چندضلعیها در فضای چندبعدی است.
| مثلثات |
|---|
 |
| منابع |
| قوانین و قضایا |
| حساب دیفرانسیل و انتگرال |
مثلثات
- در مثلثات کروی، مثلثهای روی سطح کره مطالعه میشوند. اتحادهای مثلث کروی برحسب توابع مثلثاتی معمولی نوشته میشوند، ولی با اتحادهای مثلث مسطح تفاوت دارند.
- مثلثات هذلولوی:
- مطالعهٔ مثلثهای هذلولوی در هندسهٔ هذلولوی با توابع هذلولوی.
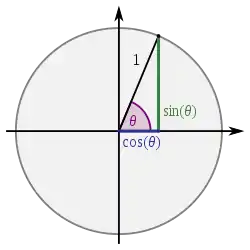
- توابع هذلولوی در هندسهٔ اقلیدسی: پارامترهای دایرهٔ واحد، cost و sint هستند. ولی پارامترهای هذلولی، cosht و sinht هستند.
- مثلثات کسری
- مثلثات در میدان گالوا
- مثلثات فضا-زمان[1]
- مثلثات فازی کیفی[2]
- مثلثات عملگری[3]
چندبعدی
- سینوس قطبی
- قانون سینوسها برای چهاروجهی
توابع مثلثاتی
- توابع مثلثاتی میتوانند برای معادلات دیفرانسیل کسری تعریف شوند.[7]
- تعریف سری سینوس و کسینوس، این تابعها را روی هر فضای جبری که سریها همگرا میشوند، مانند اعداد مختلط و ماتریسها، تعریف میکند.
جستارهای وابسته
منابع
- Herranz, Francisco J.; Ortega, Ramón; Santander, Mariano (2000), "Trigonometry of spacetimes: a new self-dual approach to a curvature/signature (in)dependent trigonometry", Journal of Physics A, 33 (24): 4525–4551, arXiv:math-ph/9910041, doi:10.1088/0305-4470/33/24/309, MR 1768742
- Liu, Honghai; Coghill, George M. (2005), "Fuzzy Qualitative Trigonometry", 2005 IEEE International Conference on Systems, Man and Cybernetics (PDF), 2, pp. 1291–1296, archived from the original (PDF) on 25 July 2011, retrieved 10 April 2015
- Gustafson, K. E. (1999), "A computational trigonometry, and related contributions by Russians Kantorovich, Krein, Kaporin", Вычислительные технологии, 4 (3): 73–83
- Aslaksen, Helmer; Huynh, Hsueh-Ling (1997), "Laws of trigonometry in symmetric spaces", Geometry from the Pacific Rim (Singapore, 1994), Berlin: de Gruyter, pp. 23–36, MR 1468236, CiteSeerX: 10.1.1.160.1580
- Leuzinger, Enrico (1992), "On the trigonometry of symmetric spaces", Commentarii Mathematici Helvetici, 67 (2): 252–286, doi:10.1007/BF02566499, MR 1161284
- Masala, G. (1999), "Regular triangles and isoclinic triangles in the Grassmann manifolds G2(RN)", Rendiconti del Seminario Matematico Università e Politecnico di Torino., 57 (2): 91–104, MR 1974445
- West, Bruce J.; Bologna, Mauro; Grigolini, Paolo (2003), Physics of fractal operators, Institute for Nonlinear Science, New York: Springer-Verlag, p. 101, ISBN 0-387-95554-2, MR 1988873
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
