تاریخ مثلثات
میتوان اثر نخستین مطالعات در زمینه مثلثات را در نوشتههای هزاره دوم پیش از میلاد از جمله ریاضیات مصر باستان و ریاضیات بابل مشاهده کرد. مطالعه مثلثات به عنوان یک علم، در یونان باستان آغاز شد. در همان زمان، ستارهشناسان هندی نیز مثلثات را به کار میگرفتند. به ویژه در دوره گوپتا، افرادی مانند آریابهاتا (سده ششم پیش از میلاد) از توابع مثلثاتی در ستارهشناسی استفاده کردند. در قرون وسطا، مطالعه مثلثات توسط دانشمندان مسلمان ادامه یافت. افرادی چون رگیومونتانوس، مثلثات را به لاتین ترجمه کردند و به اروپا بردند. توسعه مثلثات نوین، در عصر روشنگری توسط دانشمندانی چون آیزاک نیوتن و جیمز استرلینگ آغاز شد و لئونارد اویلر، آن را به شکل امروزی درآورد.
| مثلثات |
|---|
 |
| منابع |
| قوانین و قضایا |
| حساب دیفرانسیل و انتگرال |
نامگذاری
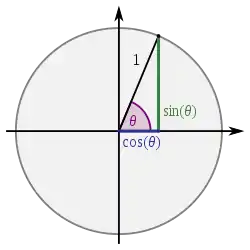
نامگذاری مثلثات در علوم اسلامی، به دلیل آن است که پایه این علم، مثلث است. نام سینوس از واژه سانسکریت جیوا گرفته شدهاست. این واژه در عربی، به جیب تبدیل شد و پس از ترجمه متون عربی به لاتین، مترجمان که آن را به اشتباه، جَیب (به معنی خلیج) خوانده بودند، این واژه را به سینوس (به معنی خلیج) برگرداندند.[1]
توسعه
مثلثات اولیه
ریاضیات مصر باستان و ریاضیات بابل، قضیههایی را در زمینه نسبت میان اضلاع مثلثهای مشابه میدانستند. البته از آنجایی که جامعههای پیش از یونان باستان، مفهوم اندازهگیری زاویه را نمیدانستند، به جای آن، محدود به مطالعه اضلاع مثلث بودند.[2]
ستارهشناسان بابلی، جزئیات اندازهگیری طلوع و غروب ستارهها، حرکت سیارات و کسوف و خسوف را ثبت میکردند. برای همه این موارد، آشنایی با اندازهگیری زاویهها ضروری بود.[3] برخی معتقدند که بابلیان جدول سکانتها را هم تهیه کرده بودند.[4] البته مشخص نیست که این جدول، مربوط به مثلثهای فیثاغورسی، حل معادلات درجه دوم یا جدول مثلثاتی بودهاست.
از سوی دیگر، مصریان شکل اولیهای از مثلثات را برای ساختن اهرام در هزاره دوم پیش از میلاد به کار میبردند.[3]
ریاضیات یونان
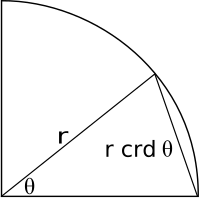
ریاضیدانان یونان باستان، از وتر استفاده میکردند. وتر، پارهخطی در دایره و روبروی یک زاویه مرکزی است که دو نقطه روی محیط دایره را به یکدیگر وصل میکند. عمود منصف وتر، از مرکز دایره میگذرد. نصف وتر، برابر سینوس نصف زاویه مرکزی روبروی آن است. به زبان ریاضی:
و در نتیجه، تابع سینوس به عنوان نصف وتر، شناخته میشود. به دلیل این رابطه، تعدادی از اتحادهای مثلثاتی کنونی برای ریاضیدانان یونان باستان، البته در شکل وتر معادل آنها، شناخته شده بودند.[5]
هرچند که مثلثات در کارهای اقلیدس و ارشمیدس به وضوح دیده نمیشود، ولی برخی از قضیههای آنان به روشی هندسی (به جای مثلثاتی) ارائه شدهاند که معادل با برخی قانونها یا فرمولهای مثلثاتی هستند.[2] برای نمونه، گزارههای ۱۲ و ۱۳ کتاب دوم عناصر، قانون کسینوسها به ترتیب برای زاویههای باز و تند هستند. قضیههایی در مورد وتر، کاربرد قانون سینوسها میباشند. قضیه ارشمیدس در وترهای شکسته، معادل رابطههای سینوس جمع و تفاضل دو زاویه است.[2] برای جبران نبود جدول وترها، ریاضیدانان عصر آریستارخوس گاهی از رابطهای که شکل نوین آن به صورت sinαsinβ<αβ<tanαtanβ برای زاویههایی در بازه ۰°<β<α<۹۰° با نام نابرابری آرسیستارخوس شناخته میشود، استفاده میکردند.[6]
ظاهراً نخستین جدول مثلثاتی توسط ابرخس نیقیه (۱۸۰ - ۱۲۵ پ.م) ایجاد شده و او به همین دلیل، اکنون با نام پدر مثلثات شناخته میشود.[7] ابرخس نخستین کسی بود که مقدار کمان و وتر متناظر با مجموعهای از زاویهها را جدولبندی کرد.[7]
هرچند که زمان آغاز استفاده از دایره °۳۶۰ در ریاضیات مشخص نیست، ولی میدانیم که دایره °۳۶۰ مدت کوتاهی پس از آن که آریستارخوس ساموسی مقاله در اندازهها و فاصلههای خورشید و ماه را نوشت، به ریاضیات معرفی شد. زیرا او زاویه را برحسب نسبتی از ربع دایره، اندازهگیری کرد.[6] به نظر میرسد که استفاده عملی از دایره °۳۶۰ بسیار تحت تأثیر جدول وترهای ابرخس بودهاست. ممکن است که ابرخس ایده این تقسیمبندی را از هیپسیکلس که پیشتر روز را به ۳۶۰ بخش، تقسیم کردهبود گرفته باشد. این تقسیمبندی روز احتمالاً توسط ستارهشناسان بابلی پیشنهاد شدهاست.[8]
منلائوس اسکندریه سه کتاب اسفریکا را نوشت. در نخستین کتاب، بر پایه مثلثات صفحهای اقلیدس، پایهای برای مثلثات کروی قرار داد.[5] او قضیهای را که متناظر اقلیدسی ندارد، به این صورت برقرار نمود که دو مثلث کروی متجانس هستند، اگر زاویههای متناظر آنها برابر باشند. ولی او بین مثلثهای کروی متجانس و متقارن، تفاوتی قائل نشد.[5] قضیه دیگر او، این است که جمع زاویههای یک مثلث کروی، از °۱۸۰ درجه بیشتر است.[5] کتاب دوم اسفریکا هندسه کروی را در ستارهشناسی اعمال میکند و کتاب سوم، شامل قضیه منلائوس است.[5] او بعدتر قانون مشهور شش مقدار را ارائه کرد.[9]
مدتی پس از منلائوس، کلودیوس بطلمیوس وترهای دایرهای ابرخس را در کتاب المجسطی خود توسعه داد. المجسطی در اصل، کاری در زمینه ستارهشناسی است و ستارهشناسی وابسته به مثلثات میباشد. جدول وترهای بطلمیوس، اندازه وترهای یک دایره با قطر ۱۲۰ را به عناون تابعی از درجه در کمان متناظر در بازه ۱/۲ تا ۱۸۰ با گام ۱/۲ میدهد.[10] ۱۳ کتاب المجسطی تأثیرگذارترین و مهمترین کار مثلثاتی دوران باستان است.[11] یک قضیه که اساس محاسبات وتری بطلمیوس بود، قضیه بطلمیوس است. بر پایه این قضیه، مجموع حاصلضرب ضلعهای روبرو در یک چهارضلعی محاطی برابر با حاصلضرب دو قطر آن است. یک حالت خاص قضیه بطلمیوس، در گزاره ۹۳ کتاب داتای اقلیدس مشاهده میشود. قضیه بطلمیوس منجر به چهار رابطه جمع و تفاضل سینوس و کسینوس شد که اکنون با نام فرمولهای بطلمیوس شناخته میشوند. هرچند که خود بطلمیوس، به جای سینوس و کسینوس از وتر استفاده کرد.[11] بطلمیوس بعدتر رابطه نصف زاویه را نیز استخراج نمود.
بطلمیوس از این نتایج برای ساخت جدولهای مثلثاتی حود بهره گرفت. ولی این که آیا این جدولها از کار ابرخس گرفته شدهاند، مشخص نیست.[11]
اکنون اثری از هیچ یک از جدولهای ابرخس و بطلمیوس وجود ندارد. ولی توصیفات سایر نویسندگان باستان، احتمال وجود آنها را افزایش میدهد.[12]
ریاضیات هند
برخی از توسعههای اولیه و بسیار مهم مثلثات در هند، انجام شد. کارهای تأثیرگذاری در سدههای ۴ و ۵ میلادی که با نام سیدهانتا (شامل ۵ کتاب که یکی از آنها با نام سوریا سیدهانتا بیش از بقیه باقی مانده) شناخته میشوند،[13]) برای نخستین بار، سینوس را به صورت نوین آن (به شکل رابطه میان نصف زاویه و نصف وتر) و نیز کسینوس را تعریف نمودند.[14] پس از مدتی کوتاه، آریابهاتا سیدهانتاها را در کتابی به نام آریابهاتیا جمعآوری کرد و آن را توسعه داد.[15] سیدهانتاها و آریابهاتیا شامل نخستین جدولهای بازمانده مقدارهای سینوس در بازه ۰ تا ۹۰ درجه با گام ۳٫۷۵ درجه و با دقت ۴ رقم اعشارهستند.[16] آنان از واژه جیا برای سینوس و کوجیا برای کسینوس استفاده میکردند.
در سده هفتم میلادی، باسکارای اول رابطهای برای محاسبه سینوس یک زاویه تند بدون استفاده از جدول، ایجاد کرد. او همچنین رابطه تقریبی زیر را برای سینوس ارائه کرد که دارای خطای نسبی کمتر از ۱٫۹٪ است:
مدتی بعد براهماگوپتا رابطه را اصلاح کرد:[17]
باسکارای دوم، یک محقق هندی دیگر بود که در سده دوازدهم میلادی مثلثات کروی را توسعه داد و بسیاری از نتایج مثلثاتی را کشف نمود. باسکارای دوم نخستین کسی بود که رابطههای جمع و تفاضل دو زاویه مانند رابطههای زیر را کشف کرد:
مدهاوا (سده ۱۴ میلادی) نخستین تحلیلهای ریاضی تابعهای مثلثاتی و بسطهای نامتناهی آنها را انجام داد. او مفهوم سری توانی و سری تیلور را ایجاد کرد و بسط سری توانی سینوس، کسینوس، تانژانت و آرکتانژانت را تهیه کرد.[18][19] با استفاده از تقریب سری تیلور سینوس و کسینوس، او جدول سینوس را تا ۱۲ رقم اعشار و جدول کسینوس را تا ۹ رقم اعشار تهیه کرد. او سری توانی عدد π، شعاع، قطر و محیط یک دایره را برحسب تابعهای مثلثاتی ارائه داد. شاگردانش در مدرسه ستارهشناسی و ریاضیات کرالا کارهای او را تا سده ۱۶ میلادی ادامه دادند.[18][19]
| ردیف | سری | نام | کاشفان غربی سریها و تاریخ تقریبی کشف[20] |
|---|---|---|---|
| ۱ | sin x = x - x33! + x55! - x77! + ... | سری سینوس مدهاوا | آیزاک نیوتون (۱۶۷۰) و ویلهلم لایبنیتز (۱۶۷۶) |
| ۲ | cos x = 1 - x22! + x44! - x66! + ... | سری کسینوس مدهاوا | آیزاک نیوتون (۱۶۷۰) و ویلهلم لایبنیتز (۱۶۷۶) |
| ۳ | tan-۱x = x - x33 + x55 - x77 + ... | سری آرکتانژانت مدهاوا | جیمز گرگوری (۱۶۷۱) و ویلهلم لایبنیتز (۱۶۷۶) |
نوشته هندی یوکتیبهاسا شامل اثبات بسط تابعهای سینوس و کسینوس و استخراج و اثبات سری توانی برای وارون تانژانت است که توسط مدهاوا کشف شدند. این نوشته، شامل قانونهایی برای یافتن سینوس و کسینوس جمع و تفاضل دو زاویه نیز هست.
دوران اسلامی
.png.webp)
کارهای هندیان، در عصر طلایی اسلام، توسط ریاضیدانان مسلمان فارسیزبان و عربزبان ترجمه شدند و گسترش یافتند. آنان مثلثات زا از وابستگی ربع دایره (در ریاضیات یونانی به دلیل قضیه منلائوس) خارج کردند. پس از این توسعه در ریاضیات اسلامی، مثلثات به صورت علمی مجزا که به مطالعه مثلثهای مسطح و کروی و اضلاع و زاویههای آنها میپردازد، معرفی شد.[21]
افزون بر کارهای هندیان، مسلمانان با روشهای یونانی برای استفاده از مثلثهای کروی، به ویژه روش منلائوس که قضیه منلائوس را برای حل مسائل کروی توسعه داد، آشنا بودند.[5][22] برای تعیین روزهای مقدس در تقویم اسلامی که زمانبندی آن بر پایه گردش ماه بود، ستارهشناسان نخست از روش منلائوس برای محاسبه موقعیت ماه و ستارهها استفاده میکردند. در این روش، دو مثلث قائمالزاویه متقاطع در نظر گرفته میشدند و با اعمال قضیه منلائوس با معلوم بودن پنج ضلع، اندازه ضلع ششم به دست میآمد. معلوم شد که این روش، مشکل است. برای برخی محاسبات مانند تعیین زمان از روی ارتفاع خورشید، تکرار چندباره قضیه منلائوس ضروری بود. به همین دلیل، ریاضی دانان مسلمان بر آن شدند که روش مثلثاتی تازهای پیدا کنند.[23]
در سده نهم میلادی، محمد ابن موسی خوارزمی جداول دقیق سینوس و کسینوس و نخستین جدول تانژانت را تهیه کرد. او سهم زیادی نیز در توسعه مثلثات کروی دارد. در ۸۳۰ میلادی، مروزی نخستین جدول کتانژانت را تهیه کرد.[24][25] بتانی تابعهای معکوس سکانت و کسکانت را کشف کرد و نخستین جدول کسکانت را برای هر درجه از °۱ تا °۹۰ تهیه کرد.[25]
در سده دهم میلادی، هر شش تابع مثلثاتی در کار ابوالوفا بوزجانی مورد استفاده قرار میگرفتند.[26] ابوالوفا جدولهای سینوس را با گام °۰٫۲۵ با دقت ۸ رقم اعشار و جدولهای دقیق تانژانت را در اختیار داشت.[26] او رابطه مثلثاتی زیر را نیز ایجاد نمود:[27]
ابوالوفا اتحادهای جمع و تفاضل دو زاویه را نیز با اثبات کاملشان ارائه داد:[27]
او قانون سینوسها را برای مثلثات کروی نیز کشف کرد:[24]
در اواخر سده دهم و اوایل سده یازدهم میلادی، ابن یونس (ستارهشناس مصری) محاسبات مثلثاتی دقیق را انجام داد و اتحاد مثلثاتی زیر را به دست آورد:[28]
جیانی در سده یازدهم در آندلس کتاب کمانهای مجهول کره را نوشت که شامل نخستین برخوردها با مثلثات کروی در شکل نوین آن است.[29] این کتاب شامل رابطههایی برای مثلثهای قائمالزاویه کروی، قانون عمومی سینوسها و حل یک مثلث کروی با استفاده از مثلثهای قطبی است. این نحوه برخورد او بعداً تأثیر بزرگی در ریاضیات اروپا داشت و به نظر میرسد تعریف نسبتها با اعداد و روش حل مثلث کروی هنگامی که همه اضلاع مجهول هستند توسط جیانی تأثیراتی داشتهاند.[29]
ریاضیدانان مسلمان، روش مثلثسازی را ایحاد کردند و از آن در کارهای عملی مانند نقشهبرداری[30] و جغرافیا (که در آغاز سده یازدهم میلادی توسط ابوریحان بیرونی شرح داده شده) استفاده نمودند. بیرونی شیوههای مثلثسازی برای اندازهگیری ابعاد زمین و فاصله میان مکانهای مختلف را معرفی کرد.[31] در پایان سده یازدهم، عمر خیام معادلات درجه سوم را با حل عددی تقریبی که از درونیابی جداول مثلثاتی به دست میآمد، حل کرد. خواجه نصیرالدین طوسی در سده سیزدهم، نخستین کسی بود که مثلثات را به عنوان یک شاخه ریاضیات و مستقل از ستارهشناسی در نظر گرفت و مثلثات کروی را به شکل امروزی آن درآورد.[25] او فهرستی از شش حالت مثلث قائمالزاویه در مثلثات کروی تهیه کرد و قانون سینوسها را برای مثلثهای مسطح و کروی بیان نمود، قانون تانژانتها را برای مثلثهای کروی کشف کرد و اثباتهایی برای این دو قانون ارائه کرد.[32]
در سده پانزدهم، غیاثالدین جمشید کاشانی نخستین تعریف صریح قانون کسینوسها را به صورتی که برای مثلثسازی مناسب باشد، بیان کرد. او سینوس زاویه °۱ را نیز با حل معادله درجه ۳ برحسب زاویه °۳ تا ۱۷ رقم اعشار محاسبه کرد.[33]
ریاضیات چین

در چین، کتاب آریابهاتا در ۷۱۸ میلادی در دوره سلسله تانگ، ترجمه شد.[34] هرچند که چینیان در زمینههای دیگر ریاضی مانند قضیه دوجملهای، فرمولهای جبری مختلط و هندسه فضایی تبحر داشتند، نخستین شکلهای مثلثات به اندازه یونان بوستان، هند و جهان اسلام، در چین مورد استفاده قرار نداشت.[35] به جای آن، چینیان از یک روش تجربی جایگزین استفاده میکردند و استفاده عملی از سینوس، تانژانت و سکانت در هندسه مسطحه، شناختهشده بود.[34] البته این شکل ابتدایی مثلثات به تدریج در دوره سلسله سونگ تغییر یافت و پیشرفت کرد و ریاضیدانان چینی توجه بیشتری به مثلثات کروی مبذول کردند. زیرا برای محاسبات تقویمی و ستارهشناسی به این علم نیاز داشتند.[34]
شن کو، دانشمند و ریاضیدان چینی سده یازدهم، از توابع مثلثاتی برای حل مسائل مربوط به کمانها و وترها استفاده کرد.[34] شن کو یک رابطه تقریبی برای محاسبه طول کمان s در دایرهای به قطر d، زه (فاصله مرکز کمان تا مرکز وتر متناظر آن) v و طول وتر متناظر c به دست آورد:[36]
گو شوجینگ در سده سیزدهم، از کارهای شن کو در اندازهگیری کمان برای توسعه مثلثات کروی بهره برد.[37] گو در محاسبات خود برای بهبود تقویم چینی و ستارهشناسی چینی از مثلثات کروی استفاده کرد.[34][38] با وجود دستاوردهای شن و گو در مثلثات، تا سال ۱۶۰۷، هیچ کار بنیادی دیگری در چین در این زمینه انجام نشد. در این سال، عناصر اقلیدسی توسط شو گانگکی منتشر شد.[39]
ریاضیات اروپا

لوی بن گرشون در ۱۳۴۲ در سینوسها، وترها و کمانها را نوشت که موضوع اصلی آن، اثبات قانون سینوسها برای مثلثهای مسطح بود.[40] یک جدول مثلثاتی سادهشده در سدههای ۱۴ و ۱۵ میلادی توسط ملوانان در دریای مدیترانه برای محاسبه دورههای ناوبری مورد استفاده قرار میگرفت. احتمالاً رگیومونتانوس نخستین فرد اروپایی بود که مثلثات را به عنوان یک شاخه مستقل ریاضیات مورد مطالعه قرار داد.[41] رتیکوس که شاگرد کوپرنیک بود، احتمالاً نخستین فرد اروپایی بود که تابعهای مثلثاتی را به جای دایره، مستقیماً بر پایه مثلث قائمالزاویه تعریف کرد. او جدولهایی را نیز برای شش تابع مثلثاتی ارائه داد. والنتین اوتو که شاگرد رتیکوس بود، این کار را تکمیل کرد.
در سده هفدهم میلادی، آیزاک نیوتن و جیمز استرلینگ فرمول درونیابی عمومی نیوتن-استرلینگ را برای تابعهای مثلثاتی ایجاد کردند.
در سده هجدهم لئونارد اویلر روش برخورد تحلیلی با تابع مثلثاتی را بنا نهاد، سری نامتناهی آنها را به دست آورد و فرمول اویلر (eix=cosx+isinx) را ارائه کرد. پیش از او، روژه کوته مشتق سینوس را محاسبه کردهبود.[42] همچنین در سده هجدهم، بروک تیلور سری عمومی تیلور را تعریف کرد و بسط تیلور و تقریبهای هر شش تابع مثلثاتی را ارائه کرد.
جستارهای وابسته
پانویس
- Boyer (1991), page 252
- Boyer (1991). "Greek Trigonometry and Mensuration". pp. 158–159. Missing or empty
|title=(help) - Maor, Eli (1998). Trigonometric Delights. Princeton University Press. p. 20. ISBN 0-691-09541-8.
- Joseph (2000b, pp.383–84).
- Boyer (1991). "Greek Trigonometry and Mensuration". p. 163. Missing or empty
|title=(help) - Boyer (1991). "Greek Trigonometry and Mensuration". p. 159. Missing or empty
|title=(help) - Boyer (1991). "Greek Trigonometry and Mensuration". p. 162. Missing or empty
|title=(help) - Boyer (1991). "Greek Trigonometry and Mensuration". p. 162. Missing or empty
|title=(help) - Needham, Volume 3, 108.
- Toomer, G. J. (1998), Ptolemy's Almagest, Princeton University Press, ISBN 0-691-00260-6
- Boyer (1991). "Greek Trigonometry and Mensuration". pp. 164–166. Missing or empty
|title=(help) - Boyer, pp. 158-168.
- Boyer (1991), p. 208.
- Boyer (1991), p. 209.
- Boyer (1991), p. 210
- Boyer (1991), p. 215
- Joseph (2000a, pp.285-86).
- O'Connor and Robertson (2000).
- Pearce (2002).
- Charles Henry Edwards (1994). The historical development of the calculus. Springer Study Edition Series (3 ed.). Springer. p. 205. ISBN 978-0-387-94313-8.
- Kennedy, E. S. (1969). "The History of Trigonometry". 31st Yearbook. National Council of Teachers of Mathematics, Washington DC. (cf. Haq, Syed Nomanul. "The Indian and Persian background": 60–3., in Seyyed Hossein Nasr, Oliver Leaman (1996). History of Islamic Philosophy. Routledge. pp. 52–70. ISBN 0-415-13159-6.)
- O'Connor, John J.; Robertson, Edmund F., "Menelaus of Alexandria", بایگانی تاریخچه ریاضیات مکتیوتر, دانشگاه سنت اندروز. "Book 3 deals with spherical trigonometry and includes Menelaus's theorem."
- Gingerich, Owen (April 1986). "Islamic astronomy". Scientific American. 254 (10): 74. doi:10.1038/scientificamerican0486-74. Archived from the original on 19 October 2013. Retrieved 2008-05-18.
- Jacques Sesiano, "Islamic mathematics", p. 157, in Selin, Helaine; D'Ambrosio, Ubiratan, eds. (2000). Mathematics Across Cultures: The History of Non-western Mathematics. Springer. ISBN 1-4020-0260-2.
- "trigonometry". Encyclopædia Britannica. Retrieved 2008-07-21.
- Boyer (1991) p. 238.
- Moussa, Ali (2011). "Mathematical Methods in Abū al-Wafāʾ's Almagest and the Qibla Determinations". Arabic Sciences and Philosophy. Cambridge University Press. 21 (1): 1–56. doi:10.1017/S095742391000007X.
- William Charles Brice, 'An Historical atlas of Islam', p.413
- O'Connor, John J.; Robertson, Edmund F., "Abu Abd Allah Muhammad ibn Muadh Al-Jayyani", بایگانی تاریخچه ریاضیات مکتیوتر, دانشگاه سنت اندروز.
- Donald Routledge Hill (1996), "Engineering", in Roshdi Rashed, Encyclopedia of the History of Arabic Science, Vol. 3, p. 751–795 [769].
- O'Connor, John J.; Robertson, Edmund F., "Abu Arrayhan Muhammad ibn Ahmad al-Biruni", بایگانی تاریخچه ریاضیات مکتیوتر, دانشگاه سنت اندروز.
- Berggren, J. Lennart (2007). "Mathematics in Medieval Islam". The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. p. 518. ISBN 978-0-691-11485-9.
- قربانی، زندگینامهٔ ریاضیدانان دورهٔ اسلامی از سدهٔ سوم تا سدهٔ یازدهم هجری، ۳۶۸.
- Needham, Volume 3, 109.
- Needham, Volume 3, 108–109.
- Katz, 308.
- Restivo, 32.
- Gauchet, 151.
- Needham, Volume 3, 110.
- Simonson, Shai. "The Mathematics of Levi ben Gershon, the Ralbag" (PDF). Retrieved 2009-06-22.
- Boyer, p. 274
- "The calculus of the trigonometric functions", Historia Mathematica Volume 14, Issue 4, November 1987, Pages 311–324, by Victor J. Katz doi 10.1016/0315-0860(87)90064-4, the proof of Cotes is mentioned on p. 315.
منابع
{سایت:ویکی پدیا}* استرویک، درک (۱۳۶۶). تاریخ فشرده ریاضیات. ترجمهٔ غلامرضا برادران خسروشاهی، حشمتالله کامرانی. نشر نو.