مثلثات
مثلثات یا سهبَرسنجی[1] (به انگلیسی: Trigonometry) یکی از شاخههای ریاضیات است که روابط میان طول اضلاع و زاویههای مثلث را مطالعه میکند. نخستین کاربرد مثلثات در مطالعات اخترشناسی بودهاست. اکنون مثلثات کاربردهای زیادی در ریاضیات محض و کاربردی دارد.
| مثلثات |
|---|
 |
| منابع |
| قوانین و قضایا |
| حساب دیفرانسیل و انتگرال |
بعضی از روشهای بنیادی تحلیل، مانند تبدیل فوریه و معادلات موج، از توابع مثلثاتی برای توصیف رفتار تناوبی موجود در بسیاری از فرایندهای فیزیکی استفاده میکنند. همچنین مثلثات پایه علم نقشهبرداری است.
سادهترین کاربرد مثلثات در مثلث قائمالزاویه است. هر شکل هندسی دیگری را نیز میتوان به مجموعهای از مثلثهای قائمالزاویه تبدیل کرد. شکل خاصی از مثلثات، مثلثات کروی است که برای مطالعه مثلثات روی سطوح کروی و منحنی به کار میرود.
تاریخچه
احتمالاً مثلثات برای استفاده در ستارهشناسی ایجاد شده و کاربردهای اولیه آن نیز در همین باره بودهاست. خواجه نصیرالدین طوسی دانشمند ایرانی پدر علم مثلثات بعنوان شاخه ای از ریاضیات که بصورت امروزی بکار می رود شناخته می شود
واژگان مثلثات در متون فارسی و عربی قدیم با امروزه تفاوت داشت. برخی از این تفاوتها از این قرار است:[2]
| نام قدیم در فارسی | معنی نام | نام امروزی |
|---|---|---|
| جیب | گریبان | سینوس |
| جیب تمام | گریبان پُر | کسینوس |
| ظل، ظل معکوس | سایه | تانژانت |
| ظل تمام، ظل مستوی | سایه پُر | کتانژانت |
| قاطع، قطر ظل | بُرنده | سکانت |
| قاطع تمام | بُرنده پُر | کسکانت |
کلیات
تابعهای اصلی مثلثات
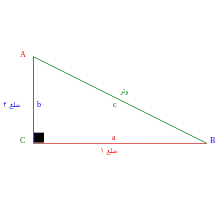
مجموع زاویههای داخلی مثلث برابر ۱۸۰ درجه است؛ بنابراین در مثلث قائمالزاویه با داشتن مقدار یک زاویه تند، میتوان مقدار زاویه دیگر را به دست آورد. با مشخص بودن زاویهها میتوان نسبت میان اضلاع را یافت. به این ترتیب، اگر اندازه یک ضلع معلوم باشد، اندازه دو ضلع دیگر قابل محاسبه است. نسبت میان اضلاع مثلث، با استفاده از توابع مثلثاتی زیر، محاسبه میشود. در شکل روبرو، برای زاویه تند A که مجاور وتر c و ضلع b و روبرو به ضلع a است، داریم:
- تابع سینوس که به صورت نسبت ضلع مقابل به وتر تعریف میشود:
- تابع کسینوس که به صورت نسبت ضلع مجاور به وتر تعریف میشود:
- تابع تانژانت که به صورت نسبت ضلع مقابل به ضلع مجاور تعریف میشود:
توابع مثلثاتی برای زاویه B نیز به همین ترتیب قابل محاسبه هستند. از آنجایی که ضلع مقابل زاویه A مجاور زاویه B است و برعکس، سینوس یک زاویه برابر با کسینوس زاویه دیگر است. به عبارت دیگر: و .
عکس تابعهای بالا نیز با نامهای سکانت (معکوس کسینوس)، کسکانت (معکوس سینوس) و کتانژانت (معکوس تانژانت) تعریف میشوند.
| سکانت: | |
| کسکانت: | |
| کتانژانت: |
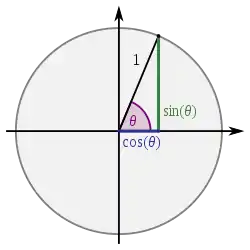
دایره واحد مثلثاتی

تابعهای مثلثاتی برای زاویههای تند بر اساس رابطههای بالا محاسبه میشوند. برای زاویههای بزرگتر از ۹۰ درجه (π/۲ رادیان)، میتوان از مفهوم دایره مثلثاتی بهره گرفت. در دایره مثلثاتی، هر زاویهای از صفر تا ۳۶۰ درجه را میتوان رسم کرد و تابعهای مثلثاتی آن را به دست آورد. همان گونه که در شکل روبرو دیده میشود، تابعهای مثلثاتی برای زاویههای بزرگتر از ۹۰ درجه را میتوان به صورت تابعی از زاویههای کوچکتر از ۹۰ درجه، یافت. برای نمونه، تابعهای مثلثاتی برای زاویههای ربع دوم دایره (۹۰ تا ۱۸۰ درجه) با دوران دایره مثلثاتی به میزان ۹۰ درجه، به صورت جدول زیر به دست میآیند:
| دوران π/۲ |
|---|
تناوب
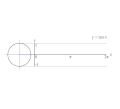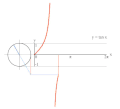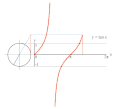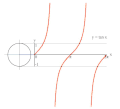
تابعهای مثلثاتی برای زاویههای بزرگتر از ۳۶۰ درجه (۲π) و کوچکتر از صفر درجه نیز تعریف میشوند. برای هر زاویه 'θ مقدار تابع، برابر با مقدار تابع برای زاویه θ درون دایره (۰<θ<۳۶۰) خواهد بود که در رابطه θ'=۳۶۰+۲kθ صدق کند؛ بنابراین تابعهای مثلثاتی با یک تناوب مشخص تکرار میشوند. دوره تناوب تابعهای تانژانت و کتانژانت، ۱۸۰ درجه (π) و دوره تناوب سایر تابعها ۳۶۰ درجه (۲π) است.
تابع وارون
برای تابعهای مثلثاتی، تابع وارون در بازه مشخصی که شرط یک به یک بودن تابع برقرار باشد، تعریف میشود. این تابعها متناظر با تابع اصلی، آرکسینوس، آرککسینوس و آرکتانژانت نامیده میشوند.
زاویههای مرزی
| ربع | زاویه + | زاویه - |
|---|---|---|
| ربع اول | ||
| ربع دوم | ||
| ربع سوم | ||
| ربع چهارم |
یاد آور علامت توابع مثلثاتی در هر ناحیه دایره مثلثاتی
- در ربع اول همه نسبتهای مثلثاتی مثبت هستند.
- در ربع دوم سینوسها مثبت هستند.
- در ربع سوم تانژانت مثبت هستند.
- در ربع چهارم کسینوسها مثبت هستند.
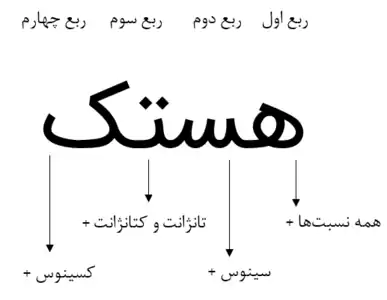
نکته: برای فهمیدن نکته بالا راهکار سادهای وجود دارد.
با توجه به این مطلب که هستک اتم به دلیل وجود پروتون بار الکتریکی مثبت دارد :
- ه: همه نسبتهای مثلثاتی در ربع اول مثبت است.
- س: سینوس در ربع دوم مثبت است.
- ت: تانژانت در ربع سوم مثبت است.
- ک: کسینوس در ربع چهارم مثبت است.
جدول تعیین علامت
| نسبتهای مثلثاتی | ربع اول | ربع دوم | ربع سوم | ربع چهارم |
|---|---|---|---|---|
روابط اصلی
بعضی از رابطههای مثلثاتی برای همه زاویهها بر قرار هستند که به این رابطهها، اتحاد مثلثاتی گفته میشود. از جمله، برخی از این اتحادها در تعیین مشخصات مثلث (مانند مساحت و شعاع دایره محیطی) کاربرد دارند و برخی برای محاسبه تابعهای مثلثاتی برای مجموع یا تفاضل دو زاویه مورد استفاده قرار میگیرند.
اتحادهای فیثاغورس
اتحاد اصلی به صورت زیر است:
میتوان از اتحاد بالا دو اتحاد دیگر را استخراج نمود:
قانون سینوسها
با استفاده از قانون سینوسها در هر مثلث دلخواه، میتوان با معلوم بودن اندازه یک ضلع و دو زاویه مجاور آن، اندازه دو ضلع دیگر را محاسبه نمود. همچنین میتوان مساحت مثلث (Δ) و شعاع دایره محیطی آن (R) را به دست آورد:
بر اساس اتحاد بالا، مساحت مثلث با معلوم بودن اندازه دو ضلع و زاویه میان آنها از رابطه زیر، قابل محاسبه است:
قانون کسینوسها
با استفاده از قانون کسینوسها در هر مثلث دلخواه، با معلوم بودن اندازه دو ضلع و زاویه میان آنها، اندازه ضلع سوم به صورت زیر تعیین میشود:
رابطههای تبدیل زاویه
برخی روابط مثلثاتی
نگارخانه
پانوشته
دایره مثلثاتی یا دایره واحد «سیده فاطمه موسوی نطنزی»
جستارهای وابسته
منابع
- احمد فیروزنیا (۱۳۸۲)، مثلثات، تهران: انتشارات مدرسه، شابک ۹۶۴-۳۸۵-۰۱۴-۵
- واژهنامهٔ ریشهشناختی اخترفیزیک، دکتر حیدری ملایری
- نیر نوری (۱۳۷۵–۱۳۷۷). سهم ارزشمند ایران در فرهنگ جهان. تهران: انجمن آثار و مفاخر فرهنگی. صص. ۲۴۰. شابک ۹۶۴۶۲۷۸۲۰۵.