تابع علامت
در ریاضیات، تابع علامت تابعی فرد است که علامت یک عدد حقیقی را بدست میدهد. در ریاضی با نماد sgn کاربرد دارد که کوتاهنوشتی برای sign به معنی علامت است، چرا که، اعداد را بر حسب علامتشان جدا میکند. این تابع نمونهای از توابع چند ضابطهای است.
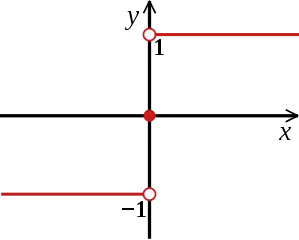
ویژگیها
هر عدد حقیقی را میتوان به صورت حاصل ضرب قدر مطلق آن در تابع علامتش نوشت:
از معادلهٔ بالا چنین بدست میآید که هرگاه x ناصفر باشد تابع علامت آن را میتوان به صورت زیر بازنویسی کرد:
و البته برای تمامی اعداد حقیقی x میتوان گفت:
تابع علامت مشتق تابع قدر مطلق نیز است (تا سر نامعینی در صفر):
آنچه باقی میماند تنها علامت x است.
تابع علامت در همه جا جز صفر، مشتقپذیر است و مقدار مشتق آن برابر صفر است. این تابع در حالت عادی در نقطهٔ صفر مشتقپذیر نیست ولی در شرایط مفهوم عمومی مشتقگیری در نظریهٔ توزیع، مشتق تابع علامت برابر است با دو برابر تابع دلتای دیراک که برای بیان آن میتوان از رابطهٔ زیر بهره برد:[1]
که در آن H(x) تابع پلهای هویساید است و H(۰) = ۱/۲ میباشد. با کمک این برابری دوباره مشتقگیری میکنیم:[2]
می توان تابع علامت را به کمک براکت ایورسون هم نوشت:
که در آن ، تقریب مناسبی برای تابع علامت به صورت زیر است:
تقریب دیگر چنین است:
که برای مقدار آن نزدیکتر به دقیق میشود. یادآوری میشود که این رابطه مشتق است. این مطلب از آنجا بدست آمده که: رابطهٔ بالا در صورت صفر بودن برای تمام xهای ناصفر رابطهای دقیق است و مانند تعمیم دادن تابع علامت در بُعدهای دیگر میماند (مانند مشتق جزئی ).
نگاه کنید به مقالهٔ تابع پلهای هویساید.
تابع علامت مختلط
تابع علامت را میتوان تا مجموعهٔ اعداد مختلط هم گسترش داد؛ به این ترتیب:
که در آن z عضو است مگر در نقطهٔ صفر. تابع علامت عدد دلخواه z در مجموعهٔ اعداد مختلط، برابر با نقطهای است روی دایره واحد یک صفحهٔ مختلط که در نزدیکترین فاصله به z قرار دارد. پس برای zهای ناصفر داریم:
در این رابطه arg همان زاویهٔ φ در بیان قطبی عدد مختلط است. توضیح: اگر یک عدد مختلط را به صورت یا نمایش دهیم، arg همان زاویهٔ φ است. به دلیل تقارن و همچنین برای آنکه تابع را به تمامی تعمیم داده باشیم، برای نقطهٔ 0 = z تابع را چنین نشان میدهیم:
روش دیگر برای گسترش تابع علامت هم بر روی عددهای حقیقی و هم مختلط، به کار گرفتن csgn است[3] که به صورت زیر تعریف میشود:
که در آن بخش حقیقی z و بخش موهومی آن است.
در نتیجه در تمام نقطهها جز 0 = z خواهیم داشت:
تابع علامت در حالت کلی
به ازای مقدارهای حقیقی میتوان نسخهٔ تابع عمومی برای تابع علامت تعریف کرد و نام را بر آن گذاشت. که در آن در همه جا حتی در نقطهٔ (این قسمت برخلاف تابع است چون ) چنین عمومیسازی اجازهٔ کار بر روی جبر تابعهای عمومی را میدهد اما این عمومیسازی به قیمت از دست رفتن خاصیت جابجایی تمام میشود. به ویژه تابع علامت تعمیم یافته با تابع دلتا ویژگی ناجابجایی دارد:[4]
همچنین در تعریف نشدهاست. کاربرد نام ویژهٔ در این جا ضروری است تا با اشتباه گرفته نشود. ( تعریف نشدهاست ولی )
جستارهای وابسته
منابع
- احمد قندهاری، حمیدرضا امیری. تابع. انتشارات مدرسه. تهران.
- Sign - from Wolfram MathWorld
- Heaviside Step Function - from Wolfram MathWorld
- Maple V documentation. May 21, 1998
- Yu.M.Shirokov (1979). "Algebra of one-dimensional generalized functions". TMF. 39 (3): 471–477. doi:10.1007/BF01017992.
