توزیع بتا
توزیع بتا، توزیع احتمال پیوستهای است که بر بازه [۱و۰] تعریف میگردد و به توزیع گاما مرتبط میباشد.توزیع بتا دارای دو پارامتر آزاد است که این دو پارامتر شامل و میشوند.تابع چگالی احتمال این توزیع در زیر آوردهشده است.
|
تابع چگالی احتمال 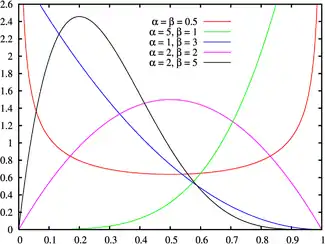 | |||
|
تابع توزیع تجمعی 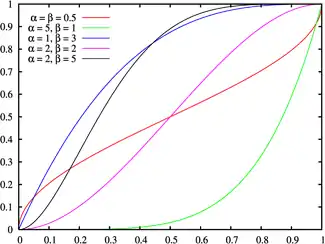 | |||
| فراسنجهها |
شکل (حقیقی) شکل (حقیقی) | ||
|---|---|---|---|
| تکیهگاه | |||
| تابع چگالی احتمال | |||
| تابع توزیع تجمعی | |||
| میانگین | |||
| مُد | for | ||
| واریانس | |||
| چولگی | |||
| کشیدگی | see text | ||
| آنتروپی | see text | ||
| تابع مولد گشتاور | |||
| تابع مشخصه | |||
کاربردها
آماره ترتیبی
توزیع بتا نقش مهمی در تئوری آماره ترتیبی دارد.نتیجه بدینگونه است که توزیع kمین کوچکترین مقدار از یک فضای نمونه nتایی از یک توزیع یکنواخت پیوسته معادل با یک توزیع بتا میباشد.نتیجه به صورت زیر خلاصه میگردد.
آنالیز موجکی
موجک یک نوسان موجمانند با دامنهای است که از صفر شروع میگردد، افزایش مییابد و سپس به صفر تقلیل مییابد.بهطور معمول موجکها را میتوان به عنوان نوسان مختصری که به سرعت در حال فروپاشی هستند تجسم کرد.موجکها میتوانند برای استخراج اطلاعات از انواع مختلف داده استفاده گردند.از جمله این دادهها میتوان به سیگنالها و تصاویر صوتی اشاره نمود.به این ترتیب، موجکها با این هدف ساخته میشوند تا ویژگیهای خاصی داشته باشند که آنها را قادر به پردازش سیگنال سازد.نکتهای که موجکها را برجسته میسازد این است که آنها هم در زمان و هم در فرکانس موضعی میباشند در حالی که تبدیل استاندارد فوریه تنها در فرکانس موضعی است.بنابراین، تبدیل استاندارد فوریه فقط برای فرایندهای ثابت قابل استفاده است در حالی که موجکها برای فرآیندهای غیرثابت نیز قابل استفاده میباشند.موجکها را میتوان بر اساس توزیع بتا ساخت.موجک ساختهشده توسط توزیع بتا را میتوان به عنوان یک طیف نرم از موجهای هار مشاهده کرد که شکل آن با دو پارامتر α و β مشخص میگردد.[1]
آنالیز بیزی
یکی از مهمترین کاربردهای توزیع بتا استفاده از آن در آنالیز آماری بیزی توزیع دوجملهای است.درواقع توزیع بتا به عنوان یک مدل برای احتمال موفقیت یک توزیع دوجملهای استفاده میگردد،به این صورت که توزیع بتا به عنوان یک توزیع پیشین یا پسین برای آنالیز مورد استفاده قرار میگیرد.[2]
مشخصات
تابع چگالی احتمال(PDF)
تابع توزیع تجمعی احتمال(CDF)
ویژگیها
مد
میانه
میانگین
توزیعهای مرتبط
توزیع بتاپریم
اگر X از توزیع بتا پیروی نماید آنگاه با استفاده از تبدیل (T = X/(1-X به توزیعی با چگالیاحتمال زیر دست مییابیم.
این توزیع یک فرم استاندارد از توزیع پیرسون نوع ۶ که گاهی اوقات به نام توزیع بتاپریم شناخته میشود میباشد.
توزیع یکنواخت
اگر با این فرض که , مقادیر صحیح مثبتی هستند که جمع این دو برابر با مقدار ثابت s میباشد().با این فرض مقادیر 1 تا s-1 را میتواند به خود اختصاص دهد. تابع چگالی احتمال X با فرضهای ذکر از رابطه زیر به دست میآید.
این توزیع شرطی از توزیع یکنواخت پیوسته پیروی مینماید.اگر شروط ذکرشده در بالا برقرار باشند.
منابع
- Weisstein, Eric W. "Beta Distribution". mathworld.wolfram.com. Retrieved 2018-12-27.
- «probability - Applications of Beta Distribution». Mathematics Stack Exchange. دریافتشده در ۲۰۱۸-۱۲-۲۷.
- مشارکتکنندگان ویکیپدیا. «Beta distribution». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲۹ می ۲۰۱۱.
