آنتروپی اطلاعات

آنتروپی متغیر تصادفی گسستهٔ ${\displaystyle X}$ با تابع جرم احتمال ${\displaystyle P(X)}$ را با نماد ${\displaystyle \mathrm {H} (X)}$ نمایش می‌دهند و به صورت زیر تعریف می‌شود:

${\displaystyle \mathrm {H} (X)=\mathrm {E} [\mathrm {I} (X)]=\mathrm {E} [-\log _{b}(\mathrm {P} (X))].}$

در رابطهٔ بالا ${\displaystyle \mathrm {E} [\cdot ]}$ تابع امید ریاضی و ${\displaystyle \mathrm {I} (\cdot )}$ تابع میزان اطلاعات رویداد است. ${\displaystyle \mathrm {I} (X)}$ تابعی از یک متغیر تصادفی و در نتیجه یک متغیر تصادفی است. ${\displaystyle b}$ پایهٔ لگاریتم است و مقادیر مختلف آن آنتروپی را در واحدهای متفاوتی محاسبه می‌کند. متداول‌ترین مقادیر برای ${\displaystyle b}$ ، ۲ و e و ۱۰ هستند که به ترتیب آنتروپی را در واحدهای بیت و nat و hartley محاسبه می‌کند.

می‌توان آنتروپی ${\displaystyle X}$ را به صورت باز هم نوشت:

${\displaystyle \mathrm {H} (X)=\sum _{i=1}^{n}{\mathrm {P} (x_{i})\,\mathrm {I} (x_{i})}=-\sum _{i=1}^{n}{\mathrm {P} (x_{i})\log _{b}\mathrm {P} (x_{i})}.}$

همچنین مقدار ${\displaystyle \mathrm {I} (0)=0\times log(0)}$ را صفر تعریف می‌کنیم که با مشاهدهٔ ${\displaystyle \lim _{p\to 0+}p\log(p)=0}$ نیز سازگار است.

آنتروپی متغیر تصادفی ${\displaystyle X}$ به شرط ${\displaystyle Y}$ با توزیع احتمال مشترک ${\displaystyle P(X,Y)}$ نیز به صورت زیر تعریف می‌شود:

${\displaystyle \mathrm {H} (X|Y)=-\sum _{i,j}P(x_{i},y_{j})\log {\frac {P(x_{i},y_{j})}{P(y_{j})}}}$

${\displaystyle \mathrm {H} (X|Y)}$ میانگین اطلاعات حاصل از مشاهدهٔ ${\displaystyle X}$ به شرط اطلاع از ${\displaystyle Y}$ را نشان می‌دهد.

نمودار آنتروپی نتیجهٔ پرتاب یک سکه در واحد بیت بر حسب احتمال شیر آمدن آن. هر چقدر احتمال شیر آمدن سکه به ۰٫۵ نزدیکتر باشد ابهام در مورد نتیجهٔ آن بیشتر است و اطلاع از نتیجه، به‌طور میانگین اطلاعات بیشتری دربردارد.

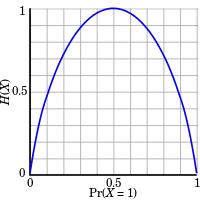
متغیر تصادفی ${\displaystyle X}$ را برابر با نتیجهٔ پرتاب یک سکه در نظر بگیرید که با احتمال ${\displaystyle p}$ شیر و با احتمال ${\displaystyle 1-p}$ خط می‌آید. هرچقدر ${\displaystyle p}$ به ${\displaystyle 1 \over 2}$ نزدیکتر باشد، ابهام در مورد نتیجهٔ پرتاب بیشتر است و به همین ترتیب اطلاع از نتیجهٔ پرتاب به‌طور میانگین اطلاعات بیشتری دربردارد. در واقع بیشترین میزان آنتروپی برای حالت ${\displaystyle p={1 \over 2}}$ و برابر با ۱ بیت است:

${\displaystyle \mathrm {H} (X)=-\sum _{i=1}^{n}{\mathrm {P} (x_{i})\log _{2}\mathrm {P} (x_{i})}=-\sum _{i=1}^{2}{{1 \over 2}\log _{2}({1 \over 2})}=1,}$

در حالتی که ${\displaystyle p}$ صفر یا یک باشد، هیچ ابهامی در مورد نتیجهٔ پرتاب وجود ندارد و به همین ترتیب اطلاع از نتیجهٔ پرتاب هیچ اطلاعاتی در برندارد:

${\displaystyle \mathrm {H} (X)=-\left({{0}\log _{2}({0})}+{{1}\log _{2}({1})}\right)=0.}$

برای حالت ${\displaystyle p={1 \over 4}}$ انتظار داریم آنتروپی کمتر از حالت یکنواخت و بیشتر از حالت بدون ابهام باشد:

${\displaystyle \mathrm {H} (X)=-\left({{1 \over 4}\log _{2}({1 \over 4})}+{{3 \over 4}\log _{2}({3 \over 4})}\right)\approx 0.81}$

به‌طور کلی بیشترین میزان آنتروپی برای یک متغیر تصادفی در توزیع یکنواخت و کمترین میزان آنتروپی در توزیعی با یک رویداد قطعی رخ می‌دهد.

آنتروپی یک منبع اطلاعات، حد پایین متوسط بهترین نرخ فشرده‌سازی بدون اتلاف داده‌های آن منبع است. به بیان دقیق‌تر هیچ روش فشرده‌سازی ای وجود ندارد که به‌طور میانگین مقدار متغیر تصادفی ${\displaystyle X}$ را با کمتر از ${\displaystyle \mathrm {H} (X)}$ بیت فشرده کند. این حد پایین بسیار قوی است، به‌طوری که برای دنباله‌های به طول ${\displaystyle n}$ از داده‌های هر منبع تصادفی ${\displaystyle X}$، یک روش فشرده‌سازی وجود دارد که به‌طور میانگین، نتیجه هر مشاهده را حداکثر با ${\displaystyle \mathrm {H} (X)+{1 \over n}}$ بیت فشرده می‌کند.

• Elements of Information Theory (انگلیسی)