عدد پی
عدد (با تلفظ /paɪ/ در انگلیسی و «پی» در فارسی)، یک ثابت ریاضیاتی است. این ثابت به صورت نسبت محیط دایره به قطرش تعریف شده و تعاریف معادل مختلفی نیز دارد. این عدد در بسیاری از فرمولهای ریاضیاتی، در تمام زمینههای ریاضیات و فیزیک ظاهر میشود. قدیمیترین استفاده از حرف یونانی جهت نمایش نسبت محیط دایره به قطرش، توسط ریاضیدان ویلزی به نام ویلیام جونز در ۱۷۰۶ میلادی بر میگردد.[1] این ثابت تقریباً برابر با ۳٫۱۴۱۵۹ بوده و برخی مواقع به آن ثابت ارشمیدس هم گفته میشود.[2][3][4]
| بخشی از سری مقالات در مورد: |
| ثابت ریاضی |
|---|
 |
| کاربردها |
|
| خواص |
|
| مقدار |
|
| افراد |
|
| تاریخچه |
|
| در فرهنگ |
|
| موضوعات مرتبط |
|
از آنجا که یک عدد گنگ است، نمیتوان آن را به صورت کسر متعارفی بیان کرد، گرچه که کسرهایی چون را اغلب جهت تخمین آن به کار میبرند. گنگ بودن آن را میتوان بهطور معادل اینگونه بیان کرد: نمایش مبنای ده (دسیمال) آن پایان ناپذیر بوده و هیچگاه الگوی تا ابد تکرار شونده ای نخواهد داشت. ارقام مبنای ده (و مبناهای دیگر) آن ظاهراً تصادفی بوده و حدس زده میشود که در نوع خاصی از تصادفی بودن آماری صدق میکند.
مشخص شده که یک عدد متعالی است:[3] یعنی ریشه هیچ چندجمله ای با ضرایب گویا نیست. متعالی بودن ایجاب میکند که حل چالش باستانی تربیع دایره با خطکش و پرگار غیرممکن باشد.
تمدنهای باستانی شامل مصریان و بابلیان، نیاز به تخمینهای نسبتاً دقیقی از برای محاسبات عملی داشتند. حدود ۲۵۰ قبل از میلاد بود که ریاضیدان یونانی به نام ارشمیدس، الگوریتمی را جهت تخمین با دقت دلخواه ایجاد کرد. در قرن پنجم بعد از میلاد، ریاضیدانان چینی عدد را تا هفت رقم اعشار تخمین زدند، در حالی که ریاضیدانان هندی به تخمین پنج رقمی دست یافته و هردو نیز از فنون هندسی در این تخمینها بهره جستند. اولین فرمول دقیق برای ، بر اساس سریهای نامتناهی بود که هزار سال بعد کشف شد. این کشف در ریاضیات هند و طی کشف سری ماداوا-لایبنیتس (Madhava-Leibniz) حاصل شد.[5][6]
به زودی، ابداع حسابان منجر به محاسبه صدها رقم از شد که جهت استفاده در تمامی انواع محاسبات علمی کفایت میکرد. با این حال، در قرن ۲۰م و ۲۱م میلادی، ریاضیدانان و دانشمندان کامپیوتری به دنبال رهیافتهای تازه ای رفتهاند که در ترکیب با افزایش قدرت محاسباتی، نمایش ارقام را به چندین تریلیون رقم توسعه دادهاند.[7][8] در حقیقت انگیزه اولیه و اصلی محاسبات جهت یافتن ارقام عدد ، تبدیل این فرایند به نمونه آزمایشی جهت توسعه الگوریتمهای کارا برای محاسبه سریهای عددی، و همچنین عطش شکستن رکوردهاست.[9][10] چنین محاسبات گستردهای که در این فرایند به کار میرود، جهت آزمودن سوپرکامپیوترها و الگوریتمهای ضرب با دقت بالا نیز به کار رفتهاند.
از آنجا که مقدماتیترین تعریف عدد ، مربوط به دایره است، انبوهی از فرمولهای مثلثاتی و هندسی دیگری نیز که برای آن یافته شده، فرمولهایی اند که با دایرهها، بیضیها و کرهها در ارتباط اند. در آنالیز ریاضی مدرن تر، این عدد با استفاده از خواص طیفی دستگاه اعداد حقیقی، به صورت مقدارویژه یا تناوب توابع تعریف میگردد، بدون ارجاعی به هندسه. بنابر این در حوزههایی از ریاضیات و علوم که در ظاهر ارتباط کمی با هندسه و دایره دارند، همچون نظریه اعداد و آمار و همچنین تقریباً در تمامی شاخههای فیزیک، عدد ظهور پیدا میکند. حضور در همه جا، هم در داخل جامه علمی و هم خارج آن، باعث شده که این عدد تبدیل به یکی از معروفترین ثوابت ریاضیاتی گردد.
مقدمات
نام
نمادی که ریاضیدانان برای نمایش نسبت محیط دایره به قطر آن به کار میبرند حرف کوچک یونانی است که «پی» تلفظ میشود و حرف اول کلمهٔ یونانی «پریمتروس»[persian-alpha 1] (به معنی محیط) است.[11] کاربرد ریاضیاتی حرف کوچک پی (یا π در قلمهای سنزسریف) با کاربرد حرف بزرگ پی (یعنی ∏) فرق دارد. حرف بزرگ پی برای نمایش ضرب دو دنباله استفاده میشود و کاربرد آن مشابه کاربرد ∑ در مجموعیابی است.
تعریف

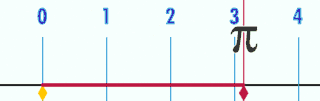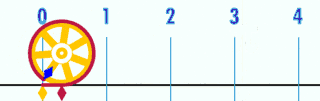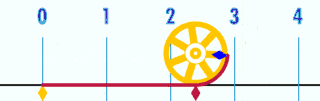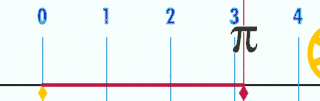
غالباً بهعنوان نسبت محیط یک دایره به قطر تعریف میشود. یعنی:[12]
نسبت صرفنظر از اندازهٔ دایره ثابت است. مثلاً اگر قطر دایره دو برابر شود، محیط آن هم دو برابر خواهد شد و نسبت ثابت خواهد ماند. این تعریف بهشکل ضمنی از هندسه اقلیدسی (مسطح) استفاده میکند؛ یعنی بااینکه مفهوم دایره را میتوان به هندسه نااقلیدسی تعمیم داد، این «دایره»ها دیگر لزوماً در معادلهٔ صدق نخواهند کرد.[12]
مقدار محیط دایره برابر است با طول قوسی که پیرامون دایره قرار دارد و این کمیت را میتوان مستقل از هندسه و با استفاده از مفهوم حددر حساب دیفرانسیل و انتگرال محاسبه کرد.[13] برای مثال، میتوان طول قوس نیمهٔ بالایی دایرهٔ واحد، که معادلهٔ آن در دستگاه مختصات دکارتی برابر با x2 + y2 = ۱است، را مستقیماً به شکل انتگرال زیر انتگرال حساب کرد:[14]
این تعریف با استفاده از انتگرال را نخستین بار کارل وایرشتراس در ۱۸۴۱ به کار برد.[15]
تعریف دیگری از عدد پی:
این گونه تعاریف پی که به مفهوم محیط و بهشکلی ضمنی به انتگرال وابستهاند امروزه در ادبیات علمی رایج نیستند. به گفتهٔ راینهولد رمرت دلیل آن این است که در آموزش حسابان در مدارس حساب دیفرانسیل معمولاً پیش از حساب انتگرال قرار میگیرد و از این رو به تعریفی از نیاز است که به دومی وابسته نباشد.[16] یکی از این تعریفها، که به ریچارد بالتزر[persian-alpha 2] منسوب است[17] و ادموند لانداوآن را مشهور کردهاست،[18] از این عبارت است: دو برابر کوچکترین عددی است که در آن تابع کسینوس برابر ۰ است.[12][14][19] کسینوس را میتوان مستقل از هندسه به عنوان یک سری توانی,[20] یا بهعنوان ریشهٔ یک معادله دیفرانسیل تعریف کرد.[19]
به همین ترتیب، , را میتوان با استفاده از ویژگیهای تابع نمایی مختلط، exp(z), ار متغیر مختلط z تعریف کرد. مانند کسینوس، تابع نمایی مختلط را میتواند به چند شکل تعریف کرد. ازینرو مجموعهٔ اعداد مختلطی که در آن exp(z) برابر یک است عبارت خواهد بود از یک تصاعد حسابی (موهومی) به صورت:
و فقط یک عدد حقیقی با این ویژگی وجود دارد.[14][21] گونهای انتزاعیتر از همین ایده، که از مفاهیم پیچیدهٔ ریاضیاتی توپولوژی وجبر استفاده میکند، قضیهٔ ذیل است:[22] تنها یک (به تقریب خودریختی) تابع پیوسته یکریختی وجود دارد که دامنهاش گروه R/Z از اعداد حقیقی تحت اعداد صحیح گروه دایره (en) و بردش گروه ضربی اعداد مختلط قدر مطلق یک باشد و عدد برابر نصف بزرگی مشتق این همریختی است.[23]
گنگ بودن و نرمال بودن
عددی گنگ است؛ یعنی نمیتوان آن را به صورت یک عدد گویا (نسبت دو عدد صحیح) نوشت. گاه از کسرهایی مثل برای تقریب استفاده میشود، ولی هیچ کسری برابر مقدار دقیق نیست.[24] از آنجا که گنگ است، نمایش دهدهی آن تعداد نامتناهی رقم دارد و به شکل مختوم یا دهدهی متناوب نیست. اثباتهای مختلفی برای گنگ بودن وجود دارد که غالباً مبتنی بر استفاده از حسابان و روشهای تعلیق به محالند. هنوز معلوم نیست که را تا به چه اندازهای میتوان با استفاده از عدد گویا تقریب کرد (مقیاس گنگی آن محاسبه نشدهاست)؛ ولی بنابر تخمینها مقیاس گنگی آن از مقیاس گنگی یا بزرگتر ولی از مقیاس گنگی اعداد لیوویل کوچکتر است.[25]
ارقام اعشار هیچ الگوی مشخصی ندارند و شرایط تصادف آماری و اعداد نرمال را احراز میکنند.[26] با این حال نرمال بودن ثابت نشدهاست.[26] با ابداع کامپیوتر، تعداد انبوهی از ارقام برای تحلیلهای آماری در دسترس ریاضیدانان قرار گرفت. یاسوماسا کانادا با انجام تحلیلهای آماری روی ارقام آنها را با شرایط نرمال هماهنگ دانست و نشانی از وجود الگو در آنها نیافت.[27] بنابر قضیه میمون نامتناهی، هر وقت دنبالهای تصادفی از ارقام به اندازه کافی بزرگ باشد، بخشی از آن شامل دنبالههایی است که به نظر غیر تصادفی میرسند. یک نمونهٔ دنبالههای تصادفی در دنبالهٔ ارقام که به نظر غیرتصادفی میرسند از رقم ۷۶۲م در نمایش اعشاری آغاز میشود و در فولکلور ریاضی به نقطه فاینمن موسوم است.[28]
تعالی
میتوان ثابت کرد که یکی از عددی متعالیاست، به این معنی که هیچ معادله جبری غیرثابت با ضرایب گویا (مثلاًx5120 − x36 + x = ۰) وجود ندارد که جوابش پی باشد.[29][persian-alpha 3]
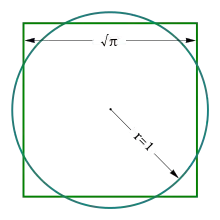
از تعالی دو نتیجهٔ مهم میشود گرفت: یکی اینکه را نمیتوان با استفاده از ترکیب متناهی اعداد گویا و ریشهٔ دوم (مانند3√31 یا √10) بیان کرد. ثانیاً از آنجا که اعداد متعالی ترسیمپذیر نیستند، تربیع دایره با استفاده از خطکش و پرگار غیرممکن است، یعنی نمیتوان تنها با استفاده از خطکش و پرگار مربعی رسم کرد که مساحت آن برابر مساحت دایرهای معین باشد.[30] تربیع مربع یکی از مهمترین مسائل هندسی در گذر تاریخ بودهاست[31] و با اینکه در ۱۸۸۲ فردیناند فون لیندمن نشان داد که پی عددی متعالی است و تربیع دایره غیرممکن است، هنوز برخی ریاضیدانان آماتور تلاش میکنند آن را حل کنند و گاه ادعا میکنند آن را حل کردهاند.[32]
کسرهای مسلسل

مانند همهٔ اعداد گنگ، ثابت نمیتوان به صورت یک کسر متعارفی ساده (کسر معمولی، که صورت و مخرج آن اعداد صحیح هستند) نمایش داد. بااینحال همهٔ اعداد گنگ، از جمله را میتوان با استفاده از سلسلهای نامتناهی از کسرهای تودرتو، موسوم به کسر مسلسل، نشان داد:
با قطع کردن این کسر مسلسل در هر مرحله، میتوان تقریبی گویا از بهدستآورد؛ چهار انقطاع و تقریب گویای اول این کسر مسلسل عبارتند از ۳، ۲۲/۷، ۳۳۳/۱۰۶، و ۳۵۵/۱۱۳. این اعداد شناختهشدهترین و پراستفادهترین تقریبهای عدد پی هستند. هر تقریبی که به این شکل بهدست بیاید «بهترین تقریب گویا» در آن مخرج است، به این مفهوم که از هر عدد گویا با مخرج برابر یا کمتر به نزدیکتر است.[33] از آنجا که عددی متعالی است، بنابر تعریف عدد جبری نیست و نمیتواند عدد گنگ درجه دو باشد. ازینرو کسر مسلسل دورهای ندارد. بااینکه در کسر مسلسل معمولی (که در بالا آمدهاست) هیچ الگوی مشخصی نیست،[34] ریاضیدانان چند کسر مسلسل عام (کسر مسلسلی با صورت یا مخرج مختلط) برای آن کشف کردهاند که الگوی مشخصی دارند، ازآنجمله:[35]
تقریب و ارقام
ارقام در دستگاههای اعداد دیگر
- ۴۸ رقم اعشاری در دستگاه اعداد دودویی (مبنای ۲) عبارتند از: ۱۱٫۰۰۱۰۰۱۰۰۰۰۱۱۱۱۱۱۰۱۱۰۱۰۱۰۱۰۰۰۱۰۰۰۱۰۰۰۰۱۰۱۱۰۱۰۰۰۱۱٫٫٫
- ۲۰ رقم اول اعشاری در دستگاه اعداد هِگزادِسیمال (مبنای ۱۶) عبارتند از۳٫۲۴۳F۶A۸۸۸۵A۳۰۸D۳۱۳۱۹٫٫٫[37]
- پنج رقم اول در دستگاه اعداد شصتشصتی (مبنای ۶۰) عبارتند از ۳;۸٬۲۹٬۴۴٬۰٬۴۷[38]
اعداد مختلط و اتحاد اویلر
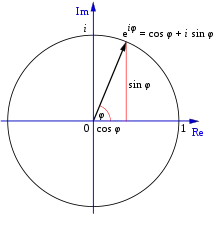
هر عدد مختلط z میتوان با استفاده از دو عدد حقیقی نمایش داد. در دستگاه مختصات قطبی، یک (شعاع یا r) برای نمایش فاصلهٔ z از مبدأ مختصاتی صفحه مختلط و عدد دیگر (زاویه یا φ) برای نمایش چرخشی در خلاف جهت عقربههای ساخت از خط حقیقی مثبت به شکل زیر استفاده میشود:[39]
که در آن i یکه موهومیای است که در i2 = −۱ صدق میکند. حضور مداوم در آنالیز مختلط را میتوان با رفتار تابع نمایی متغیر مختلط مرتبط دانست، که بهشکل زیر با فرمول اویلر توصیف میشود:[40]
که در آن عدد e پایهٔ لگاریتم طبیعی است. این فرمول رابطهای بین توانهای موهومی e و نقاط روی محیط دایره واحد که مرکز در مبدأ مختصاتی صفحهٔ مختلط قرار دارد برقرار میکند. با قرار دادن φ = در فرمول اویلر میتوان اتحاد اویلر را بهدستآورد. سرشناسی این اتحاد نزد ریاضیدانان از آن رو است که پنج تا از مهمترین ثابتهای ریاضی را در خود دارد:[40][41]
n تا عدد مختلط z وجود دارد که در رابطهٔ zn = ۱ صدق کند، و اینها به «ریشه واحد nم» موسومند[42] و از طریق فرمول:
محاسبه میشوند.
تاریخچه
در بابل کهن بین ۱۶۰۰ تا ۱۹۰۰ سال پیش از میلاد عدد پی را به صورت ۲۵۸ = ۳٫۱۲۵ تخمین زدند. در مصر باستان نیز بین ۱۶۰۰ تا ۱۸۵۰ سال پیش از میلاد (۱۶۹)۲ ≈ ۳٫۱۶۰۵ برآورد کردند.[43] عدد پی عدد پی حدود چهار هزار سال پیش نیز کشف شده بود، ولی نام خاصی برای آن تعیین نشده بود و در آن زمان نمیدانستند که عدد پی، عددی گنگ است. یکی از نظریهها راجع به مساحت دایره بودهاست که نمایان گر آن است عدد پی را به صورت نامحسوسی کشف کرده بودند؛ این نظریهٔ پاپیروس است که میگفت: اگر قطر دایره ای را به نه قسمت مساوی تقسیم کنیم و یک قسمت از آن را حذف کنیم، مربعی به ضلع آن، مساحتی برابر با مساحت آن دایره دارد. با این حساب عدد پی به صورت یک عبارت گویا و به صورت اعشاری تقریباً برابر است با "۳٫۱۶" که این عدد خیلی به عدد پی نزدیک است و دقتی تا این حد در آن زمان بسیار جالب توجه است. البته این قبل از آن است که مشخص شود عدد پی گنگ است.[44]
تقریب اعشاری عدد پی
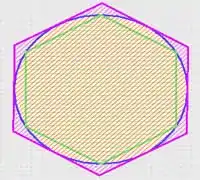
پس از آن که مشخص شد که عدد پی، عددی گنگ است؛ اولین نظریه در مورد مقدار تقریبی عدد پی توسط ارشمیدس بیان شد. این نظریه بر پایه تقریب زدن مساحت دایره به وسیلهٔ یک شش ضلعی منتظم محیطی و یک شش ضلعی منظم محاطی استوار است.[44]
ریاضیدانان اروپایی در قرن هفدهم به مقدار واقعی عدد پی نزدیکتر شدند. از جمله این دانشمندان جیمز گریگوری بود که برای پیدا کردن مقدار عدد پی از فرمول زیر استفاده کرد:
یکی از مشکلاتی که در این روش وجود دارد این است که برای پیدا کردن مقدار عدد پی تا ۶ رقم اعشار باید پنج میلیون جمله از سری فوق را با هم جمع کنیم.
طبق محاسبهٔ کامپیوتری سری فوق، تعداد سری و اعشار محاسبه شده مطابق زیر است:
- ۱۰۰ میلیون جمله: ۷ رقم اعشار
- یک میلیارد جمله: ۸ رقم اعشار
ارقام بالا نشان میدهد که این الگوریتم رشد نمایی شدیدی دارد که زمان زیادی را میتواند برای محاسبهٔ ارقام بسیار بالا صرف نماید.
در سال ۱۷۶۱ لامبرت ریاضیدان سوئیسی ثابت کرد که عدد پی گنگ است و نمیتوان آن را به صورت نسبت دو عدد صحیح نوشت. همچنین در سال ۱۸۸۲ فردیناند فون لیندمان ثابت کرد که عدد پی یک عدد جبری نیست و نمیتواند ریشه یک معادله جبری باشد که ضرایب آن گویا هستند (همانند عدد e). کشف گنگ بودن عدد پی، به سالها تلاش ریاضیدانان برای تربیع دایره پایان داد.
در اوایل قرن هجدهم ریاضیدان دیگری به نام جان ماشین فرمول گریگوری را اصلاح کرد که این فرمول امروزه نیز در برنامههای رایانهای برای محاسبه عدد پی مورد استفاده قرار میگیرد. این فرمول به صورت زیر است:
با استفاده از این فرمول یک انگلیسی به نام ویلیام شانکس مقدار عدد پی را تا ۷۰۷ رقم اعشار محاسبه کرد، در حالیکه فقط ۵۲۷ رقم آن درست بود.
با آن که همه ریاضیدانان میدانند که عدد پی گنگ است و هرگز نمیتوان آن را به طور دقیق محاسبه کرد اما ارائه فرمولها و مدلهای محاسبه عدد پی همواره برای آنها از جذابیت برخوردار بوده است. بسیاری از آنها همه عمر خود را صرف محاسبه ارقام این عدد کردند اما هرگز نتوانستند تا پیش از ساخته شدن کامپیوتر این عدد را بیش از هزار رقم اعشار محاسبه کنند.
امروزه مقدار عدد پی با استفاده از پیشرفتهترین رایانهها تا میلیونها رقم محاسبه شدهاست و تعداد این ارقام هنوز در حال افزایش است. اولین محاسبه کامپیوتری در سال ۱۹۴۹ انجام گرفت و این عدد را تا ۲۰۰۰ رقم محاسبه کرد و در اواخر سال ۱۹۹۹ یکی از سوپر کامپیوترهای دانشگاه توکیو این عدد را تا ۲۰۶٬۱۵۸٬۴۳۰٬۰۰۰ رقم اعشار محاسبه کرد.
از سال ۱۹۸۸ روز ۱۴ مارس را در آمریکا روز عدد پی نام نهادهاند و جشن میگیرند. روزهای دیگری نیز برای عدد پی در دیگر کشورها تعیین شده و مراسمی برای معرفی عدد پی و اهمیت آن برگزار میشود.
عدد پی در ایران
در قرن نهم هجری، غیاثالدین جمشید کاشانی، ریاضیدان دانشمند ایرانی، در رسالة المحیطیه که دربارهٔ دایره نوشت، عدد پی را با ۱۶ رقم درست پس از ممیز یافت که تا ۱۸۰ سال بعد کسی نتوانست آن را گسترش دهد.
فهرست اعداد – اعداد گنگ | |
| دودویی | ۱۱٫۰۰۱۰۰۱۰۰۰۰۱۱۱۱۱۱۰۱۱۰… |
| دهدهی | ۳٫۱۴۱۵۹۲۶۵۳۵۸۹۷۹۳۲۳۸۴۶… |
| دوازدهدوازدهی | ۳٬۱۸۴۸۰۹۴۹۳B۹۱۸۶۴… |
| شانزدهشانزدهی | ۳٫۲۴۳F6A8885A308D۳۱۳۱۹… |
| کسر متناوب | Note that this continued fraction is not periodic. |
در رسانه
- در سال ۱۹۹۸ فیلمی به همین نام یعنی پی ساخته شد.
- ستون های تخت جمشید بر اساس عدد پی ساخته شده
- سریالی به نام «نردبام آسمان» درباره زندگی کاشف ایرانی عدد پی
کاربرد
مرتبط: List of formulae involving π (en) از آنجا که ارتباط نزدیکی با دایره دارد، میتوان در بسیاری از فرمولهای هندسه و مثلثات، به ویژه فرمولهایی که مربوط به دایره، کره، یا بیضی میشوند رد پای آن را دید. همچنین در فرمولهای دیگر علوم از جمله ریاضیات تحلیلی، نظریه اعداد، فیزیک، آمار، احتمالات، مهندسی، و زمینشناسی دیده میشود.
جستارهای وابسته
یادداشتها
ارجاعات
- Jones, William (1706). Synopsis Palmariorum Matheseos: or, a New Introduction to the Mathematics. pp. 243, 263. Archived from the original on 25 March 2012. Retrieved 15 October 2017.
- "Compendium of Mathematical Symbols". Math Vault. 2020-03-01. Retrieved 2020-08-10.
- Weisstein, Eric W. "Pi". mathworld.wolfram.com. Retrieved 2020-08-10.
- Bogart, Steven. "What Is Pi, and How Did It Originate?". Scientific American. Retrieved 2020-08-10.
- Andrews, Askey & Roy 1999, p. 59.
- Gupta 1992, pp. ۶۸–۷۱.
- "πe trillion digits of π". pi2e.ch. Archived from the original on 6 December 2016.
- Haruka Iwao, Emma (14 March 2019). "Pi in the sky: Calculating a record-breaking 31.4 trillion digits of Archimedes' constant on Google Cloud". Google Cloud Platform. Archived from the original on 19 October 2019. Retrieved 12 April 2019.
- Arndt & Haenel 2006, p. 17.
- Bailey et al. 1997, pp. ۵۰–۵۶.
- Boeing, Niels (14 March 2016). "Die Welt ist Pi" [The World is Pi]. Zeit Online (به آلمانی). Archived from the original on 17 March 2016.
Die Ludolphsche Zahl oder Kreiszahl erhielt nun auch das Symbol, unter dem wir es heute kennen: William Jones schlug 1706 den griechischen Buchstaben π vor, in Anlehnung an perimetros, griechisch für Umfang. Leonhard Euler etablierte π schließlich in seinen mathematischen Schriften. [The Ludolphian number or circle number now also received the symbol under which we know it today: William Jones proposed in 1706 the Greek letter π, based on perimetros [περίμετρος], Greek for perimeter. Leonhard Euler firmly established π in his mathematical writings.]
- Arndt & Haenel 2006, p. 8
- Apostol, Tom (1967). Calculus, volume 1 (2nd ed.). Wiley.. p. 102: "From a logical point of view, this is unsatisfactory at the present stage because we have not yet discussed the concept of arc length." Arc length is introduced on p. 529.
- Remmert, Reinhold (1991), "", Numbers, Springer, p. 129
- Remmert (1991). انتگرال دقیق وایرشتراس عبارت است از
- Remmert 1991.
- Baltzer, Richard (1870), Die Elemente der Mathematik [The Elements of Mathematics] (به آلمانی), Hirzel, p. 195, archived from the original on 14 September 2016
- Landau, Edmund (1934), Einführung in die Differentialrechnung und Integralrechnung (به آلمانی), Noordoff, p. 193
- Rudin, Walter (1976). Principles of Mathematical Analysis. McGraw-Hill. ISBN 978-0-07-054235-8., p. 183.
- Rudin, Walter (1986). Real and complex analysis. McGraw-Hill., p. 2.
- Ahlfors, Lars (1966), Complex analysis, McGraw-Hill, p. 46
- Bourbaki, Nicolas (1981), Topologie generale, Springer, §VIII.2.
- Bourbaki, Nicolas (1979), Fonctions d'une variable réelle (به فرانسوی), Springer, §II.3.
- Arndt & Haenel 2006, p. 5
- Salikhov, V. (2008). "On the Irrationality Measure of pi". Russian Mathematical Surveys. 53 (3): 570–572. Bibcode:2008RuMaS..63..570S. doi:10.1070/RM2008v063n03ABEH004543.
- Arndt & Haenel 2006, pp. 22–23
Preuss, Paul (23 July 2001). "Are The Digits of Pi Random? Lab Researcher May Hold The Key". آزمایشگاه ملی لارنس برکلی. Archived from the original on 20 October 2007. Retrieved 10 November 2007. - Arndt & Haenel 2006, pp. 22, 28–30
- Arndt & Haenel 2006, p. 3
- Mayer, Steve. "[[عدد پی|]]". Archived from the original on 2000-09-29. Retrieved 4 November 2007. URL–wikilink conflict (help)
- Posamentier & Lehmann 2004, p. 25
- Eymard & Lafon 1999, p. 129
- Beckmann 1989, p. 37
Schlager, Neil; Lauer, Josh (2001). Science and Its Times: Understanding the Social Significance of Scientific Discovery. Gale Group. ISBN 978-0-7876-3933-4., p. 185. - Eymard & Lafon 1999, p. 78
- Sloane, N. J. A. (ed.). "Sequence A001203 (Continued fraction for Pi)". دانشنامه برخط دنبالههای صحیح. OEIS Foundation. Retrieved 12 April 2012.
- Lange, L.J. (May 1999). "". The American Mathematical Monthly. 106 (5): 456–458. doi:10.2307/2589152. JSTOR 2589152.
- Arndt & Haenel 2006, p. 240
- Arndt & Haenel 2006, p. 242
- Kennedy, E.S. (1978), "Abu-r-Raihan al-Biruni, 973–1048", Journal for the History of Astronomy, 9: 65, Bibcode:1978JHA.....9...65K, doi:10.1177/002182867800900106. Ptolemy used a three-sexagesimal-digit approximation, and Jamshīd al-Kāshī expanded this to nine digits; see Aaboe, Asger (1964), Episodes from the Early History of Mathematics, New Mathematical Library, 13, New York: Random House, p. 125, ISBN 978-0-88385-613-0, archived from the original on 29 November 2016
- Ayers 1964, p. 100
- Bronshteĭn & Semendiaev 1971, p. 592
- Maor, Eli, E: The Story of a Number, Princeton University Press, 2009, p. 160, شابک ۹۷۸−۰−۶۹۱−۱۴۱۳۴−۳ ("five most important" constants).
- Weisstein, Eric W. "Roots of Unity". MathWorld.
- Arndt & Haenel ۲۰۰۶, p. ۱۶۷
- JM فقط ریاضی بایگانیشده در ۲۱ ژوئن ۲۰۱۵ توسط Wayback Machine عدد پی
منابع
- Andrews, George E.; Askey, Richard; Roy, Ranjan (1999). Special Functions. Cambridge: University Press. ISBN 978-0-521-78988-2.
- Arndt, Jörg; Haenel, Christoph (2006). Pi Unleashed. Springer-Verlag. ISBN 978-3-540-66572-4. Retrieved 5 June 2013. English translation by Catriona and David Lischka.
- Ayers, Frank (1964). Calculus. McGraw-Hill. ISBN 978-0-07-002653-7.
- Bailey, David H.; Plouffe, Simon M.; Borwein, Peter B.; Borwein, Jonathan M. (1997). "The quest for PI". The Mathematical Intelligencer. 19 (1): 50–56. CiteSeerX 10.1.1.138.7085. doi:10.1007/BF03024340. ISSN 0343-6993. S2CID 14318695.
- Beckmann, Peter (1989) [1974]. History of Pi. St. Martin's Press. ISBN 978-0-88029-418-8.
- Berggren, Lennart; Borwein, Jonathan; Borwein, Peter (1997). Pi: a Source Book. Springer-Verlag. ISBN 978-0-387-20571-7.
- Boeing, Niels (14 March 2016). "Die Welt ist Pi" [The World is Pi]. Zeit Online (به آلمانی). Archived from the original on 17 March 2016.
Die Ludolphsche Zahl oder Kreiszahl erhielt nun auch das Symbol, unter dem wir es heute kennen: William Jones schlug 1706 den griechischen Buchstaben π vor, in Anlehnung an perimetros, griechisch für Umfang. Leonhard Euler etablierte π schließlich in seinen mathematischen Schriften. [The Ludolphian number or circle number now also received the symbol under which we know it today: William Jones proposed in 1706 the Greek letter π, based on perimetros [περίμετρος], Greek for perimeter. Leonhard Euler firmly established π in his mathematical writings.]
- Borwein, Jonathan; Borwein, Peter (1987). Pi and the AGM: a Study in Analytic Number Theory and Computational Complexity. Wiley. ISBN 978-0-471-31515-5.
- Boyer, Carl B.; Merzbach, Uta C. (1991). A History of Mathematics (2 ed.). Wiley. ISBN 978-0-471-54397-8.
- Bronshteĭn, Ilia; Semendiaev, K.A. (1971). A Guide Book to Mathematics. Verlag Harri Deutsch. ISBN 978-3-87144-095-3.
- Eymard, Pierre; Lafon, Jean Pierre (1999). The Number Pi. American Mathematical Society. ISBN 978-0-8218-3246-2., English translation by Stephen Wilson.
- Gupta, R.C. (1992). "On the remainder term in the Madhava–Leibniz's series". Ganita Bharati. 14 (1–4): 68–71.
- Howe, Roger (1980), "On the role of the Heisenberg group in harmonic analysis", Bulletin of the American Mathematical Society, 3 (2): 821–844, doi:10.1090/S0273-0979-1980-14825-9, MR 0578375.
- Joseph, George Gheverghese (1991). The Crest of the Peacock: Non-European Roots of Mathematics. Princeton University Press. ISBN 978-0-691-13526-7. Retrieved 5 June 2013.
- Posamentier, Alfred S.; Lehmann, Ingmar (2004). Pi: A Biography of the World's Most Mysterious Number. Prometheus Books. ISBN 978-1-59102-200-8.
- Reitwiesner, George (1950). "An ENIAC Determination of pi and e to 2000 Decimal Places". Mathematical Tables and Other Aids to Computation. 4 (29): 11–15. doi:10.2307/2002695. JSTOR 2002695.
- Remmert, Reinhold (2012). "Ch. 5 What is π?". In Heinz-Dieter Ebbinghaus; Hans Hermes; Friedrich Hirzebruch; Max Koecher; Klaus Mainzer; Jürgen Neukirch; Alexander Prestel; Reinhold Remmert. Numbers. Springer. ISBN 978-1-4612-1005-4.
- Rossi, Corinna (2004). Architecture and Mathematics in Ancient Egypt. Cambridge: University Press. ISBN 978-1-107-32051-2.
- Roy, Ranjan (1990). "The Discovery of the Series Formula for pi by Leibniz, Gregory, and Nilakantha". Mathematics Magazine. 63 (5): 291–306. doi:10.2307/2690896. JSTOR 2690896.
- Schepler, H.C. (1950). "The Chronology of Pi". Mathematics Magazine. 23 (3): 165–170 (Jan/Feb), 216–228 (Mar/Apr), and 279–283 (May/Jun). doi:10.2307/3029284. JSTOR 3029284.. issue 3 Jan/Feb, issue 4 Mar/Apr, issue 5 May/Jun
- Thompson, William (1894), "Isoperimetrical problems", Nature Series: Popular Lectures and Addresses, II: 571–592
برای مطالعه بیشتر
- Blatner, David (1999). The Joy of Pi. Walker & Company. ISBN 978-0-8027-7562-7.
- Borwein, Jonathan; Borwein, Peter (1984). "The Arithmetic-Geometric Mean and Fast Computation of Elementary Functions" (PDF). SIAM Review. 26 (3): 351–365. CiteSeerX 10.1.1.218.8260. doi:10.1137/1026073.
- Borwein, Jonathan; Borwein, Peter; Bailey, David H. (1989). "Ramanujan, Modular Equations, and Approximations to Pi or How to Compute One Billion Digits of Pi". The American Mathematical Monthly (Submitted manuscript). 96 (3): 201–219. doi:10.2307/2325206. JSTOR 2325206.
- Chudnovsky, David V. and Chudnovsky, Gregory V., "Approximations and Complex Multiplication According to Ramanujan", in Ramanujan Revisited (G.E. Andrews et al. Eds), Academic Press, 1988, pp. 375–396, 468–472
- Cox, David A. (1984). "The Arithmetic-Geometric Mean of Gauss". L'Enseignement Mathématique. 30: 275–330.
- Delahaye, Jean-Paul (1997). Le Fascinant Nombre Pi. Paris: Bibliothèque Pour la Science. ISBN 2-902918-25-9.
- Engels, Hermann (1977). "Quadrature of the Circle in Ancient Egypt". Historia Mathematica. 4 (2): 137–140. doi:10.1016/0315-0860(77)90104-5.
- Euler, Leonhard, "On the Use of the Discovered Fractions to Sum Infinite Series", in Introduction to Analysis of the Infinite. Book I, translated from the Latin by J.D. Blanton, Springer-Verlag, 1964, pp. 137–153
- Hardy, G. H.; Wright, E. M. (2000). An Introduction to the Theory of Numbers (fifth ed.). Oxford, UK: Clarendon Press.
- Heath, T.L., The Works of Archimedes, Cambridge, 1897; reprinted in The Works of Archimedes with The Method of Archimedes, Dover, 1953, pp. 91–98
- Huygens, Christiaan, "De Circuli Magnitudine Inventa", Christiani Hugenii Opera Varia I, Leiden 1724, pp. 384–388
- Lay-Yong, Lam; Tian-Se, Ang (1986). "Circle Measurements in Ancient China". Historia Mathematica. 13 (4): 325–340. doi:10.1016/0315-0860(86)90055-8.
- Lindemann, Ferdinand (1882). "Ueber die Zahl pi". Mathematische Annalen. 20 (2): 213–225. doi:10.1007/bf01446522. S2CID 120469397. Archived from the original on 22 January 2015.
- Matar, K. Mukunda; Rajagonal, C. (1944). "On the Hindu Quadrature of the Circle" (Appendix by K. Balagangadharan)". Journal of the Bombay Branch of the Royal Asiatic Society. 20: 77–82.
- Niven, Ivan (July 1947). "A Simple Proof that pi Is Irrational". Bulletin of the American Mathematical Society. 53 (7): 507. doi:10.1090/S0002-9904-1947-08821-2.
- Ramanujan, Srinivasa (1914). "Modular Equations and Approximations to π". Quarterly Journal of Pure and Applied Mathematics. XLV: 350–372. Reprinted in Ramanujan, Srinivasa (2015) [1927]. Hardy, G. H.; Seshu Aiyar, P. V.; Wilson, B. M., eds. Srinivasa Ramanujan: Collected Papers. Cambridge University Press. pp. 23–29. ISBN 978-1-107-53651-7.
- Shanks, William, Contributions to Mathematics Comprising Chiefly of the Rectification of the Circle to 607 Places of Decimals, 1853, pp. i–xvi, 10
- Shanks, Daniel; Wrench, John William (1962). "Calculation of pi to 100,000 Decimals". Mathematics of Computation. 16 (77): 76–99. doi:10.1090/s0025-5718-1962-0136051-9.
- Tropfke, Johannes (1906). Geschichte Der Elementar-Mathematik in Systematischer Darstellung [The history of elementary mathematics] (به آلمانی). Leipzig: Verlag Von Veit.
- Viete, Francois, Variorum de Rebus Mathematicis Reponsorum Liber VII. F. Viete, Opera Mathematica (reprint), Georg Olms Verlag, 1970, pp. 398–401, 436–446
- Wagon, Stan (1985). "Is Pi Normal?". The Mathematical Intelligencer. 7 (3): 65–67. doi:10.1007/BF03025811. S2CID 189884448.
- Wallis, John (1655–1656). Arithmetica Infinitorum, sive Nova Methodus Inquirendi in Curvilineorum Quadratum, aliaque difficiliora Matheseos Problemata (به لاتین). Oxford. Reprinted in Opera Mathematica. 1. Oxford: E Theatro Sheldoniano. 1695. pp. 357–478.
- Zebrowski, Ernest (1999). A History of the Circle: Mathematical Reasoning and the Physical Universe. Rutgers University Press. ISBN 978-0-8135-2898-4.
پیوند به بیرون
- 10 million decimal places
- "Pi" at Wolfram Mathworld
- Representations of Pi at Wolfram Alpha
- Demonstration by Lambert (1761) of irrationality of , online and analysed BibNum (PDF).
- Search Engine 2 billion searchable digits of , e and √2

