توان (ریاضی)
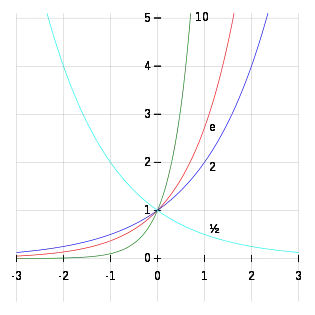
توان یک عملیات ریاضی است که به صورت نوشته میشود. این عملیات به صورت به توان خوانده میشود و در آن بهعنوان پایه و به عنوان توان، نما یا قوه شناخته میشوند. هنگامی که یک عدد صحیح مثبت باشد، عملیات توان معادل بار ضرب در خود است:
به این ترتیب و برای هر دو عدد صحیح مثبت و میتوان نوشت . همچنین با بسط تعریف عملیات به توانهای صحیح غیرمثبت، معادل تعریف میشود و ( مثبت و غیر صفر) معادل خواهد بود. به طور خاص معادل یا وارون ضربی است.
با گسترش تعریف توان، میتوان هر عدد حقیقی یا مختلط را به عنوان نما استفاده کرد. همچنین توانهای صحیح را میتوان به ساختارهای دیگر جبری (برای مثال ماتریسها) اعمال کرد.
عملیات توان در بسیاری از علوم دیگر از جمله در اقتصاد، زیستشناسی، شیمی، فیزیک و علوم رایانه و بار کاربردهایی مانند بهره مرکب، رشد جمعیت، سینتیک شیمیایی، رفتار موجی و رمزنگاری کلید عمومی مورد استفاده قرار میگیرد.
مربع یک عدد مثل x اشاره دارد به عددی مانند y که y=x² و در آن توان ایکس برابر دو است. مکعب یک عدد مثل x اشاره دارد به عددی مانند y که y=x³ و در آن توان ایکس برابر سه است.
توان با نماهای صحیح
عمل توان با نماهای صحیح تنها نیازمند جبر پایهاست.
نماهای صحیح مثبت
سادهترین نوع توان، با نماهای صحیح مثبت است. نما بیانگر این است که پایه چند بار باید در خود ضرب شود. برای مثال سه به توان پنج = ۳ × ۳ × ۳ × ۳ × ۳ = ۲۴۳. در اینجا ۳ پایه و ۵ نما است، و ۲۴۳ برابر است با ۳ به توان ۵. عدد ۳، پنج بار در خودش ضرب میشود چون نما برابر ۵ است.
به طور قراردادی، a2 = a×a را مربع، a3 = a×a×a را مکعب مینامیم. مثلا 32 «مربع سه» و 33 «مکعب سه» خوانده میشوند.
اولین توان را میتوانیم به صورت a0 = ۱ و سایر توانها را به صورت an+1 = a·an بنویسیم.
نماهای صفر و یک
35 را میتوان به صورت ۳ × ۳ × ۳ × ۳ × ۳ هم نوشت، عدد یک را میتوان چندین بار در عبارت مورد نظر ضرب کرد، زیرا در عمل ضرب عدد یک تفاوتی در جواب ایجاد نمیکند و همان جواب گذشته را میدهد. با این تعریف، میتوانیم آن را در توان صفر و یک هم استفاده کنیم:
- هر عدد به توان یک برابر خودش است.
a1 = a
- هر عدد به توان صفر برابر یک است.
a0 = 1
(برخی نویسندگان 00 را تعریف نشده میخوانند) برای مثال: a0= a2-2= a2/a2 = ۱ (در صورتی که a ≠ ۰)

نماهای صحیح منفی
اگر عددی غیرمنفی را به توان ۱- برسانیم، حاصل برابر معکوس آن عدد است.
a−1 = 1/a
در نتیجه:
a−n = (an)−1 = 1/an
اگر صفر را به توان عددی منفی برسانیم، حاصل در مخرج صفر دارد و تعریف نشدهاست. توان منفی را میتوان به صورت تقسیم مکرر پایه هم نشان داد. یعنی ۵-۳ = ۱ ÷ ۳ ÷ ۳ ÷ ۳ ÷ ۳ ÷ ۳ = ۱/۲۴۳ = 5-3/ 1.
خواص
مهمترین خاصیت توان با نماهای صحیح عبارتست از:
که از آن میتوان عبارات زیر را نتیجه گرفت:
از آنجایی که جمع و ضرب خاصیت جابجایی دارند (برای مثال ۲+۳ = ۵ = ۳+۲ و ۲×۳ = ۶ = ۳×۲) توان دارای خاصیت جابجایی نیست: 23 = ۸ است در حالی که 32 = ۹. همچنین جمع و ضرب دارای خاصیت انجمنی هستند (برای مثال (۲+۳)+۴ = ۹ = ۲+(۳+۴) و (۲×۳)×۴ = ۲۴ = ۲×(۳×۴)) توان باز هم دارای این خاصیت نیست: 23 به توان چهار برابر است با 84 یا ۴۰۹۶، در حالی که ۲ به توان 34 برابر است با 281 یا ۲٬۴۱۷٬۸۵۱٬۶۳۹٬۲۲۹٬۲۵۸٬۳۴۹٬۴۱۲٬۳۵۲. البته اعداد ۲ و ۴ در توان خاصیت جابجایی دارند چون (۱۶=۲^۴=۴^۲)
توانهای ده
در سیستم مبنای ده، محاسبه توانهای ده بسیار راحت است: برای مثال 106 برابر است با یک میلیون، که با قرار دادن ۶ صفر در جلوی یک به دست میآید. توان با نمای ده بیشتر در علم فیزیک برای نشان دادن اعداد بسیار بزرگ یا بسیار کوچک به صورت نماد علمی کاربرد دارد؛ نمونه را، ۲۹۹۷۹۲۴۵۸ (سرعت نور با یکای متر بر ثانیه) را میتوان به صورت ۲٫۹۹۷۹۲۴۵۸ × 108 نوشت و به صورت تخمینی به شکل ۲٫۹۹۸ × 108. پیشوندهای سیستم متریک هم برای نشان دادن اعداد بزرگ و کوچک استفاده میشوند و اصل اینها هم بر توان ۱۰ استوار است. نمونه را پیشوند کیلو یعنی 103 = ۱۰۰۰، پس یک کیلومتر برابر ۱۰۰۰ متر است.
توانهای عدد دو
توانهای عدد دو نقش بسیار مهمی در علم رایانه دارند چون در کامپیوتر مقادیر را میتوان برای یک متغیر هر عدد بیتی درنظر گرفت.
توانهای منفی دو هم استفاده میشوند، و به دو توان اول نصف و ربع میگویند.
توانهای عدد صفر (۰)
اگر توان صفر مثبت باشد، حاصل عبارت برابر خود صفر است:.
اگر توان صفر منفی باشد، حاصل عبارت تعریف نشدهاست، زیرا تقسیم بر صفر وجود ندارد.
اگر توان یک عدد صفر باشد، حاصل عبارت برابر یک است:.
(بعضی از نویسندگان میگویند که تعریف نشدهاست)
توانهای منفی یک
توانهای منفیِ یک بیشتر در دنبالههای تناوبی کاربرد دارد.
اگر نمای عددِ منفیِ یک، فرد باشد، حاصل آن برابر خودش است:
اگر نمای عددِ منفیِ یک، زوج باشد، حاصل آن برابر یک است:
توانهای
توانهای در دنبالههای با دورهٔ ۴ کاربرد دارند.
توانهایEعدد eEحد دنبالهای با توان صحیح است
.
و تقریباً داریم:
.
یک توان صحیح غیر صفر e برابر است با:
x میتواند عددی مانند صفر، کسر، عدد مرکب، یا یک ماتریس مربع باشد.
توانهای اعداد حقیقی مثبت
به توان رساندن عددی حقیقی مثبت به توان یک عدد غیرصحیح را میتوان به چند صورت به دست آورد:
- عددی کسری تعریف کنیم و ریشه nام را به دست بیاوریم. این روشی است که در مدرسهها از آن استفاده میکنند.
- لگاریتم طبیعی تعریف کنیم و سطح زیر نمودار 1/x را به دست بیاوریم.
توانهای کسری
در یک توان، با معکوس کردن نما ریشه آن بدست میآید. اگر عدد حقیقی مثبت و n عددی صحیح مثبتی باشد، داریم:
و ریشه nام نامیده میشود:
برای مثال: 81/3 = ۲. حالا میتوانیم توان را به صورت زیر تعریف کنیم:
aبه توان n/m مساوی است با ریشه ی a بافرجهm به توان
برای مثال: 82/3 = ۴.
توانهای مرکب اعداد مرکب
خلاصه
توانهای صحیح اعداد مرکب به صورت بازگستی تعریف میشود:
z0 = 1 zn+1 = z·zn z−n = 1/zn (برای z ≠ 0)
توانهای مرکب عدد e به صورت زیر تعریف میشود:
و توان مرکب یک عدد مرکب برابر است با:
az = ebz
اگر:
a = eb
معادله لگاریتم
عدد حقیقی مثبت π وجود دارد که با استفاده از آن میتوان معادله ez = ۱ را به صورت z = ۲πi·n حل نمود.
حالت قطبی
هر عدد مرکب به شکل را میتوان به این صورت نوشت:
برای یک مقدار حقیقی مثبت و یک کمان میتوانیم از فرمول اویلر برای استفاده کنیم:
حال میتوانیم یک بار دیگر از فرمول اویلر استفاده کنیم، در این صورت به جای e مینویسیم: . در نتیجه داریم:
حال اگر از استفاده کنیم میتوانیم بنویسیم:
مثال
این مقدار اصلی اما میتوانیم برای هر عدد صحیح n آن را به صورت بنویسیم، که نتیجه به صورت زیر است:
جدول توان
جدول kn، k در سمت چپ و n در بالای جدول است.
| n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| k^ | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1.024 | 2 | |
| 3 | 3 | 9 | 27 | 81 | 243 | 729 | 2.187 | 6.561 | 19.683 | 59.049 | 3 | |
| 4 | 4 | 16 | 64 | 256 | 1.024 | 4.096 | 16.384 | 65.536 | 262.144 | 1.048.576 | 4 | |
| 5 | 5 | 25 | 125 | 625 | 3.125 | 15.625 | 78.125 | 78.125 | 1.953.125 | 9.765.625 | 5 | |
| 6 | 6 | 36 | 216 | 1.296 | 7.776 | 46.656 | 279.936 | 1.679.616 | 10.077.696 | 60.466.176 | 6 | |
| 7 | 7 | 49 | 343 | 2.401 | 16.807 | 117.649 | 823.543 | 5.764.801 | 40.353.607 | 282.475.249 | 7 | |
| 8 | 8 | 64 | 512 | 4.096 | 32.768 | 262.144 | 2.097.152 | 16.777.216 | 134.217.728 | 1.073.741.824 | 8 | |
| 9 | 9 | 81 | 729 | 6.561 | 59.049 | 531.441 | 4.782.969 | 43.046.721 | 387.420.489 | 3.486.784.401 | 9 | |
| 10 | 10 | 100 | 1.000 | 10.000 | 100.000 | 1.000.000 | 10.000.000 | 100.000.000 | 1.000.000.000 | 10.000.000.000 | 10 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| n | ||||||||||||
ضرب اعداد توان دار
2 حالت ممکن است برای ضرب اعداد توان دار رخ دهد:
- پایهها برابر
- توانها برابر
پایهها برابر
برای اینکار یکی از پایهها را نوشته و توانها را جمع میکنیم:
توانها برابر
برای اینکار یکی از توانها را نوشته و پایهها را در هم ضرب میکنیم.
تقسیم اعداد توان دار
2 حالت ممکن است برای تقسیم اعداد توان دار رخ دهد:
- پایهها برابر
- توانها برابر
پایهها برابر
برای اینکار یکی از پایهها را نوشته و توانها را کم میکنیم:
توانها برابر
برای اینکار یکی از توانها را نوشته و پایهها را بر هم تقسیم میکنیم.
جذر گرفتن از اعداد تواندار
برای محاسبه جذر اعداد تواندار مثل کافی است توان را بر فرجه تقسیم کنیم.
پانوشت
مبحث ضرب اعداد تواندار «سیده فاطمه موسوی نطنزی»
پیوند به بیرون
| در ویکیانبار پروندههایی دربارهٔ توان (ریاضی) موجود است. |
| عملیات دوتایی | ||||
|---|---|---|---|---|
| عددی | تابعی | مجموعهای | ساختاری | |
|
مقدماتی
+ جمع حسابی
div خارج قسمت اقلیدسی ترکیباتی
() ضریب دوجملهای |
∘ ترکیب ∗ کانولوشن |
جبر مجموعهها
∪ اجتماع ترتیب کلی
min کمینه توریها
|
مجموعهها
× ضرب دکارتی گروهها
⊕ حاصلجمع مستقیم مدولها
⊗ ضرب تانسوری |
درختها
∨ enracinement واریتههای متصل
# جمع متصل فضاهای نقطهدار
∨ bouquet |
| بُرداری | ||||
| (.) ضرب اسکالر ∧ ضرب برداری | ||||
| جبری | ||||
| [,] کروشه لی {,} کروشه پواسون ∧ ضرب خارجی | ||||
| هومولوژی | ||||
| ∪ cup-produit • حاصلضرب اشتراک |
ترتیبی | |||
| + الحاق | ||||
| منطق بولی | ||||
| ∧ عطف منطقی | ∨ فصل منطقی | ⊕ یای انحصاری | ⇒ استلزام منطقی | ⇔ اگر و فقط اگر |
