تابع یکبهیک
فرض کنید f:X→Y یک تابع باشد. در اینصورت برای تناظری که بین اعضای X و Y بهوسیله تابع f برقرار میشود حالات مختلفی را میتوان تصور کرد.
| تابع | |||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x ↦ f (x) | |||||||||||||||||||||||||||||||||
| مثالهایی با دامنه و دامنه مشترک | |||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| کلاسها/ویژگیها | |||||||||||||||||||||||||||||||||
| ثابت · همانی · خطی · چندجملهای · گویا · جبری · تحلیلی · هموار · پیوسته · قابل اندازهگیری · یکبهیک · پوشا · دوسویی | |||||||||||||||||||||||||||||||||
| سازههای تابعی | |||||||||||||||||||||||||||||||||
| محدود سازی · ترکیب · لاندا · وارون | |||||||||||||||||||||||||||||||||
| تعمیم تابع | |||||||||||||||||||||||||||||||||
| جزئی · چندمقداری · ضمنی | |||||||||||||||||||||||||||||||||
اولین حالت اینکه ممکن است به ازای هر y متعلق به برد تابع f، تنها یک x در دامنه موجود باشد که (y=f(x. این شرط را میتوان چنین فرمول بندی کرد که اگر به ازای x1,x2∈X داشته باشیم (f(x1)=f(x2 آنگاه x1=x2 یا:
چنین تابعی را با این ویژگی یک تابع یک به یک (تک گزین) یا انژکتیو میگوییم.[1] یک به یک بودن تابع f را گاهی برای اختصار با نماد ۱–۱ نشان میدهند. در چنین حالتی ضمن اینکه به دلیل تابع بودن f هیچ دو زوج مرتبی از f دارای مؤلفه اول یکسان نمیباشند، به دلیل یک به یک بودن هیچ دو زوج مرتبی از f دارای مؤلفه دوم یکسان نیز نمیباشند.
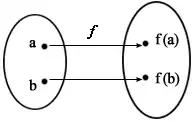
یک به یک بودن یک تابع از روی نمودار تابع نیز قابل بررسی است. در نمودار پیکانی تابع یک به یک f، وضوحاً به هر عضو از همدامنه f انتهای حداکثر یک پیکان وارد شدهاست. به این ترتیب نمودار پیکانی شکل(۲) نمایش گر یک تابع غیر یک به یک است. همچنین نمودار یک تابع حقیقی یک به یک به گونهای است که هر خط موازی محور xها، نمودار آن را حداکثر در یک نقطه قطع میکند. به این ترتیب نمودار شکل(۴) مربوط به تابعی غیر یک به یک است.
f: R ---> R f(x) = |x| + x
x1 = -2 ---> f(x1) = |-۲| + (-۲) = ۰ x2 = -3 ---> f(x2) = |-۳| + (-۳) = ۰ x2 ≠ x1 ---> f(x1) = f(x2)
F یک به یک نیست (۱)
منابع
- توماس، جورج ب. حساب دیفرانسیل و انتگرال و هندسهٔ تحلیلی. نیاز دانش. صص. ۷۴.
