دنباله
در ریاضیات، یک دنباله (به انگلیسی: Sequence) یک گردآوری شمارا از اشیاء است که در آن تکرار مجاز و ترتیب مهم است[1].
مشابه یک مجموعه، دنباله شامل چند عضو (یا جمله) است. تعداد اعضای یک دنباله (شاید نامتناهی) «طول دنباله» نامیده میشود. برخلاف یک مجموعه، در یک دنباله، عناصر مشابه میتوانند چندین بار در محلهای مختلف یک دنباله پدیدار شوند و ترتیب آنها اهمیت دارد.
به عنوان مثال، یک دنباله است که به ترتیب از ۵ و ۳ و ۳ و ۸ تشکیل شده و با یا یکسان نیست.
به مکانی که یک عضو در یک دنباله قرار دارد «اندیس»ِ آن عضو میگویند[1]، به عنوان مثال ۸، چهارمین عضو دنبالهٔ فوق است پس اندیس آن، ۴ است. اندیس اوّلین عضو دنباله را معمولاً ۱ تعریف میکنند. nـُمین عضو یک دنباله مانند را به صورت نمایش میدهند.
به دنبالهای به طول ، یک n-تایی مرتّب (tuple) نیز گفته میشود[2].
در نظریّهٔ تحلیلی اعداد، به دنبالهای که اعضای آن حقیقی یا مختلط باشند تابع حسابی یا دنبالهٔ حقیقی میگویند. در علوم رایانه، رشته دنبالهای از نویسهها است.
تعریف و نمایش
در بیشتر منابع، اندیسهای دنباله باید شامل تمام اعداد طبیعی باشند (دنباله نامتناهی باشد)[3] یا این که میتوانند اعداد طبیعی کوچکتر از باشد (دنباله متناهی باشد)؛ امّا در بعضی موارد (بر اساس نیاز) این تعریف تعمیم داده میشود. به این صورت که اندیسها میتوانند هر بازهای از اعداد صحیح باشد[1].
تعریف دقیق دنباله
در نظریّهٔ مجموعهها، دنباله به صورت تابعی تعریف میشود که دامنهٔ آن اعداد طبیعی باشد[3]:
نمایش
برای نمایش دنبالهها از استفاده میشود. برای دنبالههای متناهی از پرانتز نیز استفاده میشود. مثال:
معمولاً برای جلوگیری از کژتابی، جملهٔ عمومی نیز نوشته میشود:
در بسیاری از منابع، به جای از استفاده میشود[4] امّا در این مقاله برای اشتباه نشدن با مجموعهها، از این نمادها استفاده نشده. در بعضی منابع نیز از استفاده از نمادها پرهیز شده است[3].
نمایش با جملهٔ عمومی
به ضابطهٔ یک دنباله مانند ، «جملهٔ عمومی» آن میگویند. مثال:
گاهی (با این که این نمایش معمولاً برای دنبالههای نامتناهی استفاده میشود)، حدود اندیسها را نیز مشخّص میکنند[1][4]:
نمایش بازگشتی
در این روش، مقدار هر جمله از دنباله وابسته به جملات قبلی آن است[1]. مثل دنبالهٔ فیبوناچی:
بعضی مواقع میتوان دنبالهٔ بازگشتی را ساده کرد و نمایش جملهٔ عمومی آن را پیدا کرد. به عنوان مثال دنبالهٔ
را میتوان به صورت ساده کرد.
تابع آکرمن مثالی ست از مواقعی که نمیتوان دنباله را ساده کرد:
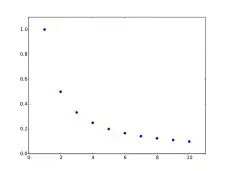
نمایش نموداری
دنبالهها نیز مانند بقیهٔ توابع میتوانند به صورت نموداری نمایش داده شوند. مثال:
ویژگیها
یکنوایی دنبالهها
از آن جایی که دنباله نوعی تابع است، تعریف یکنوایی توابع در این مورد نیز همان است.
شرط یکنوایی
این قضیه بیان میدارد که یک دنباله صعودی ست اگر و تنها اگر هر جملهٔ آن از جملهٔ قبلی بزرگتر باشد[3]:
و نزولی نیز به صورت مشابه:
شرط اکیداً صعودی و اکیداً نزولی نیز به شکل مشابه.
دنبالههای خاص
تصاعد حسابی
در این نوع از دنبالهها، اختلاف هر جمله با جملهٔ پیشین مقداری ثابت است.
تصاعد هندسی
در این نوع از دنبالهها، نسبت هر جمله به جملهٔ پیشین مقداری ثابت است.
دنبالهٔ چندجملهای
دنبالهٔ چندجملهای دنبالهای ست که هر جملهٔ آن ضریب تابعی چندجملهای باشد. مثال:
دنبالهٔ دنبالهٔ چندجملهای است.
.png.webp)
مجموع جزئی
برای یک دنباله مانند ، دنبالهٔ مجموع جزئی متناظر با آن به صورت زیر تعریف میشود[6]:
عنصر nـُم سری فوق را «جمع جزئی»ِ n عضو اوّل دنباله میگویند.
حد مجموع جزئی در بینهایت همان سری دنباله است
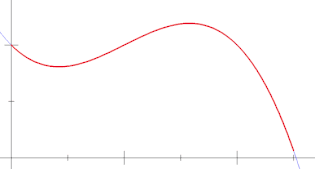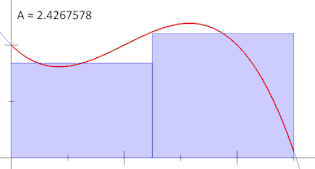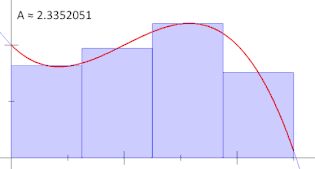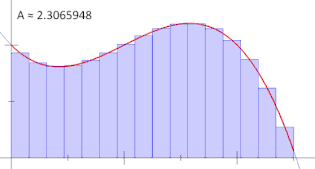
مفهوم جمع جزئی شباهت بسیاری با انتگرال دارد. در واقع، انتگرالِ یک تابع به کمک حد این جمع تعریف میشود.
حد و همگرایی
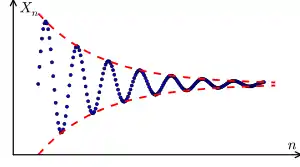
از آنجا که دنباله یک تابع گسسته میباشد، باید حد آن در بینهایت را اختصاصاً تعریف کرد.
اگر چنین مقداری وجود داشته باشد، دنباله را «همگرا» میگوییم و به اصطلاح، دنباله به آن مقدار میل میکند.
به عنوان مثال دنبالهٔ به صفر میل میکند:

در غیر این صورت دنباله را «واگرا» میگوییم. یک دنبالهٔ واگرا میتواند به ∞ یا -∞ میل کند یا به هیچ مقداری میل نکند.
به عنوان مثال دنبالهٔ به هیچ مقداری میل نمیکند:
و دنبالهٔ به ∞ میل میکند:
گاهی حد دنبالهای مانند را به صورت (با حروف بزرگ) نمایش میدهند:
سری
با وجود این که کلمات «سری» و «دنباله» عموماً مترادف یکدیگر هستند، در ریاضیات مفاهیم متفاوتی دارند.
سری متناظر با یک دنباله به صورت نمایش داده میشود و یافتن مقدار سری از اهمّیّت بالایی برخوردار است.
جمع اعضای یک دنبالهٔ واگرا تعریف نشده است. به عبارت دقیقتر، سری واگرا ست.
از معروفترین مثالهای این حالت میتوان به سری گرندی:
و این سری اشاره کرد:
جمع اعضای یک دنبالهٔ همگرا نیز ممکن است تعریف نشده باشد.
سری همساز از مثالهای معروف این حالت است:
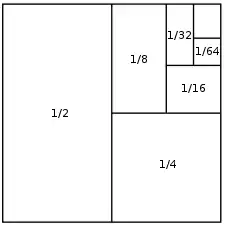
همچنین جمع اعضای یک دنبالهٔ همگرا میتواند همگرا باشد.
این سری از مثالهای معروف این حالت است:
جستارهای وابسته
- حد دنباله (و دنبالههای همگرا و واگرا)
- دنباله فیبوناچی
- دانشنامه برخط دنبالههای صحیح
- عدد مثلثی
- مربّع کامل
- نظریه نامتغیر
منابع
- "Sequence". Wikipedia. 2021-01-17.
- "Tuple". Wikipedia. 2021-01-06.
- «فصل ۱۰». حسابان (اپوستول) Calculus Vol. 1 (2nd ed.) (Tom M. Apostol). شابک ۹۷۸-۰-۴۷۱-۰۰۰۰۵-۱.
- «فصل ۱۰». حسابان توماس Thomas' Calculus (14th Edition). شابک ۹۷۸-۰۱۳۴۴۳۸۹۸۶.
- «دنبالهٔ کراندار» [ریاضی] همارزِ «bounded sequence»؛ منبع: گروه واژهگزینی. جواد میرشکاری، ویراستار. دفتر سوم. فرهنگ واژههای مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۶۴-۷۵۳۱-۵۰-۸ (ذیل سرواژهٔ دنبالهٔ کراندار)
- «فصل ۱۰». حسابان (اپوستول) Calculus Vol. 1 (2nd ed.) (Tom M. Apostol). شابک ۹۷۸-۰-۴۷۱-۰۰۰۰۵-۱.
- ریچارد سیلورمن (۱۳۸۵)، حساب دیفرانسیل و انتگرال و هندسه تحلیلی جدید (جلد اول)، ترجمهٔ دکتر علی اکبر عالم زاده، تهران: انتشارات علمی فنی، شابک ۹۶۴-۶۲۱۵-۰۶-۸
