قاعده کرامر

در جبر خطی، قاعده کرامر روشی صریحی برای حل دستگاه معادلات خطی ای که تعداد معادلات با تعداد مجهولات برابر و دستگاه جواب منحصر بفرد دارد، است. این روش از دترمینان‌های ماتریس (مربع) ضرایب و ماتریس‌هایی که از جایگزینی یکی از ستون‌های ماتریس ضرایب با بردار سمت راست معادله بدست می‌آید، تعریف می‌گردد. این روش به نام گابریل کرامر (۱۷۰۴–۱۷۵۲) که این روش را برای تعداد دلخواهی از مجهولات در سال ۱۷۵۰ منتشر کرد[1]. اگرچه کولین مک‌لورین نیز در سال ۱۷۴۸ برای موارد خاص این روش را منتشر کرده بود[2] (و احتمالاً در ۱۷۲۹ نیز این روش شناخته شده بود).[3][4][5]

حالت کلی

دستگاهی با n معادله و n مجهول را نظر بگیرید، که بشکل ماتریسی زیر قابل نمایش است:

Ax=b\,

(1)\,

که در آن ماتریس $A$ ، n در n و دترمینانش مخالف صفر و بردار $x=(x_{1},\ldots ,x_{n})^{\mathrm {T} }$ بردار ستونی متغیرها است.

قضیه بیان می‌کند که در این حالت معادله جواب منحصر بفردی دارد، که مقدار متغیرهایش از رابطه زیر بدست می‌آید:

x_{i}={\frac {\det(A_{i})}{\det(A)}}\qquad i=1,\ldots ,n\,

که در آن $A_{i}$ ماتریس حاصل از جایگذاری بردار ستونی $b$ در ستون $i$ ام $A$ می‌باشد.

قاعده کرامر برای معادلات با ضرایب و مجهولات تنها برایاعداد حقیقی نیست و برای هرمیدان تعریف می‌گردد. اخیراً نشان داده شده‌است که قاعده کرامر را می‌توان در زمان $O(n^{3})$ پیاده‌سازی کرد،[6] که قابل مقایسه با سایر روش‌های رایج برای حل دستگاه معادلات خطی مانند روش حذفی گاوسی می‌باشد.

اثبات

می‌دانیم که $\det(A)\neq 0$ پس بنا به خواص دترمینان، ماتریس A معکوس دارد. از معکوس داشتن A نتیجه می‌گیریم که معادله $Ax=b$ جواب منحصر بفرد $A^{-1}b$ را دارد. $(A(A^{-1}b)=(AA^{-1})b=b)$

برای هر عدد صحیح $i,1\leq i\leq n$ $a_{i}$ را ستون iام ماتریس $A$ و $e_{i}$ را ستون i ام ماتریس همانی $I_{n}$ در نظر بگیرید و $X_{i}$ را ماریسی که از جایگذاری بردار ستونی $x$ در ستون iام ماتریس همانی بدست می‌آید، در نظر بگیرید.

می‌دانیم ستون kام حاصل ضرب $AB$ برای هر ماتریس $A,B$ ، از ضرب ماتریس $A$ در ستون kام ماتریس $B$ بدست می‌آید. پس به‌طور مشابه بدست می‌آید $Ae_{k}=a_{k}$ بازای $k=1,\ldots ,n$ . بنابراین خواهیم داشت:

${\begin{array}{lll}AX_{i}&=&A(e_{1},\ldots ,e_{i-1},x,e_{i+1},\ldots ,e_{n})\\&=&(Ae_{1},\ldots ,Ae_{i-1},Ax,Ae_{i+1},\ldots ,Ae_{n})\\&=&(a_{1},\ldots ,a_{i-1},b,a_{i+1},\ldots ,a_{n})\\&=&A_{i}\end{array}}$

می‌دانیم $X_{i}$ برابر $I_{n}$ ای که ستون iامش با بردار ستونی x تعویض شده‌است، می‌باشد. دترمینان ماتریس $X_{i}$ را بدست می‌آوریم:

$\det(X_{i})=(-1)^{i+i}x_{i}\det(I_{n-1})=1.x_{i}.1=x_{i}$

سپس دترمینان ماتریس حاصل ضرب را بدست می‌آوریم:

$\det(A_{i})=\det(AX_{i})=\det(A)\det(X_{i})=det(A)x_{i}$

که از اینجا خواهیم داشت:

$x_{i}={\frac {\det(A_{i})}{\det(A)}}$

یافتن ماتریس معکوس

ابتدا ماتریس A, n×n را در نظر می‌گیریم

\mathrm {Adj} (A)A=\mathrm {det} (A)I\,

(Adj(A ماتریس الحاقی ماتریس A است و (det(A قابل محاسبه است و I ماتریس همانی است. اگر دترمینان A در R مخالف صفر باشد، آنگاه معکوس ماتریس A برابر است با:

A^{-1}={\frac {1}{\operatorname {det} (A)}}\operatorname {Adj} (A)

اگر R یک میدان باشد (مثل میدان اعداد حقیقی) در صورتی که det(A)≠۰ فرمولی برای محاسبه ماتریس معکوس بدست می‌آید. به شرطی که (det(A یکتا باشداین فرمول برای هر زمانی که R یک حلقه جابه جایی باشد برقرار است. اگر (det(A یکتا نباشد آنگاه A ماتریس معکوس ندارد.

کاربردها

فرمول صریح برای دستگاه‌های کوچک

دستگاه خطی $\left\{{\begin{matrix}ax+by&={\color {red}e}\\cx+dy&={\color {red}f}\end{matrix}}\right.\$ را در نظر می‌گیریم که قالب ماتریسی آن به صورت ${\begin{bmatrix}a&b\\c&d\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}{\color {red}e}\\{\color {red}f}\end{bmatrix}}.$ است. فرض می‌کنیم ad-bc≠۰ باشد.

سپس xو y را با قاعده کرامر میابیم:

$x={\begin{vmatrix}\color {red}{e}&b\\\color {red}{f}&d\end{vmatrix}}/{\begin{vmatrix}a&b\\c&d\end{vmatrix}}={{\color {red}e}d-b{\color {red}f} \over ad-bc}\quad ,\quad y={\begin{vmatrix}a&\color {red}{e}\\c&\color {red}{f}\end{vmatrix}}/{\begin{vmatrix}a&b\\c&d\end{vmatrix}}={a{\color {red}f}-{\color {red}e}c \over ad-bc}$

این قانون در ماتریس‌های ۳×۳ مشابه است.دستگاه $\left\{{\begin{matrix}ax+by+cz&={\color {red}j}\\dx+ey+fz&={\color {red}k}\\gx+hy+iz&={\color {red}l}\end{matrix}}\right.$ را در نظر بگيريد كه فرم ماتریسی آن به صورت ${\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}}{\begin{bmatrix}x\\y\\z\end{bmatrix}}={\begin{bmatrix}{\color {red}j}\\{\color {red}k}\\{\color {red}l}\end{bmatrix}}$ است

همچنین مقادیرxو y و z از روابط زیر به دست می‌آیند:

x={\frac {\begin{vmatrix}{\color {red}j}&b&c\\{\color {red}k}&e&f\\{\color {red}l}&h&i\end{vmatrix}}{\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}}\quad ,\quad y={\frac {\begin{vmatrix}a&{\color {red}j}&c\\d&{\color {red}k}&f\\g&{\color {red}l}&i\end{vmatrix}}{\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}}\quad ,\quad z={\frac {\begin{vmatrix}a&b&{\color {red}j}\\d&e&{\color {red}k}\\g&h&{\color {red}l}\end{vmatrix}}{\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}}

هندسه دیفرانسیل

قاعده کرامر برای حل مسائل هندسه دیفرانسیل بسیار مفید است. دو معادله $F(x,y,u,v)=0\,$ و $G(x,y,u,v)=0\,$ را در نظر می‌گیریم. زمانی که u و v دو متغیر مستقل باشند، x را $x=X(u,v)\,$ و y را $y=Y(u,v)\,$ تعریف می‌کنیم. پیدا کردن یک معادله برای ${\dfrac {\partial x}{\partial u}}$ یک برنامه بدیهی قاعده کرامر است. ابتدا مشتقات F و G و x و y را محاسبه می‌کنیم.

dF={\frac {\partial F}{\partial x}}dx+{\frac {\partial F}{\partial y}}dy+{\frac {\partial F}{\partial u}}du+{\frac {\partial F}{\partial v}}dv=0

dG={\frac {\partial G}{\partial x}}dx+{\frac {\partial G}{\partial y}}dy+{\frac {\partial G}{\partial u}}du+{\frac {\partial G}{\partial v}}dv=0

dx={\frac {\partial X}{\partial u}}du+{\frac {\partial X}{\partial v}}dv

dy={\frac {\partial Y}{\partial u}}du+{\frac {\partial Y}{\partial v}}dv

dx و dy را در df وdg جایگزین می‌کنیم و به روابط زیر می‌رسیم:

dF=\left({\frac {\partial F}{\partial x}}{\frac {\partial x}{\partial u}}+{\frac {\partial F}{\partial y}}{\frac {\partial y}{\partial u}}+{\frac {\partial F}{\partial u}}\right)du+\left({\frac {\partial F}{\partial x}}{\frac {\partial x}{\partial v}}+{\frac {\partial F}{\partial y}}{\frac {\partial y}{\partial v}}+{\frac {\partial F}{\partial v}}\right)dv=0

dG=\left({\frac {\partial G}{\partial x}}{\frac {\partial x}{\partial u}}+{\frac {\partial G}{\partial y}}{\frac {\partial y}{\partial u}}+{\frac {\partial G}{\partial u}}\right)du+\left({\frac {\partial G}{\partial x}}{\frac {\partial x}{\partial v}}+{\frac {\partial G}{\partial y}}{\frac {\partial y}{\partial v}}+{\frac {\partial G}{\partial v}}\right)dv=0

تا زمانی که u و v دو متغیر مستقل باشند، ضرایب du و dv حتماً باید صفر باشد. سپس ما می‌توانیم معادلات ضرایب را بنویسیم:

{\frac {\partial F}{\partial x}}{\frac {\partial x}{\partial u}}+{\frac {\partial F}{\partial y}}{\frac {\partial y}{\partial u}}=-{\frac {\partial F}{\partial u}}

{\frac {\partial G}{\partial x}}{\frac {\partial x}{\partial u}}+{\frac {\partial G}{\partial y}}{\frac {\partial y}{\partial u}}=-{\frac {\partial G}{\partial u}}

{\frac {\partial F}{\partial x}}{\frac {\partial x}{\partial v}}+{\frac {\partial F}{\partial y}}{\frac {\partial y}{\partial v}}=-{\frac {\partial F}{\partial v}}

{\frac {\partial G}{\partial x}}{\frac {\partial x}{\partial v}}+{\frac {\partial G}{\partial y}}{\frac {\partial y}{\partial v}}=-{\frac {\partial G}{\partial v}}

حالا با توجه به قاعده کرامر می‌بینیم که:

{\frac {\partial x}{\partial u}}={\frac {\begin{vmatrix}-{\frac {\partial F}{\partial u}}&{\frac {\partial F}{\partial y}}\\-{\frac {\partial G}{\partial u}}&{\frac {\partial G}{\partial y}}\end{vmatrix}}{\begin{vmatrix}{\frac {\partial F}{\partial x}}&{\frac {\partial F}{\partial y}}\\{\frac {\partial G}{\partial x}}&{\frac {\partial G}{\partial y}}\end{vmatrix}}}

که این فرمول دو جمله از ماتریس ژاکوبی است.

{\frac {\partial x}{\partial u}}=-{\frac {\left({\frac {\partial \left(F,G\right)}{\partial \left(u,y\right)}}\right)}{\left({\frac {\partial \left(F,G\right)}{\partial \left(x,y\right)}}\right)}}

همچنین این روابط را می‌توان برای ${\frac {\partial x}{\partial v}}$ ، ${\frac {\partial y}{\partial u}}$ ، ${\frac {\partial y}{\partial v}}$ به دست آورد.

معادلات دیفرانسیل معمولی

قاعده کرامر برای به دست آوردن جواب عمومی معادله دیفرانسیل خطی ناهمگن با استفاده از روش تغییر پارامترها استفاده می‌شود.

تعبیر هندسی

تعبیر هندسی قاعده کرامر. مساحت‌های متواضی الاضلاع‌های هاشور خوردهٔ دوم و سوم یکسان هستند و متوازی‌الاضلاع دوم

x_{1}

برابر اولی است. قاعده کرامر از این برابری‌ها استفاده می‌کند.

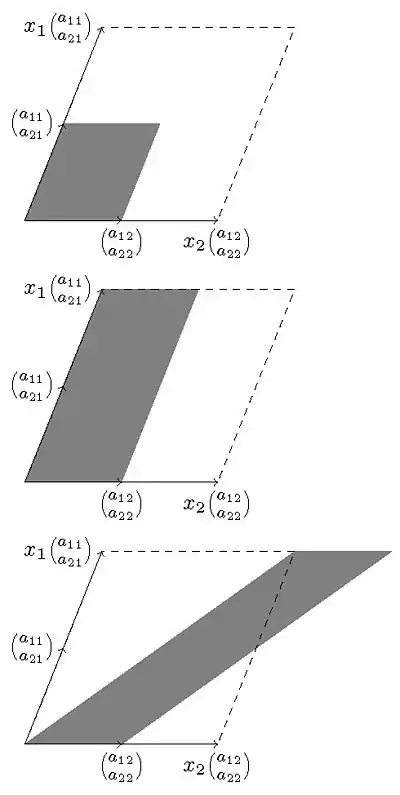
قاعده کرامر تعبیر هندسی دارد که می‌توان از آن برای اثبات یا ساده کردن تصور ماهیت هندسی قاعده کرامر استفاده کرد.

دستگاه معادلات داده شده زیر را در نظر بگیرید:

{\begin{matrix}a_{11}x_{1}+a_{12}x_{2}&=b_{1}\\a_{21}x_{1}+a_{22}x_{2}&=b_{2}\end{matrix}}

می‌توان دستگاه را به صورت معادله‌ای بین دو بردار در نظر گرفت.

x_{1}{\binom {a_{11}}{a_{21}}}+x_{2}{\binom {a_{12}}{a_{22}}}={\binom {b_{1}}{b_{2}}}.

مساحت متوازی‌الاضلاع‌هایی که از روابط ${\binom {a_{11}}{a_{21}}}$ و ${\binom {a_{12}}{a_{22}}}$ بدست می‌آیند، را می‌توان از دترمینان دستگاه معادلات بدست آورد:

$\left|{\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{matrix}}\right|.$

بصورت کلی اگر تعداد متغیرها از معادلات بیشتر باشد، دترمینان $n$ بردار از طول $n$ حجم ''متوازی السطوح'' که از آن بردارها در فضای اقلیدسی $n$ بعدی ساخته می‌شود، را محاسبه می‌کند.

بنابراین مساحت متوازی‌الاضلاع ای که از $x_{1}{\binom {a_{11}}{a_{21}}}$ و ${\binom {a_{12}}{a_{22}}}$ بدست می‌آید، باید $x_{1}$ برابر مساحت اولی باشد زیرا یکی از اضلاع آن توسط این تابع چند برابر شده‌است. حال مسحات آخرین متوازی‌الاضلاع، با استفاده از اصل کاوالیری، مساحتی برابر با متوازی‌الاضلاعی است که از ${\binom {b_{1}}{b_{2}}}=x_{1}{\binom {a_{11}}{a_{21}}}+x_{2}{\binom {a_{12}}{a_{22}}}$ و ${\binom {a_{12}}{a_{22}}}$ بدست می‌آید.

برابر کردن مساحت‌های آخرین و دومین متوازی‌الاضلاع معادله $\left|{\begin{matrix}b_{1}&a_{12}\\b_{2}&a_{22}\end{matrix}}\right|=\left|{\begin{matrix}a_{11}x_{1}&a_{12}\\a_{21}x_{1}&a_{22}\end{matrix}}\right|=x_{1}\left|{\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{matrix}}\right|$ را می‌دهد که قاعده کرامر از آن استفاده می‌کند.

اثبات کوتاه

اثباتی کوتاه برای قاعده کرامر می‌توان ارئه داد. فرض می‌کنیم $x_{1}$ دترمینان ماتریس زیر باشد.

X_{1}={\begin{bmatrix}x_{1}&0&0&\dots &0\\x_{2}&1&0&\dots &0\\x_{3}&0&1&\dots &0\\\vdots &\vdots &\vdots &\ddots &\vdots \\x_{n}&0&0&\dots &1\end{bmatrix}}

از سوی دیگر، فرض کنید ماتریس اصلی ما $A$ معکوس پذیر باشد، ماتریس $X_{1}$ ستون‌های $A^{-1}b,A^{-1}v_{2},\ldots ,A^{-1}v_{n}$ را دارد که $v_{k}$ $k$ -امین بردار ماتریس $A$ باشد. باید آورید که $A_{1}$ ستون‌های $b,v_{2},\ldots ,v_{n}$ را دارا می‌باشد؛ بنابراین ما $x_{1}=\det(X_{1})=\det(A^{-1})\det(A_{1})={\frac {\det(A_{1})}{\det(A)}}$ را خواهیم داشت که همان چیزی است که دنبالش می‌گشتیم. اثبات بقیه $x_{j}$ به‌طور مشابه می‌باشد.

موارد ناسازگار و نامعین

یک دستگاه معادله زمانی ناسازگار است که هیچ جوابی ندارد و زمانی نا مشخص است که بیش از یک جواب داشته باشد. برای معادلات خطی دستگاه نامعین بی شمار جواب خواهد داشت (اگر میدان نامحدود باشد). ار آنجاییکه جواب می‌تواند در جمله‌ای از یک یا چند پارامتر بیان شود پس می‌تواند مقادیر دلخواه بگیرد. قاعده کرامر جایی که دترمینان مخالف صفر باشد روی مورد اعمال می‌شود. در مورد مقابل دستگاه بر اساس مقدار دترمینان برای دستگاه‌های ۲×۲ یا نامعین است یا ناسازگار. برای دستگاه‌های ۳×۳ یا بالاتر باید به نکته‌ای اشاره کرد که اگر ماتریس ضریب دترمینان مساوی با صفر باشد اگر صورت کسر دترمینان مخالف صفر بود حتماً این دستگاه ناسازگار است. اگرچه این حرف اشتباه است که :دترمینان‌های مساوی صفر به اینکه دستگاه نامعین است اشاره ندارند. در مثال زیر دترمینان‌ها مساوی صفر هستند ولی دستگاه ۳×۳ هنوز نامعین است. $x+y+z=1,x+y+z=2,x+y+z=3$

جستارهای وابسته

یادداشت‌ها

Cramer, Gabriel (1750). "Introduction à l'Analyse des lignes Courbes algébriques" (به French). Geneva: Europeana. pp. 656–659. Retrieved 2012-05-18.
MacLaurin, Colin (1748). A Treatise of Algebra, in Three Parts.
Boyer, Carl B. (1968). A History of Mathematics (2nd ed.). Wiley. p. 431.
Katz, Victor (2004). A History of Mathematics (Brief ed.). Pearson Education. pp. 378–379.
Hedman, Bruce A. (1999), "An Earlier Date for "Cramer's Rule"", Historia Mathematica, 4(26): 365–368, doi:10.1006/hmat.1999.2247
Ken Habgood, Itamar Arel (2012). "A condensation-based application of Cramerʼs rule for solving large-scale linear systems". Journal of Discrete Algorithms. 10: 98–109. doi:10.1016/j.jda.2011.06.007.

پیوند به بیرون

در ویکی‌کتاب کتابی با عنوان: Linear Algebra/Cramer's Rule وجود دارد.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Cramer, Gabriel (1750). "Introduction à l'Analyse des lignes Courbes algébriques" (به French). Geneva: Europeana. pp. 656–659. Retrieved 2012-05-18.

[2] MacLaurin, Colin (1748). A Treatise of Algebra, in Three Parts.

[3] Boyer, Carl B. (1968). A History of Mathematics (2nd ed.). Wiley. p. 431.

[4] Katz, Victor (2004). A History of Mathematics (Brief ed.). Pearson Education. pp. 378–379.

[5] Hedman, Bruce A. (1999), "An Earlier Date for "Cramer's Rule"", Historia Mathematica, 4(26): 365–368, doi:10.1006/hmat.1999.2247

[6] Ken Habgood, Itamar Arel (2012). "A condensation-based application of Cramerʼs rule for solving large-scale linear systems". Journal of Discrete Algorithms. 10: 98–109. doi:10.1016/j.jda.2011.06.007.

جبر خطی
مفاهیم عمومی	اسکالر (ریاضی) بردار اقلیدسی فضای برداری Scalar multiplication تصویر (بردار) Linear span نگاشت خطی Linear projection استقلال خطی ترکیب خطی پایه (جبر خطی) Column space Row space تعامد (جبر خطی) Kernel ویژه‌مقدار و ویژه‌بردار Outer product فضای ضرب داخلی ضرب داخلی ترانهاده الگوریتم گرام اشمیت دستگاه معادلات خطی
جبر برداری	ضرب خارجی Triple product Seven-dimensional cross product
جبر چندخطی	Geometric algebra Exterior algebra Bivector Multivector
ماتریس	Block Decomposition ماتریس وارون کهاد ضرب ماتریس رتبه (جبر خطی) Transformation قاعده کرامر حذف گاوسی
ساختارهای جبر مجرد	Dual Direct sum Function space Quotient Subspace Tensor product
جبر خطی عددی	ممیز شناور متلب Numerical stability Basic Linear Algebra Subprograms (BLAS) ماتریس خلوت Comparison of linear algebra libraries Comparison of numerical analysis software
رده:جبر خطی Outline Portal Wikibook Wikiversity