همنهشتی (نظریه اعداد)
نظریه همنهشتی یا حساب پیمانهای سیستمی برای محاسبه با اعداد صحیح است که بهوسیله کارل فردریش گاوس در کتاب رساله حساب در سال ۱۸۰۱ معرفی شد.
مفهوم همنهشتی را میتوان به عنوان پالایشی برای نظریه بخش پذیری دانست و بهوسیله آن میتوان مفاهیم بنیادی را در نظریه اعداد مورد مطالعه قرار داد که بدون استفاده از آن بیان و اثبات بسیاری از مطالب در نظریه اعداد دشوار یا غیرممکن خواهد بود. بعلاوه همنهشتیها میتوانند خیلی شبیه به معادلات مورد بحث قرار بگیرند و از این رو رابطهای شبیه به تساوی ایجاد خواهند کرد.
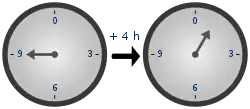
به همین دلیل گاوس نماد را برای همنهشتی معرفی نمود. یکی از کاربردهای مهم همنهشتیها در حل معادلات سیاله است. مفهوم همنهشتی در موارد بسیاری در زندگی ما مشهود است. یکی از کاربردهای آشنا همنهشتیها در زندگی روزمره استفاده از ۲۴ ساعت در شبانه روز است. بهطور کلی هر پدیدهای که به صورت دورهای رخ میدهد بیانگر کاربردی از همنهشتی است.
تعریف
- قرار داد: از این پس حروف m و n بیانگر اعداد طبیعی و حروف ... ,a,b,c بیانگر اعداد صحیح خواهند بود مگر آنکه خلاف آن صریحاً تصریح شود.
گوییم عدد a به پیمانه (سنج) m با b همنهشت است و مینویسیم
- هرگاه
- به بیان دیگر : که
از آنجا که با توجه به این تعریف هر دو عدد طبیعی به پیمانه m=۱ با هم همنهشت میباشند، پیمانه را معمولاً عدد طبیعی بزرگتر از یک در نظر میگیریم. بعلاوه برای سهولت در نوشتار گاهی نماد را برای نمایش همنهشتی به پیمانه m استفاده میکنیم.
اگر a و b به پیمانه m همنهشت نباشد مینویسیم
به عنوان مثال چرا که ولی . وقتی می گوئیم m,aرا عاد می کند یعنیm=ak
همنهشتی به عنوان یک رابطه
همنهشتی به پیمانه دلخواه m یک رابطه را روی مجموعه اعداد صحیح تعریف میکند. این رابطه را به صورت نشان میدهیم و برای هر دو عدد صحیح a,b به صورت:
تعریف میکنیم.
با کمی دقت متوجه میشویم این رابطه یک رابطه همارزی روی مجموعه اعداد صحیح است.
- قضیه۱
- رابطه همنهشتی به پیمانه m روی مجموعه اعداد صحیح یک رابطه همارزی است.
- برهان ۱
- برای هر عدد صحیح a داریم m|a-a پس ولذا رابطه منعکس است.
- برای هر دو عدد صحیح a,b اگر آنگاه بنابه تعریف m|a-b پس m|b-a و در نتیجه و لذا رابطه متقارن است.
- برای هر سه عدد صحیح a,b,c اگر و آنگاه m|a-b و m|b-c حال با توجه به خواص رابطه عاد کردن میتوان نوشت m|a-c پس و لذا رابطه متعدی است.
از ۱و۲و۳ نتیجه میشود رابطه یک رابطه همارزی روی اعداد صحیح تعریف میکند و برهان تمام است.
حال که رابطه یک رابطه همارزی روی اعداد صحیح تعریف میکند، طبیعی است که به دنبال کلاسهای همارزی آن باشیم. در این راه به خاصیت جالبی از رابطه پی خواهیم برد.
اگر برای هر عدد صحیح a کلاس همارزی a به پیمانه m را با نماد نشان دهیم، داریم:
پس
ولذا
در نتیجه
برطبق قوانین حاکم بر کلاسهای همارزی برای هر دو عدد صحیح a,b داریم اگر و فقط اگر
همانند همه روابط همارزی، رابطه همارزی مجموعه اعداد صحیح را به کلاسهای همارزی خود افراز میکند.
با کمی دقت در کلاسهای همارزی این رابطه به سادگی میتوان نشان داد که رابطه مجموعه اعداد صحیح را به دقیقاً m کلاس همارزی افراز میکند. مجموعه خارج قسمت (مجموعه همه کلاسها همارزی) رابطه همارزی به پیمانه را با نشان میدهیم و آن را مجموعه اعداد صحیح به پیمانه m مینامیم.
این مجموعه را بنابر مطلب قبل میتوان به صورت نشان داد.
وضوحاً هر عدد صحیح با یکی از اعضای به پیمانه m همنهشت است.
حلقه اعداد صحیح به پیمانه
دیدیم که رابطه همنهشتی به پیمانه m مجموعه اعداد صحیح را به m کلاس همارزی افراز میکند و مجموعه خارج قسمت آن مجموعه اعداد صحیح به پیمانه m است که به صورت زیر تعریف میشود:
اعمال ⊕,⊗ روی برای هر به صورت زیر تعریف میشود.
به سادگی میتوان تحقیق نمود که به همراه این اعمال تشکیل یک حلقه جابجایی یکدار را میدهد. این بحث در همنهشتیهای جبری بسیار اهمیت دارد.
خواص همنهشتیها
- قضیه۲
- طرفین دو رابطه همنهشتی به یک پیمانه را میتوان باهم جمع یا در هم ضرب کرد. به عبارت دیگر اگر و آنگاه:
- برهان۲
به عنوان نمونه مورد ۱ را اثبات میکنیم. چون بنابه فرض پس m|a-b و چون
پس m|c-d بنابر خوص رابطه عاد کردن داریم (m|(a-b)+(c-d پس (m|(a+c)-(b+d ولذا
مورد ۲ نیز به طریق مشابه اثبات میشود.
قضیه فوق را میتوان به بیش از دو رابطه همنهشتی نیز تعمیم داد. به عبارت دیگر به سادگی به استقراء ثابت میشود اگر برای هر i=1,2,3,.. ,n آنگاه:
- قضیه ۳
- طرفین یک رابطه همنهشتی را میتوان در عددی ثابت ضرب کرد. به عبارت دیگر اگر و c عددی صحیح ثابتی باشد باشد داریم .
- برهان۳
- چون بنابه فرض پس m|a-b ولذا (m|c(a-b در نتیجه m|ac-bc ولذا
دو قضیه اخیر به خوبی شباهت میان رابطه همنهشتی را با رابطه تساوی را نشان میدهد. اما این دو رابطه در برخی موارد دارای تفاوت میباشد.
به عنوان مثال میدانیم که دو طرف یک رابطه تساوی را میتوان بر عددی صحیح ناصفر تقسیم نمود. اما آیا این خاصیت در مورد رابطه همنهشتی به پیمانه دلخواه m صادق است؟
قضیه زیر بیان میکند در تقسیم طرفین یک رابطه همنهشتی بر یک عامل مشترک طرفین پیمانه دچار تغییر میشود.
- قضیه ۴
- فرض کنید c عددی صحیح ناصفر باشد و (d=(c,m در این صورت اگر
آنگاه
- برهان۴
- چون پس m|a-b بنابراین
اما چون (d=(c,m پس و در نتیجه بنابر لم اقلیدس پس
پس اگر c عددی صحیح ناصفر باشد که ، اگر آنگاه
همانطور که اشاره شد رابطه نزدیکی میان رابطه همنهشتی و نظریه بخش پذیری وجود دارد. در حقیقت نظریه همنهشتی را میتوان به عنوان پالایشی برای نظریه بخش پذیری دانست. قضایای زیر به خوبی این رابطه را نشان میدهد.
- قضیه۵
- اگر r باقیمانده تقسیم عدد a بر m باشد آنگاه
- برهان۵
- بنابر قضیه تقسیم عدد صحیح q وجود دارد که a=mq+r پس a-r=mq و لذا m|a-r پس .
- قضیه6
- اگر و فقط اگر باقیمانده تقسیم a و b بر m برابر باشد.
- برهان۶
- ابتدا فرض میکنیم و نشان میدهیم باقیمانده تقسیم a و b بر m برابر است.
چون پس m|a-b ولذا به ازای عدد صحیح q داریم(1) a=b+mq. باقیمانده تقسیم b بر m را r مینامیم. بنابر قضیه تقسیم عدد صحیح k موجود است که (2) b=mk+r.
از (۱) و (۲) داریم
پس باقیمانده تقسیم a برm برابر r است.
حال فرض میکنیم باقیمانده تقسیم a و b بر m برابر r باشد. در این صورت بنابر قضیه تقسیم اعداد صحیح k و q وجود داردند که a=mq+r و b=mk+r پس (a-b=m(q-k ولذا m|a-b پس
دستگاه کامل ماندهها به پیمانه
دستگاههای کامل ماندهها در نظریه همنهشتی به ویژه در حل معادلات همنهشتی نقش اساسی دارند. به عبارت دقیقتر در نهایت برای حل یک معادله همنهشتی کافی است جوابها را در میان اعضای یک دستگاه کامل ماندهها به پیمانه همنهشتی مورد نظر جستجو کنیم.
در تعریف زیر سه شرط را برای دستگاه کامل ماندهها به پیمانه دلخواه m بیان میکنیم ولی به سادگی میتوان تحقیق کرد هر یک از دو شرط زیر دیگری را نتیجه میدهد؛ لذا در متون مختلف ممکن است هر یک از این دو شرط را به عنوان تعریف ذکر کنند.
- تعریف
- مجموعه A از اعداد صحیح را یک دستگاه کامل ماندهها (د. ک. م یا دسکم) به پیمانه m میگوییم هرگاه واجد شرایط زیر باشد:
- A دارای m عضو متمایز چون a1,a2,a3,... ,am باشد.
- اعضای A دو به دو به پیمانه m ناهمنهشت باشند.
- هر عدد صحیح با یک و فقط یک عضو A به پیمانه m همنهشت باشد.
سادهترین دستگاه کامل ماندهها به پیمانه m مجموعه {A={0,1,2,3,... ,m-۱ است. در حقیقت قضیه زیر را داریم:
- قضیه۷
- مجموعه {A={0,1,2,3,... ,m-۱ یک دستگاه کامل ماندهها به پیمانه m است.
دستگاه مخفف ماندهها به پیمانه
مجموعه A از اعداد صحیح را یک دستگاه مخفف ماندهها (د. م. م یا دمم) به پیمانه m میگوییم هرگاه واجد شرایط زیر باشد:
- A دارای عضو متمایز باشد؛ که در آن همان تابع فی اویلر است.
- اعضای A نسبت به m اول باشند و دو به دو به پیمانه m ناهمنهشت باشند.
- هر عدد صحیح که نسبت به پیمانه m اول است با یک و فقط یکی از اعضای A به پیمانه m همنهشت باشد.
جستارهای وابسته
- معادلات همنهشتی
- همنهشتیهای جبری
- قضیه اویلر
- قضیه کوچک فرما
- مرتبه
- قضیه ویلسون
- قضیه باقیمانده چینی
منابع
- ویلیام دبلیو. آدامز، لری جوئل گولدشتین (۱۳۸۴)، آشنایی با نظریه اعداد، ترجمهٔ دکتر آدینه محمد نارنجانی، تهران: مرکز نشر دانشگاهی، شابک ۹۶۴-۰۱-۰۰۷۰-۶
- تام آپوستل (۱۳۷۶)، نظریه تحلیلی اعداد (۱)، ترجمهٔ دکتر علیاکبر عالمزاده-علیاکبر رحیمزاده، تهران: نشر منصوری، شابک ۹۶۴-۶۱۶۶-۰۶-۷
- مشارکتکنندگان ویکیپدیا. «Modular arithmetic». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲۴ اوت ۲۰۰۷.