رابطه بازتابی
در ریاضیات، رابطهٔ بازتابی[1] (به انگلیسی: Reflexive relation) رابطهای است که برای یک مجموعهٔ ناتُهی تعریف میشود و به رابطهٔ دوتاییای میگویند که همهٔ عناصر مجموعه آن رابطه را با خودشان داشته باشند.[2]
|
هر رابطهٔ همانی یک رابطهٔ بازتابی است با این حال هر رابطهٔ بازتابی لزوماً همانی نیست.[3]
مثال «1»
اگر و رابطهٔ دوتایی به صورت تعریف شود، آنگاه یک رابطهٔ بازتابی خواهد بود. ولی رابطهٔ بازتابی نیست زیرا با وجود اینکه ، اما .[4]
ماتریس متناظر با رابطه بازتابی
ماتریس متناظر با رابطه ی بازتابی، ماتریسی است که همه ی درایه های قطر اصلی آن یک باشد. بنابرین ماتریس M = [mi,j] با n سطر و n ستون دارای خاصیت بازتابی است اگر:
مثال «2»
ماتریس دارای خاصیت بازتابی است زیرا تمام درایه های قطر اصلی آن یک هستند.ولی ماتریس دارای خاصیت بازتابی نیست زیرا تمام درایه های قطر اصلی آن یک نیستند.
گراف متناظر با رابطه بازتابی
گراف متناظر با رابطه ی بازتابی، گرافی است که تمام رئوس آن دارای حلقه (loop) باشد.
مثال «3»
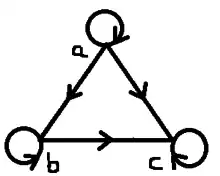
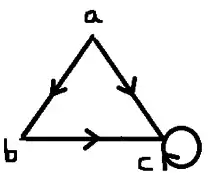
تصویر 1 نشان دهنده ی گرافی است که دارای خاصیت بازتابی است زیرا تمام رئوس آن دارای حلقه است .و تصویر 2 نشان دهنده ی گرافی است که خاصیت بازتابی ندارد زیرا رئوس a,b آن دارای حلقه نمی باشند.
بستار بازتابی رابطه R
اگر رابطه دارای خاصیت بازتابی نباشد رابطه ی که شامل بوده و خاصیت بازتابی نیز دارد و زیر مجموعه ی هر رابطه ی دیگری که شامل است نیز باشد بستار بازتابی رابطه ی نامیده می شود.
مثال «4»
همانطور که در مثال 1 دیدید رابطهٔ بازتابی نیست.حال اگر زوج مرتب را به رابطه ی بیفزاییم رابطه ی بدست می آید که همان بستار بازتابی رابطه ی نامیده می شود.
جستارهای وابسته
پانویس
- «رابطهٔ بازتابی» [ریاضی] همارزِ «reflexive relation»؛ منبع: گروه واژهگزینی. جواد میرشکاری، ویراستار. دفتر پنجم. فرهنگ واژههای مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۷۸-۹۶۴-۷۵۳۱-۷۶-۴ (ذیل سرواژهٔ رابطهٔ بازتابی)
- «رابطهٔ بازتابی» [ریاضی] همارزِ «reflexive relation»؛ منبع: گروه واژهگزینی. جواد میرشکاری، ویراستار. دفتر پنجم. فرهنگ واژههای مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۷۸-۹۶۴-۷۵۳۱-۷۶-۴ (ذیل سرواژهٔ رابطهٔ بازتابی)
- Chakrabarti, p. 1-PA402.
- Saleem, p. 5.
منابع
- Saleem, S.K. AIEEE Mathematics. Sura Books. ISBN 978-81-7254-292-4. Retrieved March 7, 2016.
- Chakrabarti, J. ISC Mathematics. Allied Publishers. ISBN 978-81-8424-303-1. Retrieved March 7, 2016.
- Rosen, Kenneth H. Discrete Mathematics and Applications. Raghothaman Srinivasan. ISBN 978-0-07-338309-5.
