قطعه دایره
در هندسه، قطعه دایره بخشی از سطح دایره است که میان محل برش وتری از دایره و کمانی از آن قرار دارد. این بریدگی میتواند ناشی از یک خط یا یک پارهخط (وتر دایره) باشد. قطعهٔ دایره نباید مرکز دایره را در خود داشته باشد.
رابطهها
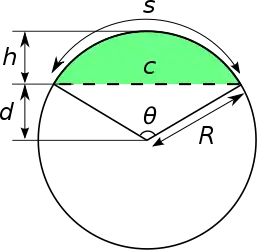
در نظر بگیرید R شعاع دایره و θ یک زاویهٔ مرکزی است بر حسب رادیان. اگر طول وتر دایره را c، طول کمان را s و ارتفاع قطعه را h بنامیم و d ارتفاع سه گوش (مثلث) پایینی باشد، آنگاه میتوان گفتههای زیر را نتیجه گرفت:
- شعاع دایره برابر است با
- طول کمان برابر است با
- طول وتر برابر است با
- ارتفاع برابر است با
- زاویه برابر است با
مساحت
مساحت قطعهٔ دایره برابر است با سطح ناحیهٔ محدود به کمان دایره بدون مساحت مثلث پایینی:
بدست آوردن شعاع به کمک خطکش
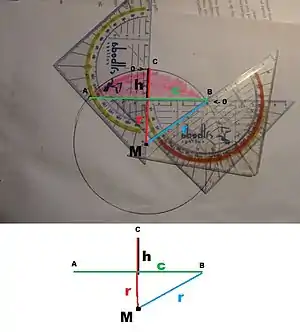
راه دیگری که به کمک آن بتوان شعاع دایره را بدست آورد استفاده از چند خطکش است به این ترتیب که اول یک خطکش را بر روی وتر قرار میدهیم آنگاه که وسط وتر را یافتیم خطکش دیگر را عمود بر آن قرار میدهیم و نقطهٔ C را علامت میزنیم، آنگاه خطکش دیگری را بر روی نقطهٔ B قرار میدهیم و آن قدر آن را جابجا میکنیم تا طول محل برخورد دو خطکش با هم برابر شود آن نقطه را M مینامیم، پاره خط MC و MB هر دو شعاعهای دایرهٔ مربوط به قطعهٔ دایرهاند. زاویهٔ BMC نیز برابر با ½ است.
به روش گفته شده، روش شعاع پیترو-ولما (به انگلیسی: Pietrow-Vollema) نیز میگویند.
جستارهای وابسته
پیوند به بیرون
- Weisstein, Eric W. "Circular segment". MathWorld.
- تعریف قطعهٔ دایره همراه با پویانمایی
- رابطههای مربوط به مساحت قطعهٔ دایره همراه با پویانمایی

