شبکه جهانکوچک
یک شبکه جهانکوچک نوعی گراف است که در آن گرههای زیادی با هم همسایه نیستند اما همسایگان هر کدام از گرهها با احتمال زیادی به هم متصل هستند و در نتیجه با تعداد گام کمی میتوان از هر گره به گره دیگر رسید. شبکهای را شبکه جهانکوچک میگوییم که فاصله معمول بین دو راس تصادفی از آن (L) ضریبی از لگاریتم تعداد کل گرهها در شبکه (N) باشد.[1]
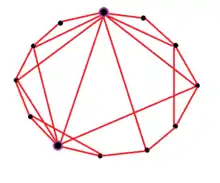
میانگین طول کوتاهترین مسیر بین دو راس = 1.803.
ضریب خوشگی = ۰٫۵۲۲
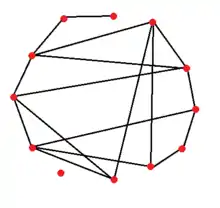
این در حالی است که ضریب خوشگی در این شبکهها کوچک نیست به این معنی که گرهها تمایل به ایجاد خوشه دارند. در علم شبکههای اجتماعی این ویژگیها نشان دهنده پدیده جهانکوچک هستند که در آن غریبهها با زنجیره کوتاهی از آشنایان به یکدیگر متصل میشوند. بسیاری از گرافهای تجربی اثر جهانکوچک را در خود نشان دادهاند، برای مثال، شبکههای اجتماعی، اینترنت، ویکیپدیا و شبکههای ژنی.
نوع خاصی از شبکههای جهانکوچک گرافهای تصادفی هستند. که در سال ۱۹۹۸ توسط دانکن وات و استیون استروگاتز شناسایی شدند.[2] آنها در مقاله خود عنوان کردند که گرافها را میتوان بر اساس دو ویژگی ساختاری طبقهبندی کرد، ضریب خوشگی و متوسط فاصله گره تا گره(میانگین طول کوتاهترین مسیر). در گرافهای کاملاً تصادفی مثل مدل اردوش-رنیی میانگین طول کوتاهترین مسیر کم است (این طول متغیر و معمولاً به اندازه لگاریتم تعداد گرهها است) و همچنین ضریب خوشگی کوچکی دارند. واتز و استروگاتز با اندازهگیریهای خود نشان دادند که بسیاری از شبکههای دنیای واقعی میانگین طول کوتاهترین مسیر کم و همچنین ضریب خوشگی بیشتری از مقدار مورد انتظار در یک گراف تصادفی دارند. یعنی در گرافهای دنیای واقعی تمایل بیشتر برای خوشه شدن نسیت به گراف تصادفی وجود دارد. با در نظر گرفتن این موارد واتز و استروگاتز مدل جدیدی را پیشنهاد دادند که (۱) میانگین طول کوتاهترین مسیر کم و(۲) ضریب خوشگی زیادی داشت.
ویژگیهای شبکههای جهانکوچک
شبکههای جهانکوچک تمایل دارند گروهک (زیرگراف کامل) و شبهگروهک داشته باشند، زیر گرافهایی که بیشتر گرهها در آن دوبهدو به هم وصلاند. این ویژگی از تعریف ضریب خوشگی بالا هم به دست میآید. دومین ویژگی گراف این شبکه این است که بیشتر جفت گرهها با حداقل یک مسیر کوتاه به هم متصل شدهاند. این ویژگی هم از کم بودن میانگین طول کوتاهترین مسیر بین دو گره به دست میآید. شبکههای جهانکوچک چند ویژگی دیگر را هم همراه با خود دارند. بهطور معمول تعداد زیادی قطب (گرههایی با درجه و اتصالهای زیاد) در شبکه وجود دارد. این قطبها اتصالهای مشترک برای شکلگیری کوتاهترین مسیرها را تأمین میکنند. در مقیاس کوچک، در شبکه جهانکوچک پروازهای هواپیمایی میانگین طول مسیر کم است زیرا بسیاری از مسیرهای پرواز از شهرهایی که (قطب) هستند میگذرد. این ویژگی معمولاً با نسبت گرهها با تعداد اتصالهای مشخص سنجیده میشود (توزیع درجه شبکه). شبکههایی که تعداد گره قطب زیاد، گرههای بیشتری با درجه زیاد خواهند داشت و در نتیجه توزیع درجههای آنها در درجههای زیاد بالا خواهد بود که به آن شبکه با توزیع دمکلفت میگویند.
جهانکوچک بودن شبکه با یک ضریب، سنجیده میشود. این ضریب با مقایسه خوشگی و طول مسیر شبکه داده شده با یک گراف تصادفی معادل با میانگین درجه یکسان به دست میآید.[3][4]
که در آن مشخصه طول مسیر L و ضریب خوشگی C از شبکه مورد آزمایش محاسبه میشوندو Cr ضریب خوشگی و Lr مشخصه طول مسیر برای شبکه تصادفی معادل است.
در صورتی که شبکه، جهانکوچک است.
دو دانشمند به نامهای کوهن(R. Cohen) وهاولین(Shlomo Havlin) نشان دادند[5][6] که شبکههای مستقل از مقیاس ابر-جهانکوچک هستند. در این شبکهها به دلیل وجود قطبها کوتاهترین مسیر بهطور قابل توجهی کوچک میشود و مقیاس آنها برابر میشود با:
نمونههایی از شبکههای جهانکوچک
ویژگیهای جهانکوچک در بسیاری از پدیدههای دنیای واقعی یافت میشود؛ مثلاً زنجیرهٔ غذایی، شبکه توزیع برق، شبکه سلولهای عصبی مغز، شبکه رایدهندگان، شبکه تماسهای تلفنی، شبکه نفوذ اجتماعی، شبکههای فرهنگی[8] و شبکههای روابط[9] .
شبکه تعامل پروتئین-پروتئین خواص جهانکوچک را دارد.[10] همچنین شبکههای رونویسی که در آن گرهها ژنها هستند و در صورتی به هم متصلاند که یک ژن تأثیر ژنتیکی بالا یا پایین بر روی دیگری داشته باشد، هم ویژگیهای جهانکوچک دارد.[11]
ساخت شبکههای جهانکوچک
مهمترین سازوکار ساخت شبکه جهانکوچک، استفاده از مدل واتز و استروگاتز است.
جستارهای وابسته
منابع
- http://www.nature.com/nature/journal/v393/n6684/full/393440a0.html
- Watts, Duncan J.; Strogatz, Steven H. (June 1998). "Collective dynamics of 'small-world' networks". Nature. 393 (6684): 440–442. Bibcode:1998Natur.393..440W. doi:10.1038/30918. PMID 9623998.CS1 maint: Multiple names: authors list (link) Papercore Summary http://www.papercore.org/Watts1998
- The brainstem reticular formation is a small-world, not scale-free, network M. D. Humphries, K. Gurney and T. J. Prescott, Proc. Roy. Soc. B 2006 273, 503–511, doi:10.1098/rspb.2005.3354
- Humphries and Gurney (2008). "Network 'Small-World-Ness': A Quantitative Method for Determining Canonical Network Equivalence". PLOS ONE. 3 (4): e0002051. doi:10.1371/journal.pone.0002051. PMC 2323569. PMID 18446219.
- R. Cohen, S. Havlin, and D. ben-Avraham (2002). "Structural properties of scale free networks". Handbook of graphs and networks. Wiley-VCH, 2002 (Chap. 4).
- R. Cohen, S. Havlin (2003). "Scale-free networks are ultrasmall". Phys. Rev. Lett. 90 (5): 058701. arXiv:cond-mat/0205476. Bibcode:2003PhRvL..90e8701C. doi:10.1103/PhysRevLett.90.058701. PMID 12633404.
- Esfahani, Reihaneh Kouhi; Shahbazi, Farhad; Samani, Keivan Aghababaei (2012-09-06). "Noise-induced synchronization in small world networks of phase oscillators". Physical Review E. 86 (3): 036204. doi:10.1103/PhysRevE.86.036204.
- "'n Kwantifisering van kleinwêreldsheid in Afrikaanse kultuurnetwerke in vergelyking met ander komplekse netwerke | LitNet". LitNet. 2015-11-05. Retrieved 2017-02-27.
- "Die statistiese eienskappe van geskrewe Afrikaans as 'n komplekse netwerk | LitNet". LitNet. 2017-02-09. Retrieved 2017-02-27.
- Bork, P.; Jensen, LJ; von Mering, C.; Ramani, A.; Lee, I.; Marcotte, EM. (2004). "Protein interaction networks from yeast to human" (PDF). Current Opinion in Structural Biology. 14 (3): 292–299. doi:10.1016/j.sbi.2004.05.003. PMID 15193308.
- Van Noort, V; Snel, B; Huynen, MA. (Mar 2004). "The yeast coexpression network has a small-world, scale-free architecture and can be explained by a simple model". EMBO Rep. 5 (3): 280–4. doi:10.1038/sj.embor.7400090. PMC 1299002. PMID 14968131.
