بیشینه هموار

در ریاضیات تابع بیشینهٔ هموار (به انگلیسی: softmax function) یا تابع نمایی نرمال‌سازی‌شده (به انگلیسی: normalized exponential function)[1]^:198 تعمیم تابع لجستیک است. تابع بیشینهٔ هموار یک بردار $K$ -تایی از اعداد حقیقی مانند $Z$ را به عنوان ورودی دریافت می‌کند و بردار $K$ -تایی $\sigma (Z)$ از مقادیر حقیقی $[0,1]$ را به عنوان خروجی می‌دهد که جمع مولفه‌های آن ۱ می‌شود. ضابطه تابع به شرح زیر است:

$\sigma (Z)_{j}={\frac {e^{Z_{j}}}{\sum _{k=1}^{K}e^{Z_{k}}}}$ for j = 1, …, K.

خروجی تابع بیشینه‌هموار، در نظریه احتمالات می‌تواند برای نمایش یک توزیع رسته‌ای (به انگلیسی: categorical distribution) استفاده شود. توزیع رسته‌ای، توزیع احتمالاتی بر روی $K$ نتیجه مختلف است.

تابع بیشینه‌هموار در روش‌های طبقه‌بندی متعددی استفاده می‌شود؛ مانند: رگرسیون لجستیک چندجمله‌ای[1]^:206–209 (به انگلیسی: multinomial logistic regression)، آنالیز افتراقی خطی، دسته‌بندی کننده بیز ساده و شبکه عصبی مصنوعی.[2] در رگرسیون لجستیک چندجمله‌ای و آنالیز افتراقی خطی، ورودی تابع، خروجی $K$ تابع خطی است و در صورتی که بردار نمونه ورودی $x$ و بردار وزن‌ها $w$ باشد، احتمال پیش‌بینی شده برای کلاس $j$ ام برابر است با:

$P(y=j\mid \mathbf {x} )={\frac {e^{\mathbf {x} ^{\mathsf {T}}\mathbf {w} _{j}}}{\sum _{k=1}^{K}e^{\mathbf {x} ^{\mathsf {T}}\mathbf {w} _{k}}}}$

که $w_{j}$ سطر $j$ ام بردار وزن‌هاست و $\mathbf {x} ^{\mathsf {T}}\mathbf {w} _{j}$ هم برابر با مقدار ضرب داخلی بردارهای ورودی و بردار وزن است. در توصیف دیگری از عبارت بالا به جای ضرب داخلی، می‌توان از عملیات ترکیب توابع استفاده کرد؛ یعنی عبارت بالا به صورت ترکیب $K$ تابع خطی $\mathbf {x} \mapsto \mathbf {x} ^{\mathsf {T}}\mathbf {w} _{1},\ldots ,\mathbf {x} \mapsto \mathbf {x} ^{\mathsf {T}}\mathbf {w} _{K}$ و تابع بیشینه‌هموار تلقی گردد. به عبارت دیگر عملگری که با استفاده از بردار وزن تعریف شده‌است، بر روی ورودی اعمال شده و ورودی را به برداری در فضای $R^{K}$ انتقال می‌دهد.[3]

مقایسه تابع بیشینه به رنگ آبی و تابع بیشینه هموار به رنگ قرمز. تابع بیشینه هموار تقریب مشتق پذیری از تابع بیشینه ارائه می‌کند.

علت نام‌گذاری

از دو منظر می‌توان علت این نام‌گذاری را بررسی کرد؛ معنی اصلی و معنی در یادگیری ماشین.

معنی اصلی

معنی دیدگاه اول این است که تابع $max(x_{1},x_{2},\ldots ,x_{n})$ تابعی با دامنه و برد $R^{n}\to R$ است؛ ولی این تابع پیوسته نیست و به همین دلیل نمی‌توان مشتق آن را تعریف کرد؛ بنابراین در بسیاری از کاربردها از تابع زیر:

${\text{softmax}}(x_{1},x_{2},\ldots ,x_{n})=log(\sum _{i=1}^{n}e^{x_{i}})$

استفاده می‌شود. تابع بیشینهٔ هموار، تقریب هموار و پیوسته‌ای از تابع بیشینه (به انگلیسی: maximum function) ارائه می‌کند که مشتق‌پذیر است.

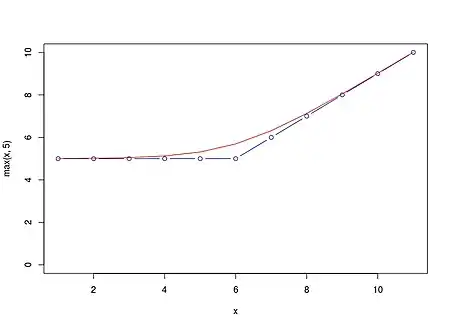
در شکل مقابل دو تابع ${\text{max}}(x,5)$ و ${\text{softmax}}(x,5)$ در بازه $[0,10]$ مقایسه شده‌اند. تابع بیشینه هموار (قرمز رنگ) تقریب مشتق پذیری از تابع بیشینه (آبی رنگ) ارائه می‌کند.

معنی در یادگیری ماشین

در یادگیری ماشین به منظور انجام طبقه‌بندی (به انگلیسی: classification) از تابع بیشینهٔ هموار استفاده می‌شود. به طور مثال در صورتی که $n$ کلاس مختلف وجود داشته باشد و الگوریتم یادگیری ماشین به طور مستقیم احتمال حضور ورودی در هر کدام از این کلاس‌ها را تولید نکند و به جای آن، برداری از $n$ عدد حقیقی که متناظر با امتیاز قرارگیری ورودی در هر دسته است، خروجی دهد، می‌توان از تابع زیر برای تبدیل امتیازهای حقیقی به احتمال استفاده کرد؛ بدین ترتیب شرایط تعریف یک تابع جرم احتمال (قرارگیری در $[0,1]$ و جمع احتمالات برابر با ۱) رعایت خواهد شد:

$(p_{1},\ldots ,p_{n})=f(s_{1},\ldots ,s_{n})=({\frac {e^{s_{1}}}{\sum _{i=1}^{n}e^{s_{i}}}},\ldots ,{\frac {e^{s_{n}}}{\sum _{i=1}^{n}e^{s_{i}}}})$

که در آن $p_{1}$ تا $p_{n}$ مقادیر مطلوب احتمال و $s_{1}$ تا $s_{n}$ مقادیر حقیقی امتیازهای هر کلاس هستند.

حال پس از بررسی ضابطه تابع $f$ می‌توان متوجه شد که این عبارت برابر با ضابطه تابع گرادیان بیشینهٔ هموار است.[4]

$f=\nabla {\text{softmax}}(s_{1},\ldots ,s_{n})$

مثال

اگر ورودی $(5,2,3,1,2,3)$ باشد، مقدار تابع بیشینهٔ هموار برابر با بردارِ $(0.720,0.036,0.097,0.013,0.036,0.097)$ خواهد بود. همان‌طور که در قسمت قبل اشاره شد، به دلیل نمایی بودن تابع بیشینهٔ هموار، مقدار خروجی متناظر با عدد بیشینه در ورودی، از خروجی بقیه اعداد به مراتب بیشتر شده‌است.

در زیر کد این تابع با ورودی مثال، به زبان R آمده‌است:

> softmax <- function(inp) {
+ s <- sum(exp(inp))
+ return(exp(inp)/s)
+ }
>
> inp <- c(5, 2, 3, 1, 2, 3)
> softmax(inp)
[1] 0.72017036 0.03585517 0.09746446 0.01319038 0.03585517 0.09746446

شبکه‌های عصبی مصنوعی

می‌توان از تابع بیشینهٔ هموار در لایه آخر شبکه‌های عصبی مصنوعی استفاده کرد[5]. چنین شبکه‌های عصبی معمولاً به وسیله یک تابع اختلاف آنتروپی (به انگلیسی: Cross Entropy) تعلیم داده می‌شوند و یک حالت غیرخطی از تابع رگرسیون لجستیک چندجمله‌ای حاصل می‌شود.

به دلیل اینکه تابع، یک بردار و یک اندیس مشخص را به یک عدد حقیقی نگاشت می‌کند، این اندیس در مشتقات نیز ظاهر می‌شود:

${\frac {\partial }{\partial q_{k}}}\sigma ({\textbf {q}},i)=\cdots =\sigma ({\textbf {q}},i)(\delta _{ik}-\sigma ({\textbf {q}},k))$

در اینجا از تابع دلتا کرونکر استفاده شده‌است.

یادگیری تقویتی

در حوزه یادگیری تقویتی شبیه آنچه در قسمت نام‌گذاری گفته شد، از تابع بیشینهٔ هموار می‌توان برای تبدیل مقادیر به احتمال کنش استفاده کرد.[6]

ضابطه تابعی که به طور متداول استفاده می‌شود برابر است با:

$P_{t}(a)={\frac {\exp(q_{t}(a)/\tau )}{\sum _{i=1}^{n}\exp(q_{t}(i)/\tau )}}{\text{,}}$

که در این تابع مقدار کنش $q_{t}(a)$ متناظر است با امتیاز پیش‌بینی شدهٔ آن عمل $a$ و از $\tau$ نیز به عنوان پارامتر دما یاد می‌شود (با اشاره به مکانیک آماری). برای دماهای بالا ( $\tau \to \infty$ ) تقریباً همه کنش‌ها احتمال یکسانی دارند و هرچه دما پایین‌تر باشد، مقدار پیش‌بینی شدهٔ تأثیر جایزه بر احتمال بیشتر است. در دمای کم ( $\tau \to 0^{+}$ ) احتمال مربوط به کنشی که بیشترین امتیاز نسبت به سایر کنش‌ها را دارد، به ۱ میل می‌کند.

نرمال‌سازی بیشینهٔ هموار

نرمال‌سازی بیشینهٔ هموار یا نرمال‌سازی سیگموید، روشی برای کاهش اثر داده‌های پرت بدون حذف این داده‌ها از مجموعه است. وجود این داده‌های پرت می‌تواند مفید باشد در صورتی که بتوان مقدار قابل توجهی از داده‌ها را در شعاع یک واحد انحراف معیار از میانگین نگه داشت.

داده‌ها به صورت غیرخطی به وسیله یکی از توابع سیگموید انتقال داده می‌شوند:

تابع سیگموید لجستیک:[7]

$x_{i}'\equiv {\frac {1}{1+e^{-(x_{i}-\mu _{i})/\sigma _{i}}}}$

تابع تابع_هذلولوی، $tanh$ :[7]

x_{i}'\equiv {\frac {1-e^{-(x_{i}-\mu _{i})/\sigma _{i}}}{1+e^{-(x_{i}-\mu _{i})/\sigma _{i}}}}

تابع سیگموید بازه اعداد را به محدوده صفر تا یک نگاشت می‌کند. این تابع در محدوده میانگین تقریباً خطی است و در دو سر طیف مقادیر آن، شیب ملایمی دارد و به این ترتیب از محدود بودن برد آن و کراندار بودن آن اطمینان حاصل می‌شود. همچنین این خاصیت موجب می‌شود بیشتر مقادیر در فاصله یک واحد انحراف معیار نسبت به میانگین قرار گیرند.

تابع تانژانت هذلولوی مقادیر ورودی را به بازی -۱ تا ۱ نگاشت می‌کند. این تابع در نزدیک میانگین تقریباً خطی است ولی شیبی تقریباً برابر با نصف شیب تابع سیگموید دارد. مانند تابع سیگموید، این تابع در همه نقاط برد مشتق پذیر است و جهت شیب آن توسط نرمال‌سازی تأثیری نمی‌بیند. این خاصیت به الگوریتم‌های عددی و الگوریتم‌های بهینه‌سازی اطمینان می‌دهد که تغییر مشتق تابع پس از نرمال‌سازی روند مشابهی با داده‌های اولیه (پیش از نرمال‌سازی) دارد.

ارتباط آن با توزیع بولتسمان

احتمال یافتن یک اتم در سطح انرژی کوانتومی $\varepsilon _{i}$ هنگامی که این اتم جزئی از یک گروه باشد که آن گروه به تعادل دمایی در دمای $T$ رسیده‌است، برابر با مقدار تابع بیشینهٔ هموار است که از آن به عنوان توزیع بولتسمان یاد می‌شود. مقدار متوسط اشتغال شدن هر سطح برابر با $e^{-\varepsilon _{i}/k_{B}T}$ است و این مقدار نرمال‌سازی شده تا جمع انرژی ۱ شود. در چنین محیطی، ورودی تابع بیشینهٔ هموار مقدارِ منفیِ انرژی هر سطح کوانتومی تقسیم بر $k_{B}T$ است.

منابع

Bishop, Christopher M. (2006). Pattern Recognition and Machine Learning. Springer.
ai-faq What is a softmax activation function?
Wikipedia contributors. "Multinomial Logistic Regression". Retrieved 20 August 2017.
Charles Yang Zheng. "What does the term soft max mean in the context of machine learning". Retrieved 23 August 2017.
Michael A. Nielsen (2015). Neural Networks and Deep Learning. Determination Press. line feed character in |title= at position 20 (help)
Sutton, R. S. and Barto A. G. Reinforcement Learning: An Introduction. The MIT Press, Cambridge, MA, 1998.Softmax Action Selection بایگانی‌شده در ۲۵ ژوئن ۲۰۱۶ توسط Wayback Machine
Artificial Neural Networks: An Introduction. 2005. pp. 16–17.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[bishop-1] Bishop, Christopher M. (2006). Pattern Recognition and Machine Learning. Springer.

[2] -faq What is a softmax activation function?

[3] Wikipedia contributors. "Multinomial Logistic Regression". Retrieved 20 August 2017.

[4] Charles Yang Zheng. "What does the term soft max mean in the context of machine learning". Retrieved 23 August 2017.

[5] Michael A. Nielsen (2015). Neural Networks and Deep Learning. Determination Press. line feed character in |title= at position 20 (help)

[6] Sutton, R. S. and Barto A. G. Reinforcement Learning: An Introduction. The MIT Press, Cambridge, MA, 1998.Softmax Action Selection بایگانی‌شده در ۲۵ ژوئن ۲۰۱۶ توسط Wayback Machine

[ReferenceA-7] Artificial Neural Networks: An Introduction. 2005. pp. 16–17.