گراف جهتدار
در ریاضیات و بهطور خاص در نظریهٔ گراف، گراف جهتدار یا گراف سودار[1] گرافی (مجموعهای از گرهها که با یالها به هم متصل شدهاند) است که در آن به هر یال جهتی نسبت داده شدهاست. به زبان ریاضی، یک گراف جهتدار زوج مرتبی به صورت است (گاهی به صورت نیز نمایش داده میشود) که در آن[2]
- V مجموعهایست که اعضایش را رأس یا گره مینامند
- A مجموعهای از زوجهای مرتبی از رأسها است که کمان، یال جهتدار، فلش یا گاهی یال نامیده میشوند (که در حالت اخیر مجموعهٔ متناظر را به جای A، با E نمایش میدهند).
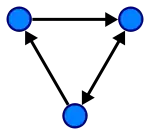
گراف جهت دار با گراف معمولی عمده تفاوتشان در تعاریف یال هاست. یعنی زوج مرتب (a,b) با زوج مرتب (b ,a) تفاوتی در گراف معمولی یا بدون جهت ندارد و در حالت کلی تر آن را به شکل ab می نویسیم ولی در گراف جهت دار زوج مرتب های (a,b) با (b,a) تفاوت دارد و نشان دهنده سوی یال است و نشان دهنده ی نحوه ی ارتباط بین این دو راس می باشد.
یک گراف جهتدار ساده نامیده میشود اگر هیچ طوقه و یال چندگانهای نداشته باشد (یالهای چندگانه یعنی یالهایی که ابتدا و انتهای یکسانی دارند). در یک گراف چندگانهٔ جهتدار یالها تشکیل یک مجموعهٔ چندگانه (به جای مجموعه) از زوجهای مرتب رأسها میدهند و این گرافها میتوانند طوقه و یال چندگانه داشته باشند (طوقه یالی است که ابتدا و انتهایش رأس یکسانی است). در برخی متون، گراف جهتدار (بدون ذکر ویژگی ساده بودن) میتواند طوقه، یال چندگانه یا هر دو را داشته باشد.
اصطلاحات پایهای
یال دارای جهت از به در نظر گرفته میشود. ابتدا و انتهای یال نامیده میشود. را رأس مابعد مستقیم و را رأس ماقبل مستقیم مینامند. اگر مسیری متشکل از یک یا چند یال رو به جلو از به وجود داشته باشد، به رأس مابعد و به رأس ماقبل میگویند. به یال معکوس یال میگویند.
جهتدار کردن یک گراف سادهٔ بدون جهت یعنی نسبت دادن جهت به هر یال آن گراف. هر گراف جهتداری که به این طریق ساخته شود گراف جهتدار شده (به انگلیسی: oriented graph) نامیده میشود. یک گراف جهتدار، یک گراف سادهٔ جهتدار شدهاست اگر و تنها اگر نه طوقه داشته باشد و نه حلقهٔ دوتایی (یال چندگانه). [3]
گراف جهتدار وزندار (به انگلیسی: weighted digraph) گراف جهتداری است که به هر یالش وزنی نسبت داده شدهاست، درست مانند گراف بدون جهت وزندار. در نظریهٔ گراف به گراف جهتدار با یالهای وزندار، شبکه (به انگلیسی: network) میگویند.
ماتریس مجاورت (به انگلیسی: adjacency matrix) یک گراف جهتدار (با طوقه و یالهای چندگانه) ماتریسی دارای مقادیر صحیح است که سطرها و ستونهایش متناظر با گرهها هستند و در آن، مؤلفهٔ غیر قطری تعداد یالها از رأس i به رأس j و مؤلفهٔ قطری تعداد طوقههای رأس i است. ماتریس مجاورت یک گراف جهتدار (با یکسان در نظر گرفتن جایگشتهای سطرها و ستونها) یکتاست. نمایش ماتریسی دیگری برای یک گراف، ماتریس وقوع(به انگلیسی: incidence matrix) آن است.
درجهٔ ورودی و درجهٔ خروجی
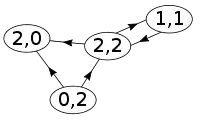
برای هر گره، تعداد رأسهای ابتدایی مجاور، درجهٔ ورودی (به انگلیسی: indegree) و تعداد رأسهای انتهایی مجاور، درجهٔ خروجی (به انگلیسی: outdegree) (در درختها ضریب انشعاب(به انگلیسی: branching factor)) نامیده میشود.
درجهٔ ورودی با و درجهٔ خروجی با نمایش داده میشود. رأس با صفر منبع (به انگلیسی: source) نامیده میشود (چون مبدأ همهٔ یالهای متصل به خودش است) و بهطور مشابه رأس با صفر چاه (به انگلیسی: sink) نامیده میشود.
رابطهٔ مجموع درجات بیان میکند که برای یک گراف جهتدار:
اگر برای هر گرهٔ v ∈ V، گراف را یک گراف جهتدار متعادل (به انگلیسی: balanced digraph) مینامیم. [4]
همبندی گراف جهتدار
میگوییم یک گراف جهتدار ضعیفاً همبند است (به انگلیسی: weakly connected) (یا همبند است [5]) اگر گراف زمینهٔ آن (که با حذف جهت یالها به دست میآید) یک گراف همبند باشد. میگوییم یک گراف جهتدار قویاً همبند است (به انگلیسی: strongly connected) (یا قوی است) اگر برای هر جفت رأس u و v مسیر جهتداری از u به v و مسیر جهتداری از v به u داشته باشد. مؤلفههای قوی (به انگلیسی: strong components)، زیرگرافهای قویاً همبند ماکزیمال هستند.
انواع گرافهای جهتدار
گراف جهتدار G متقارن (به انگلیسی: symmetric) نامیده میشود اگر برای هر کمان متعلق به G، معکوس آن کمان نیز متعلق به G باشد. یک گراف جهتدار متقارن بدون طوقه معادل یک گراف بدون جهت است که با گذاشتن یک یال به جای هر جفت کمان معکوس هم به دست میآید (و بنابراین تعداد یالهایش نصف تعداد کمانهای گراف اولیه است).

یک گراف جهتدار بیدور (به انگلیسی: acyclic) یا گراف بیدور جهتدار، گرافی جهتدار است که هیچ دور جهتداری ندارد. درختهای چندگانه (به انگلیسی: multitrees) (گرافهایی که در آنها هیچ دو مسیر جهتداری که از یک گره شروع شدهاند دوباره در یک گرهٔ مشترک تمام نمیشوند)، درختهای جهتدار (به انگلیسی: oriented trees) یا چنددرختها (به انگلیسی: polytrees) (گرافهای جهتداری که از جهتدار کردن یالهای یک گراف بدون جهت بیدور ساخته میشوند) و درختهای ریشهدار (به انگلیسی: rooted trees) (درختهای جهتداری که تمام یالهای درخت بدون جهت زمینهٔ آن به سمت دور شدن از ریشه جهتدار شدهاند) حالتهایی خاص از گرافهای جهتدار بیدور هستند.

یک تورنمنت (به انگلیسی: tournament) گرافی جهتدار است که از جهتدار کردن همهٔ یالهای یک گراف کامل (به انگلیسی: complete graph) بدون جهت به دست میآید.
در نظریهٔ گروههای لی، یک quiver، گرافی جهتدار است که دامنهٔ نمایش v (که به عنوان عملگر تعریف شده) میباشد (و بنابراین مشخص کنندهٔ شکل V است)؛ به ویژه شیئی از طبقهٔ عملگری FinVctKF(Q) است که (F(Q طبقهٔ آزاد روی Q و تشکیل شده از مسیرهای Q است و FinVctK طبقهٔ فضای برداری با بعد متناهی روی میدان K است. نمایشهای یک quiver رأسهای آن را با فضاهای برداری و یالهایش (و در نتیجه مسیرهایش) را بهطور سازگاری با تبدیلات خطّی بین این فضاها و تبدیل از طریق تبدیلات طبیعی برچسبگذاری میکند.
جستارهای وابسته
پانویس
- «گراف سودار» [ریاضی] همارزِ «directed graph»؛ منبع: گروه واژهگزینی. جواد میرشکاری، ویراستار. دفتر هفتم. فرهنگ واژههای مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۷۸-۹۶۴-۷۵۳۱-۹۴-۸ (ذیل سرواژهٔ گراف سودار)
- Bang-Jensen & Gutin (2000). Diestel (2005), Section 1.10. Bondy & Murty (1976), Section 10.
- Diestel (2005), section 1.10.
- Satyanarayana, Bhavanari; Prasad, Kuncham Syam, Discrete Mathematics and Graph Theory, PHI Learning Pvt. Ltd., p. 460, ISBN 978-81-203-3842-5; Brualdi, Richard A. (2006), Combinatorial matrix classes, Encyclopedia of mathematics and its applications 108, Cambridge University Press, p. 51, ISBN 978-0-521-86565-4.
- Bang-Jensen & Gutin (2000) p. 19 in the 2007 edition; p. 20 in the 2nd edition (2009).
منابع
- Bang-Jensen, Jørgen; Gutin, Gregory (2000), Digraphs: Theory, Algorithms and Applications, Springer, ISBN 1-85233-268-9
(the corrected 1st edition of 2007 is now freely available on the authors' site; the 2nd edition appeared in 2009 ISBN 1-84800-997-6). - Bondy, John Adrian; Murty, U. S. R. (1976), Graph Theory with Applications, North-Holland, ISBN 0-444-19451-7, archived from the original on 13 April 2010, retrieved 22 May 2014.
- Diestel, Reinhard (2005), Graph Theory (3rd ed.), Springer, ISBN 3-540-26182-6 (the electronic 3rd edition is freely available on author's site).
- Harary, Frank; Norman, Robert Z.; Cartwright, Dorwin (1965), Structural Models: An Introduction to the Theory of Directed Graphs, New York: Wiley.
- Number of directed graphs (or digraphs) with n nodes.
