درخت ایویال
الگوریتم علوم رایانه، درخت ایویال (به انگلیسی: AVL tree)، یک نوع درخت جستجوی دودویی خود متوازنکنندهاست و اولین ساختار دادهای از این نوع میباشد که اختراع شد.[1] در یک درخت ایویال اختلاف ارتفاع دو زیر شاخهٔ هر گره حداکثر برابر یک است؛ بنابراین به این درخت، درخت با ارتفاع متوازن نیز گفته میشود. توجه کنید که عملیات درج، حذف و جستجو در یک درخت ایویال در بدترین حالت و حالت متوسط به اندازه خواهد بود بهطوریکه n تعداد گرههای درخت میباشد. در عملیات درج و حذف ممکن است نیاز باشد که درخت به وسیله چرخش درختها، یک یا چند بار متوازن گردد.
| درخت ایویال | ||
|---|---|---|
| نوع | درخت | |
| سال اختراع شدن | ۱۹۶۲ | |
| اختراع شده توسط | جرجی اندلسون-ولسکی و اوگنی لاندیس | |
| پیچیدگی زمانی بر حسب نماد اوی بزرگ | ||
| میانگین | بدترین حالت | |
| فضا | O(n) | O(n) |
| جستجو | O(log n) | O(log n) |
| درج | O(log n) | |
| حذف | O(log n) | O(log n) |
عنوان AVL TREE از اول نامهای دو مخترع آن به نامهای G.M. Adelson-Velsky و E.M. Landis، که مقاله خود را در سال ۱۹۶۲ با موضوع «یک الگوریتم برای سازماندهی اطلاعات» منتشر کردند گرفته شدهاست.
درختهای ایویال غالباً با درختهای قرمز-سیاه مقایسه میشود. دلیل آن این است که هر دو داده ساختار قادر به انجام یک مجموعه از عملیات یکسان میباشند. در درختهای قرمز-سیاه نیز زمان لازم برای انجام عملیات اساسی به اندازه است. درختهای ایویال برای کاربردهای وسیع و گسترده جستجو بهتر از درختهای قرمز-سیاه هستند. الگوریتمهای متوازن کردن درختها در بسیاری از دورههای علوم رایانه ظاهر شده و مورد استفاده قرار میگیرد.[2]

تعریف اولیه
ضریب توازن هر گره، تفاضل ارتفاع زیردرخت چپ آن گره از ارتفاع زیردرخت راست آن گره است. برای راس داریم:
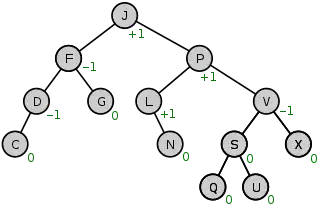
هر گره ای که ضریب توازن آن برابر ۱، ۰ یا ۱- باشد به عنوان گره متوازن در نظر گرفته میشود. هر درخت جستوجوی دودویی که تمام راسهای آن متوازن باشند درخت ایویال است.
با دانستن تعریف یک درخت ایویال و ضریب توازن، با اضافه شدن گره جدید و تغییر ارتفاع، میتوان یک درخت ایویال را متوازن نگه داشت. دقت شود که نیازی به نگه داشتن ارتفاع دقیق هر گره نیست. تنها کافی است برای هر گره ضریب توازن را نگه داریم. در روش قدیمی برای هر گره دو بیت نگه داشته میشد ولی تحقیقات بعدی نشان داد که تنها یک بیت برای هر گره کافی است. به این صورت که برای در هر گره تفاضل ارتفاع گره با از ارتفاع پدرش ذخیره میشود و همانطور که واضح است این مقدار همواره برابر ۱ یا ۲ است. ارتفاع هر درخت ایویال با تعداد n گره همواره در محدوده زیر قرار دارد:
که در آن با تعریف عدد طلایی ، و . دلیل این محدوده این است که هر درخت ایویال با ارتفاع h، حداقل به تعداد Fh+2 – 1 گره دارد که در آن F دنباله فیبوناتچی است.
عملیات

بهطور کلی عملیات اساسی در درختهای ایویال شامل همان عملیاتی که در درختهای جستجوی دودویی انجام میشود میباشد، اما اصلاحات وتغییرات به صورت فراخوانی یک یا چند باره چرخش درخت خواهد بود که به باز ذخیره کردن ارتفاع زیر درخت کمک میکند.
درج کردن
اگر ضریب توازن تمام گرهها ۱-، ۰ یا ۱ باشد درخت در حال حاضر متوازن است و هیچ چرخش دیگری نیاز ندارد.
اگر ضریب توازن یک گره ۲ یا ۲- شود، درخت با ریشه این گره نامتوازن است و چرخش درخت نیاز است. حداکثر دو چرخش برای متوازن کردن درخت نیاز خواهد بود.
چهار حالت اساسی برای محاسبه وجود دارد که دو تای آنها متناسب، یا به عبارت دیگر متقارن با دو حالت دیگر است.
برای سادگی ریشه زیر درخت نامتوازن را P، فرزند سمت راست آن را R، و فرزند سمت چپ را L بنامید. اگر ضریب توازن P مساوی ۲ بود یعنی زیر درخت سمت راست سنگین تر از زیر درخت سمت چپ است و باید ضریب توازن فرزند سمت راست بررسی شود. اگر ضریب توازن (R)برابر ۱ است، این بدان معنا است که درج در سمت راست آن گره رخ داده و یک چرخش درخت به چپ با محوریت ریشه P است. اگر ضریب توازن R برابر ۱- باشد، این بدان معنا است که درج در سمت چپ گره اتفاق افتادهاست. در این حالت نیاز به دو بار چرخش میباشد. اولین چرخش به سمت راست با محوریت R به عنوان ریشه و سپس یک چرخش به سمت چپ با محوریت P است.[4] مراحل کامل متوازن کردن در بخش متوازنسازی توضیح داده خواهد شد.
for (X = parent(Z); X != null; X = parent(Z)) { // Loop (possibly up to the root)
// BalanceFactor(X) has to be updated:
if (Z == right_child(X)) { // The right subtree increases
if (BalanceFactor(X) > 0) { // X is right-heavy
// === > the temporary BalanceFactor(X) == +2
// ===> rebalancing is required.
G = parent(X); // Save parent of X around rotations
if (BalanceFactor(Z) < 0) // Right Left Case (see figure 5)
N = rotate_RightLeft(X, Z); // Double rotation: Right(Z) then Left(X)
else // Right Right Case (see figure 4)
N = rotate_Left(X, Z); // Single rotation Left(X)
// After rotation adapt parent link
} else {
if (BalanceFactor(X) < 0) {
BalanceFactor(X) = 0; // Z’s height increase is absorbed at X.
break; // Leave the loop
}
BalanceFactor(X) = +1;
Z = X; // Height(Z) increases by 1
continue;
}
} else { // Z == left_child(X): the left subtree increases
if (BalanceFactor(X) < 0) { // X is left-heavy
// === > the temporary BalanceFactor(X) == –2
// ===> rebalancing is required.
G = parent(X); // Save parent of X around rotations
if (BalanceFactor(Z) > 0) // Left Right Case
N = rotate_LeftRight(X, Z); // Double rotation: Left(Z) then Right(X)
else // Left Left Case
N = rotate_Right(X, Z); // Single rotation Right(X)
// After rotation adapt parent link
} else {
if (BalanceFactor(X) > 0) {
BalanceFactor(X) = 0; // Z’s height increase is absorbed at X.
break; // Leave the loop
}
BalanceFactor(X) = –1;
Z = X; // Height(Z) increases by 1
continue;
}
}
// After a rotation adapt parent link:
// N is the new root of the rotated subtree
// Height does not change: Height(N) == old Height(X)
parent(N) = G;
if (G != null) {
if (X == left_child(G))
left_child(G) = N;
else
right_child(G) = N;
break;
} else {
tree->root = N; // N is the new root of the total tree
break;
}
// There is no fall thru, only break; or continue;
}
// Unless loop is left via break, the height of the total tree increases by 1.
حذف کردن
اگر گره یک برگ باشد میتوان آن را حذف کرد. در غیر این صورت آن را با بزرگترین گره در زیر درخت سمت چپش یا با کوچکترین گره در زیر درخت سمت راستش جایگزین میکنیم و محل جایگزینی را به خاطر میسپاریم. سپس آن گره را (که حالا حداکثر یک بچه دارد) در محل جایگزینی به راحتی حذف میکنیم. بعد از حذف گره مسیری را که از سمت محل جایگزینی به طرف ریشه است را پیمایش میکنیم و ضریبهای توازن را در صورت لزوم اصلاح میکنیم. (این عمل را بازیابی مسیر مینامیم). اگر در طول مسیر در یک گره ضریب توازن ۲ یا ۲- شود؛ این بدان معنا است که زیر درخت با ریشه آن گره نامتوازن است و برای متوازن شدن نیاز به چرخش میباشد. هزینه صرف شده برای حذف کردن برابر جمع هزینههای لازم برای جستجو و بازیابی مسیر است که هر دو به اندازه میباشد. در نتیجه هزینه لازم برای حذف نیز از مرتبه میباشد. عملیات چرخش در قسمت متوازنسازی توزیح داده شدهاست.
class Node
{
int key, height;
Node left, right;
Node(int d)
{
key = d;
height = 1;
}
}
class AVLTree
{
Node root;
// A utility function to get height of the tree
int height(Node N)
{
if (N == null)
return 0;
return N.height;
}
// A utility function to get maximum of two integers
int max(int a, int b)
{
return (a > b) ? a : b;
}
// A utility function to right rotate subtree rooted with y
// See the diagram given above.
Node rightRotate(Node y)
{
Node x = y.left;
Node T2 = x.right;
// Perform rotation
x.right = y;
y.left = T2;
// Update heights
y.height = max(height(y.left), height(y.right)) + 1;
x.height = max(height(x.left), height(x.right)) + 1;
// Return new root
return x;
}
// A utility function to left rotate subtree rooted with x
// See the diagram given above.
Node leftRotate(Node x)
{
Node y = x.right;
Node T2 = y.left;
// Perform rotation
y.left = x;
x.right = T2;
// Update heights
x.height = max(height(x.left), height(x.right)) + 1;
y.height = max(height(y.left), height(y.right)) + 1;
// Return new root
return y;
}
// Get Balance factor of node N
int getBalance(Node N)
{
if (N == null)
return 0;
return height(N.left) - height(N.right);
}
/* Given a non-empty binary search tree, return the
node with minimum key value found in that tree.
Note that the entire tree does not need to be
searched. */
Node minValueNode(Node node)
{
Node current = node;
/* loop down to find the leftmost leaf */
while (current.left != null)
current = current.left;
return current;
}
Node deleteNode(Node root, int key)
{
// STEP 1: PERFORM STANDARD BST DELETE
if (root == null)
return root;
// If the key to be deleted is smaller than
// the root's key, then it lies in left subtree
if (key < root.key)
root.left = deleteNode(root.left, key);
// If the key to be deleted is greater than the
// root's key, then it lies in right subtree
else if (key > root.key)
root.right = deleteNode(root.right, key);
// if key is same as root's key, then this is the node
// to be deleted
else
{
// node with only one child or no child
if ((root.left == null) || (root.right == null))
{
Node temp = null;
if (temp == root.left)
temp = root.right;
else
temp = root.left;
// No child case
if (temp == null)
{
temp = root;
root = null;
}
else // One child case
root = temp; // Copy the contents of
// the non-empty child
}
else
{
// node with two children: Get the inorder
// successor (smallest in the right subtree)
Node temp = minValueNode(root.right);
// Copy the inorder successor's data to this node
root.key = temp.key;
// Delete the inorder successor
root.right = deleteNode(root.right, temp.key);
}
}
// If the tree had only one node then return
if (root == null)
return root;
// STEP 2: UPDATE HEIGHT OF THE CURRENT NODE
root.height = max(height(root.left), height(root.right)) + 1;
// STEP 3: GET THE BALANCE FACTOR OF THIS NODE (to check whether
// this node became unbalanced)
int balance = getBalance(root);
// If this node becomes unbalanced, then there are 4 cases
// Left Left Case
if (balance > 1 && getBalance(root.left) >= 0)
return rightRotate(root);
// Left Right Case
if (balance > 1 && getBalance(root.left) < 0)
{
root.left = leftRotate(root.left);
return rightRotate(root);
}
// Right Right Case
if (balance < -1 && getBalance(root.right) <= 0)
return leftRotate(root);
// Right Left Case
if (balance < -1 && getBalance(root.right) > 0)
{
root.right = rightRotate(root.right);
return leftRotate(root);
}
return root;
}
جستجو
جستجو در درخت ایویال همانند جستجو در در خت دودویی نامتوازن است. به دلیل توازن ارتفاع درخت هزینه جستجو در بدترین حالت برابر است. هیچ شرط خاصی برای رعایت کردن وجود ندارد و در طول جستجو ساختار درخت تغییری نمیکند. (می توان جستجو در درخت ایویال را در تباین با جستجو در درخت گسترده دانست که در آن ساختار درخت در حین جستجو تغییر میکند) اگر هر گره ارتفاع زیر درخت خود را نیز ذخیره کند، هر گره میتواند در زمان نیز بازیابی شود. گره قبل و بعد هر گره در درخت ایویال در یک زمان ثابت سرشکن قابل دسترسی است. در موارد محدودی حدود پیوند پیمایش میشود. در اکثر موارد یک پیوند و در حالت سرشکن دو پیوند پیمایش میشود.
متوازنسازی
اگر در هنگام اجرای یک عملیات (درج یا حذف) روی یک درخت ایویال ضریب توازن یک گره ۲ یا ۲- شود، (از محدوده مجاز ۱ تا ۱- خارج شود) آن درخت نیازمند عمل متوازنسازی خواهدبود. فرض کنید گره ای که ضریب توازنش از محدوده مجاز خارج شدهاست X و فرزند بزرگتر آن (با ارتفاع بیشتر) Z باشند. توجه شود که میدانیم زیر درخت Z یک درخت ایویال است. علت عدم توازن X در عمل درج، اضافه شدن یک نود به Z، و در عمل حذف، حذف شدن یک نود از بچههای برادر Z است.
اگر فرزندان Z را ZR(فرزند راست) و ZL(فرزند چپ) بنامیم چهار حالت پیش میآید:
- راست راست: Z فرزند راست X باشد و ZL سنگین تر از ZR نباشد.
- چپ چپ: Z فرزند چپ X باشد و ZR سنگین تر از ZL نباشد.
- راست چپ: Z فرزند راست X باشد و ZR سنگین تر از ZL نباشد.
- چپ راست: Z فرزند چپ X باشد و ZL سنگین تر از ZR نباشد.
در دو حالت اول (راست راست و چپ چپ) نیاز به تک-چرخش و در دو حالت دیگر نیاز به دو-چرخش است.
تک چرخش

در شکل مقابل یک نمونه از مشکل راست راست با یک چرخش چپ حل شدهاست.
همانطور که مشاهده میشود با تغییر سه یال و به روز رسانی دو ضریب توازن، این درخت دوباره متوازن شدهاست.
در چرخش چپ، همانطور که ملاحظه میشود، گرههای سمت راست X و چپ Z تغییری نمیکنند. پدر X به جای X به Z وصل میشود. X و Z جایشان را با هم عوض میکنند. (رابطه پدر فرزندی جابجا میشود) و در نهایت فرزند چپ Z به راست X وصل میشود.

یک نمونه کد از چرخش چپ:
node *rotate_Left(node *X, node *Z) {
// Z is by 2 higher than its sibling
t23 = left_child(Z); // Inner child of Z
right_child(X) = t23;
if (t23 != null)
parent(t23) = X;
left_child(Z) = X;
parent(X) = Z;
// 1st case, BalanceFactor(Z) == 0, only happens with deletion, not insertion:
if (BalanceFactor(Z) == 0) { // t23 has been of same height as t4
BalanceFactor(X) = +1; // t23 now higher
BalanceFactor(Z) = –1; // t4 now lower than X
} else { // 2nd case happens with insertion or deletion:
BalanceFactor(X) = 0;
BalanceFactor(Z) = 0;
}
return Z; // return new root of rotated subtree
}
دو چرخش
در شکل مقابل وضیت چپ راست نمایش داده شدهاست.
در این حالت ابتدا با جابحا کردن Y و Z به یکی از حالات چپ چپ یا راست راست میرسیم و سپس با یک چرخش درخت را متوازن میکنیم.
نمونه کد:

ode *rotate_RightLeft(node *X, node *Z) {
// Z is by 2 higher than its sibling
Y = left_child(Z); // Inner child of Z
// Y is by 1 higher than sibling
t3 = right_child(Y);
left_child(Z) = t3;
if (t3 != null)
parent(t3) = Z;
right_child(Y) = Z;
parent(Z) = Y;
t2 = left_child(Y);
right_child(X) = t2;
if (t2 != null)
parent(t2) = X;
left_child(Y) = X;
parent(X) = Y;
// 1st case, BalanceFactor(Y) > 0, happens with insertion or deletion:
if (BalanceFactor(Y) > 0) { // t3 was higher
BalanceFactor(X) = –1; // t1 now higher
BalanceFactor(Z) = 0;
} else // 2nd case, BalanceFactor(Y) == 0, only happens with deletion, not insertion:
if (BalanceFactor(Y) == 0) {
BalanceFactor(X) = 0;
BalanceFactor(Z) = 0;
} else { // 3rd case happens with insertion or deletion:
// t2 was higher
BalanceFactor(X) = 0;
BalanceFactor(Z) = +1; // t4 now higher
}
BalanceFactor(Y) = 0;
return Y; // return new root of rotated subtree
}


مقایسه با ساختارهای دادهٔ دیگر
درختهای ایویال و قرمز-سیاه، هر دو از نوع درختهای جستجوی دودویی خود متوازنکننده هستند، بنابراین از نظر قانون ریاضی تفاوتی ندارند. عملیات برای متوازن کردن آنها متفاوتند اما هر دو در زمان ثابتی انجام میشوند. تفاوت بین آ نها در میزان ارتفاعشان است. برای یک درخت به سایز n:
- ارتفاع درخت ایویال محدود میشود به:
- ارتفاع درخت قرمز-سیاه محدود میشود به:
درخت ایویال دارای توازن بیشتری نسبت به درخت قرمز-سیاهاست یا به عبارت دیگر بسیار متوازن تر از درخت قرمز-سیاهاست، که این منجر به این میشود که حذف و درج کردن به صورت کند، اما بازیابی در زمان سریع تری انجام شود.
جستارهای وابسته
- درختها
- چرخش درخت
- درخت گسترده
- درخت قرمز-سیاه
- درخت بی
- درخت تی
- لیست ساختمانهای داده
منابع
- ویکیپدیای انگلیسی:
- رابرت سدجویک، الگوریتمها، ادیسون-ویسلی، ۱۹۸۳, شابک ۰−۲۰۱−۰۶۶۷۲−۶ ، صفحه ۱۹۹، فصل ۱۵: درختهای متوازن.
- پی فاف، بن (ژوئن ۲۰۰۴)، آنالیز BSTs در سیستمهای نرمافزار (PDF)، دانشگاه استنفورد پیوند خارجی در
|title=وجود دارد (کمک) - 1938-، Knuth, Donald Ervin, (©1973-©1981). The art of computer programming. Reading, Mass.: Addison-Wesley Pub. Co. OCLC 823849. شابک ۰۲۰۱۰۳۸۰۹۹. تاریخ وارد شده در
|تاریخ=را بررسی کنید (کمک) - یوسفی، جواد (۱۳۸۹)، درخت AVL (PDF) پیوند خارجی در
|title=وجود دارد (کمک) - «AVL Tree | Set 2 (Deletion) - GeeksforGeeks» (به انگلیسی). GeeksforGeeks. ۲۰۱۲-۰۳-۱۱. دریافتشده در ۲۰۱۸-۰۶-۰۹.
- Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Pages 458–475 of section 6.2.3: Balanced Trees.
