درخت دودویی
در علوم رایانه، یک درخت دودویی یک ساختمان دادهٔ درخت است که در آن هر گره حداکثر دو گره فرزند دارد که فرزندان راست و چپ نامیده میشوند. در درخت دودویی، در جهٔ هر گره حداکثر میتواند دو باشد. درختهای دودویی برای پیادهسازی درخت جستجوی دودویی و انبوه دودویی و برای جستجوی کارآمد و مرتبسازی استفاده میشود. درخت دودویی یک حالت خاص از یک درخت kتایی است، که در آن k برابر ۲ است.
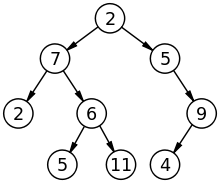
انواع درختان دودویی
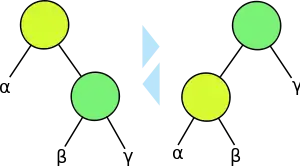
- درخت دودویی ریشهدار یک درخت با یک گره ریشه است که در آن هر گره حداکثر دو فرزند دارد.
- درخت دودویی پر(گاهی اوقات درخت دودویی مناسب یا ۲_ درخت یا درخت اکیداً دودویی گفته میشود) یک درخت که در آن هر گره به غیر از برگها دارای دو فرزند است. هر گره در درخت دودویی دارای دو فرزند یا بدون فرزند است. یک درخت پر گاهی اوقات بهطور ابهامانگیزی به عنوان درخت دودویی کامل تعریف میشود. فیزیکدانان یک درخت دودویی را بهعنوان درخت دودویی پر تعریف میکنند.[1]
 یک تبارنامه که روی یک درخت دودویی کامل به عمق ۴ نگاشت شدهاست
یک تبارنامه که روی یک درخت دودویی کامل به عمق ۴ نگاشت شدهاست - یک درخت دودویی کامل (perfect) یک درخت دودویی پر است که در آن همه برگها دارای عمق یکسان یا همسطح باشند، و در آن هر پدری دارای دو فرزند است.[2](بهطور مبهم درخت دودویی کامل نامیده میشود (بعدی را مشاهده کنید).) نمونهای از یک درخت دودویی کامل را میتوان در تبارنامه از یک فرد به عمق دادهشده مشاهده کرد، بهطوری که هر فرد دقیقاً دو پدر و مادر (یک مادر و یک پدر) دارد؛ توجه داشتهباشید که این معکوس قرارداد معمول درخت پدر\ فرزند است، و این درختان خلاف جهت معمول هستند (ریشه در پایین).
- یک درخت دودویی کامل (complete) یک درخت دودویی است که در آن هر سطح، به جز احتمالاً آخرین سطح، بهطور کامل پر شدهاست، و همهٔ گرهها تا جایی که ممکن است در چپ درخت قرار میگیرند.[3] درختی که این استثناء را داشتهباشد که سطح آخر آن کاملاً پر نباشد، درخت دودویی تقریباً کامل یا نزدیک به درخت دودویی کامل گویند. این نوع درختان از ساختمان دادهٔ ویژهای به نام هیپ استفاده میکنند.
- درخت دودویی کامل نا محدود درختی است که دارای بینهایت سطح قابل شمارش است، که در آن هر گره دارای دو فرزند است بهطوری که گرههای 2d در سطح d هستند. مجموعهٔ گرهها شمارای نامتناهی است، ولی مجموعهای از بینهایت مسیر از ریشه، ناشمارا است، که دارای عدد کاردینالیتی پیوسته است. این مسیرها رابطهٔ دوسویی را با نقاط مجموعه کانتور، یا مجموعهای از اعداد گنگ حفظ میکند.
- درختی دودویی متوازن که معمولاً بهعنوان درخت دودویی است که در آن اختلاف عمق زیردرخت چپ و راست آن ۱ یا کمتر است، اگر چه بهطور کلی درخت دودویی است که هیچ برگی نسبت با برگهای دیگر فاصلهٔ زیادی تا ریشه ندارد. (طرح توازن متمایز اجازه میدهد که تعریف متفاوتی از «بسیار دورتر» ارائه شود) درخت دودویی هنگامی متوازن است که مطابق تعریف عمق آن قابل پیشبینی باشد. (بسیاری از گرهها از ریشه تا برگ پیموده میشوند، چنانکه شمارهٔ ریشه به عنوان گرهٔ ۰ و بقیهٔ گرهها اعداد ۱ ۲ … n را میگیرند) این عمق (ارتفاع هم نامیده میشود) برابر قسمت صحیح (log2(n است، که در آن n تعداد گرهها در درخت متوازن است. مثلاً، برای درخت متوازنی که دارای ۱ گره است، log2(1) = ۰، در نتیجه عمق درخت برابر صفر است. برای یک درخت متوازن با ۱۰۰ گره، log2(100) = ۶٫۶۴، در نتیجه عمق درخت برابر ۶ است.
- درخت منحط درختی است که هر گرهٔ والدین فقط به یک گرهٔ فرزند متصل است. این به این معنی است که عملکرد این درخت مانند رفتار ساختمان دادهٔ لیست پیوندی است.
توجه داشتهباشید که اغلب در ادبیات متفاوتند، به خصوص در رابطه با معنای کلمات «کامل» و «پر».
خواص درخت دودویی
- تعداد n گره در درخت دودویی کامل را میتوان با استفاده از این فرمول بدستآورد :n = 2 h + 1 - ۱ که در آن hارتفاع درخت است.
- تعداد n گره در درخت دودویی با ارتفاع h حداقل برابر n = h + 1 و حداکثر n = 2 h + 1 - ۱ است.
- تعداد برگهای l در درخت دودویی کامل را میتوان با استفاده از این فرمول بدستآورد :l = 2 h که در آن h ارتفاع درخت است.
- تعداد n گره در درخت دودویی کامل را همچنین میتوان با استفاده از این فرمول بدست آورد: n = 2 l - ۱ که در آن l تعداد برگهای درخت است.
- تعداد پیوندهای تهی (گرههای فرزند وجود ندارند) در درخت دودویی کامل با n گره برابر (n + 1) است.
- تعداد گرههای داخلی (گرههای غیر از برگ یا n - l) در درخت دودویی کامل با n گره برابر (floor (n/2 است.
- برای هر درخت دودویی ناتهی با n0 برگ و n2 گره با درجهٔ ۲ داریم :n0 = n2 + 1.[4]
عملیات متداول
انواع عملیاتهای مختلف را میتوان روی درخت دودویی انجام داد. بعضی از عملیاتها تغیری ایجاد میکنند، درحالی که دیگر عملیات اطلاعات مفیدی را در مورد درخت برمیگرداند.
درج
گرهها در درخت دودویی میتوانند بین دو گره دیگر یا بعد از گره خارجی درج شوند. در درخت دودویی گره درج شده به عنوان فرزند مشخص میشود.
گرههای خارجی
گره خارجی اضافه شده گره A است، برای اضافه کردن یک گره بعد از گره A، گره A گره جدید را به عنوان فرزند مشخص خود میکند و گره جدید گره A را به عنوان گره والد تعیین میکند.
گرههای داخلی

درج در گرههای داخلی پیچیدهتر از گرههای خارجی است. فرض میکنیم که A گرهٔ داخلی و B فرزند گرهٔ A باشد. (اگر درج در قسمت فرزند راست باشد، آنگاه B فرزند سمت راست A است، برای درج فرزند سمت چپ هم همینطور است) A فرزند جدید را مشخص میکند و گرهٔ جدید A را که والدین آن است مشخص میکند.
حذف
حذف فرآیندی است که یک گره را از درخت حذف میکند. فقط میتوان گرههای خاصی را در درخت دودویی به وضوح حذف کرد.[5]
گرهٔ بدون فرزند یا دارای یک فرزند

فرض کنید گرهای که میخواهیم حذف کنیم گرهٔ A باشد. اگر گره بدون فرزند باشد (گرۀ خارجی)، آنگاه فرزند والدین گرهٔ A تهی میشود. اگر دارای یک فرزند باشد، آنگاه فرزند A را به والدین گرهٔ A متصل میکنیم در نتیجه والدین فرزند A والدین گرهٔ A میشود.
گره با دو فرزند
در یک درخت دودویی نمیتوان گرهای که دارای دو فرزند است را به وضوح حذف کرد.[5] اگر چه، در درخت دودویی (شامل درخت جستجوی دودویی) این گرهها قابل حذف هستند، ولی با ترمیم ساختمان درخت همراه است.
پیمایش
پیمایشهای پسوندی، میانوندی و پیشوندی پیمایشهایی هستند که به وسیلهٔ آنها میتوان همهٔ گرهها زیردرخت چپ، راست و ریشه را بهطور بازگشتی ملاقات کرد.
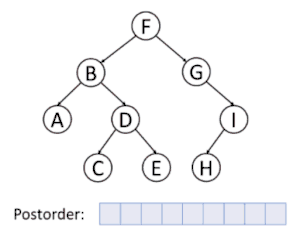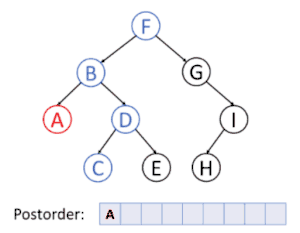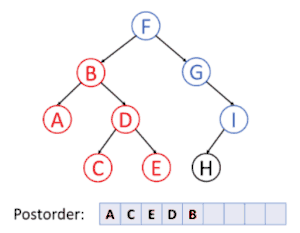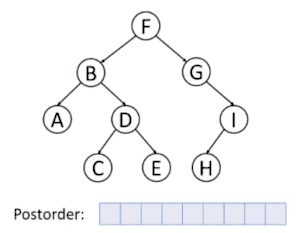
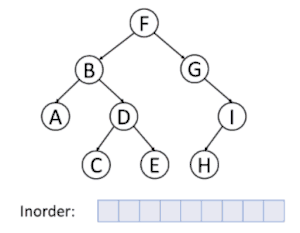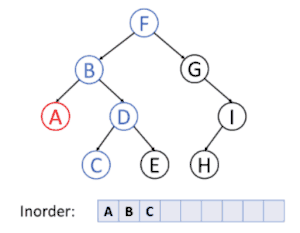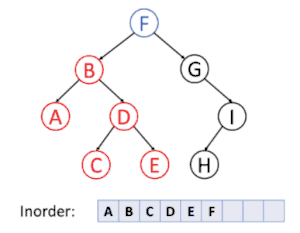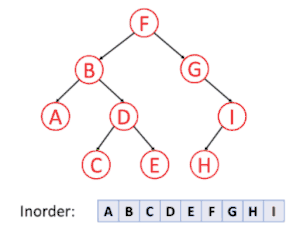
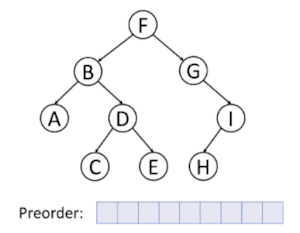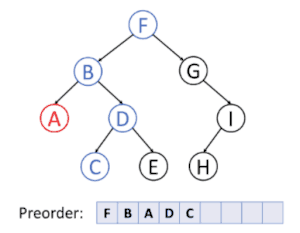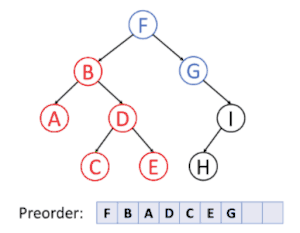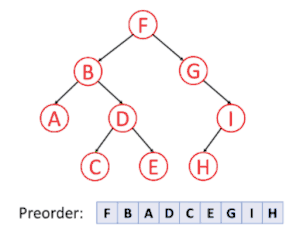
پیمایش عمق نخستین
در پیمایش عمق نخستین، همیشه قصد ما ملاقات دورترین گرهٔ ممکن از گرهٔ ریشه است، ولی با این آگاهی که آن گره باید فرزند گرهای باشد که در حال حاضر ملاقات شدهاست. برعکس در جستجوی عمق نخستین گرافها، احتیاجی به بخاطر سپردن گرههایی که قبلاً ملاقات شدهاند نیست، زیرا یک درخت نمیتواند دارای دور باشد. پیمایش پیشوندی یک مورد خاص آن است. برای اطلاعات بیشتر به الگوریتم جستجوی عمق اول مراجعه کنید.
پیمایش عرض نخستین
پیمایش عرض نخستین در مقایسه با عمق نخستین در این است که در این پیمایش همیشه هدف ما ملاقات نزدیکترین گرهٔ ملاقات نشده به ریشه است. برای اطلاعات بیشتر به الگوریتم جستجوی اول سطح مراجعه کنید.
در یک درخت دودویی کامل، اندیس عرض گره ((i - (2d - 1)) را میتوان به عنوان دستور العمل پیماش از ریشه مورد استفاده قرار داد. با شروع از بیت d-1 از چپ به راست میخوانیم، که d در آن همان فاصلهٔ گره تا ریشه است ((d = floor(log2(i+1)) و در سؤال، گره نباید خود ریشه باشد (d>0). هنگامی که اندیس عرضی گره بیت d-1 باشد، دارای بیت ارزش 0 و1 است یعنی در هر مرحله به طور مرتب چپ یا راست را میپوشاند. فرایند پی در پی با چک کردن بیت بعدی ادامه مییابد تا دیگر بیتی موجود نباشد. سمت راستترین بیت نشاندهندهٔ پیمایش نهایی والدین گرهٔ مورد نظر تا خود گره است.
نظریه نوعها
در نظریه نوعها، در یک درخت دودویی با گرههایی از نوع A، بهصورت استقراء تعریف میشوند: .TA = μα. 1 + A × α × α
تعاریف در نظریه گراف
برای هر ساختمان دادهٔ درخت دودویی، ریشه در درخت دودویی معادل ریشه در نظریهٔ گراف است. در نظریههای گراف از تعاریف استفاده میشود: درخت دودویی گرافی همبند بدون دور است که درجهٔ هر رأس آن حداکثر سه است، که آن میتواند هر درخت دودویی با دو یا چند گره را نمایش دهد، دقیقاً بهازای هر گرهٔ درجه سه دو یا بیشتر گرهٔ درجهٔ یک وجود دارد، ولی دارای هر تعداد از گرهٔ درجه دو است. درخت دودویی ریشهدار مانند گرافی است که درجهٔ یکی از رئوس آن بیش از دو نیست در واقع بیش از دو گرهٔ تنها ندارد؛ بنابراین به وسیلهٔ ریشه، انتخاب هر رأس به عنوان والدین و دو فرزند آن منحصربهفرد تعریف شدهاست، با این حال، اطلاعات کافی برای تشخیص فرزند چپ یا راست وجود دارد. اگر ما به ارتباط کمتری نیاز داشتهباشیم گراف این امکان را به ما میدهد که از مؤلفههای همبندی استفاده کنیم. ما به چنین ساختاری جنگل میگوییم. راه دیگر تعریف درخت دودویی، تعریف بازگشتی روی گرافهای مستقیم است.
- یک رأس تک
- یک گراف از دو درخت دودویی تشکیل میشود، به این صورت که یک رأس و یک یال مستقیم اضافه میشود، که آن یال رأس جدید را به ریشهٔ هر کدام از درخت دودویی متصل میکند.
بعلاوه این راه طرز رسیدن به فرزندان را تعین نمیکند، ولی جای خاص ریشه را درست میکند.
روشهای ذخیرهسازی درختان دودویی
درختان دودویی را میتوان با راههای متفاوتی به وسیلهٔ زبان برنامهنویسی اولیه ایجاد کرد.
گرهها و مراجع
در یک زبان با سوابق و منابع، درختان دودویی معمولاً به وسیلهٔ یک ساختار گرهٔ درخت که حاوی برخی دادهها و مراجع در فرزند چپ و راست آن است ساخته میشوند. گاهی اوقات آن گره نیز حاوی یک مرجع به والدین منحصربهفرد خود است. اگر یک گره کمتر از دو فرزند داشتهباشد، ممکن است برخی اشارهگرهای فرزندان ارزش تهی خاصی را قرار دهند، یا اشارهگرها به گرۀ نگهبان خاصی اشاره کنند. در زبانهای برنامهنویسی با اجتماع برچسبها مانند زبان ML، یک گرهٔ درخت معمولاً از اجتماع برچسب دو نوع گره است، که یکی از آنها دارای دادهای ۳تایی، فرزند چپ و فرزند راست، و یکی دیگر از آنها گرهٔ برگ است، که شامل هیچ داده و تابعی ناست مانند ساختن مقدار تهی به وسیلهٔ اشارهگرها در زبان برنامهنویسی.
آرایهها
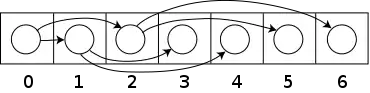
درختان دودویی نیز میتوانند با پیمایش عرض نخستین مانند ساختمان دادۀ مجازی در آرایهها ذخیره شوند، و اگر درخت دودویی کامل باشد در این روش هیچ فاصلهٔ زائدی ایجاد نمیشود. بهطور خلاصه، اگر گرهای دارای اندیس i باشد، آنگاه اندیس فرزند چپ آن و اندیس فرزند راست آن میشود، حال با داشتن اندیس هر کدام از فرزندان اندیس والدین به صورت بدست میآید (با فرض اینکه اندیس ریشه صفر باشد). در این روش هر چه ذخیرهسازی فشردهتر باشد و محل ارجاع بهتر باشد مفیدتر است، بهخصوص در پیماش پیشوندی. اگرچه، رشد کردن درخت دارای هزینه است، که این فاصلهٔ زائد متناسب با h - n>2 است که در آن h عمق درخت و n تعداد گرهها است. این روش ذخیرهسازی معمولاً برای هرم دودویی استفاده میشود، و هیچ فضایی ازبین نمیرود چون گرهها به صورت عرض نخستین اضافه میشوند.
سیستمهای کدگذاری
کدگذاری فشرده
داده ساختارهای فشرده که فضای اشغال شده را تا حد ممکن کوچک میکند، و به عنوان کران پایین در نظریه اطلاعات تأسیس شدهاست. تعداد درختان دودویی متفاوت روی گره است. روی اعداد کاتالان است (با فرض اینکه ما درختان با ساختار یکسان را مشابه مشاهده میکنیم) برای بزرگ آن برابر است؛ به این ترتیب ما به حداقل آن نیاز داریم که تقریباً برابر بیت در کدگذاری آن است؛ بنابراین یک درخت دودویی فضا را اشغال میکند. یک نمایش ساده برای ملاقات گرههای درخت در پیمایش پیشوندی این است که خروجی عدد "۱" نشاندهندهٔ گرهٔ داخلی و عدد " ۰" نشاندهندهٔ برگ است. اگر درخت شامل داده باشد، میتوانیم به سادگی بهطور همزمان دادهها را با پیمایش پیشوندی در آرایههای پیدرپی ذخیره کنیم. تابع مورد نظر به صورت زیر است:
function EncodeSuccinct(node n, bitstring structure, array data) {
if n = nil then
append 0 to structure;
else
append 1 to structure;
append n.data to data;
EncodeSuccinct(n.left, structure, data);
EncodeSuccinct(n.right, structure, data);
}
در پایان ساختار رشتهای فقط دارای بیت است، که n در آن تعداد گرههای داخلی است؛ ما هیچ وقت عمق را ذخیره نمیکنیم. این نشان میدهد که هیچ اطلاعاتی از دست نمیرود، ما میتوانیم بااستفاده از کد زیر خروجی را به درخت اصلی تبدیل کنیم:
function DecodeSuccinct(bitstring structure, array data) {
remove first bit of structure and put it in b
if b = 1 then
create a new node n
remove first element of data and put it in n.data
n.left = DecodeSuccinct(structure, data)
n.right = DecodeSuccinct(structure, data)
return n
else
return nil
}
کدگذاری درختان معمولی به عنوان درخت دودویی
یک نگاشت یک به یک بین مدل معمولی درختان و درختان دودویی وجود دارد؛ که معمولاً این تبدیل توسط زبان لیسپ انجام میشود. برای تبدیل درخت معمولی به مدل معمولی آن، تنها نیاز داریم که مسیر فرزندان درخت معمولی را نشان دهیم، در نتیجه درخت بهطور خودکار به درخت دودویی تبدیل میشود. هر گره مانند N در درخت مورد نظر با گرهٔ 'N در درخت دودویی با هم رابطه دارند بهطوری که: فرزند چپ 'N همان اولین فرزند گرهٔ N است، و فرزند راست 'N همان برادر (خواهر) گرهٔ N است، گرهٔ بعدی از میان فرزندانی است که والدین آنها N است. این درخت دودویی، درخت بررسی شده معمولی را نشان میدهد که گاهی اوقات نیز به درخت دودویی فرزند-چپ همزاد- راست (درخت LCRS) یا درخت مضاعف زنجیر وار یا زنجیر ارث بری فرزندان مقایسه میکند. یکی از راههای فکر کردن در این مورد این است که هر یک از گرههای فرزند در (لیست پیوندی) قرار گیرند. برای مثال، در درخت سمت چپ، A دارای ۶ فرزند است {B,C,D,E,F,G}، که میتوان این درخت را به درخت دودویی سمت راست تبدیل کرد.
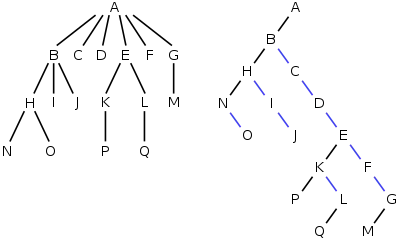
درخت دودویی را میتوان به مدل اصلی خودش برگرداند، گرهٔ متصل به یال سیاه رنگ سمت چپ نشاندهندهٔ فرزند اول آن است و گرههای متصل به یالهای آبی رنگ سمت راست آن نشاندهندهٔ برادر (خواهر) آن است. برگهای آن در سمت چپ قرار دارد که در لیسپ به صورت زیر است: (((N O) I J) C D ((P)(Q)) F (M))
جستارهای وابسته
- درخت ۲–۳
- درخت ۲–۳-۴
- درخت آآ
- Ahnentafel
- درخت ایویال
- درخت بی
- تقسیمبندی فضای دودویی
- کدگذاری هافمن
- درخت K آرایهای
- نامساوی کرافتس
- درخت جستجوی دودویی بهینه
- درخت دودویی تصادفی
- توابع بازگشتی
- درخت سرخ-سیاه
- طناب (ساختمان داده)
- درخت جستجوی دودویی خود-متوازن
- درخت اسپلی
- رتبهبندی استرالر
- درخت سه گانۀ فیثاغورثی اولیه
- درخت دودویی بدون ریشه
منابع
- Unitary Symmetry, James D. Louck, World Scientific Pub. , 2008
- "perfect binary tree". NIST.
- "complete binary tree". NIST.
- Mehta, Dinesh (2004). Handbook of Data Structures and Applications. Chapman and Hall. ISBN 1-58488-435-5. Unknown parameter
|coauthors=ignored (|author=suggested) (help) - Dung X. Nguyen (2003). "Binary Tree Structure". rice.edu. Retrieved December 28, 2010.
- Donald Knuth. The art of computer programming vol 1. Fundamental Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89683-4. Section 2.3, especially subsections 2.3.1–2.3.2 (pp. 318–۳۴۸).
- Kenneth A Berman, Jerome L Paul. Algorithms: Parallel, Sequential and Distributed. Course Technology, 2005. ISBN 0-534-42057-5. Chapter 4. (pp. 113–۱۶۶).
