درخت بی
در علوم کامپیوتر، یک درخت بی یا بیتری (به انگلیسی: B-tree) دادهساختاری درختی است که دادهها را به صورت مرتبشده نگه میدارد و جستجو، درج و حذف را در زمان مصرفی لگاریتمی میسر میسازد. بر خلاف درختهای جستجوی دودویی متوازن (به انگلیسی: Balanced binary search tree)، این دادهساختار برای سیستمهایی که بلاکهای عظیم اطلاعات را خوانده و مینویسند بهینهسازی شدهاست. این دادهساختار معمولاً در پایگاههای داده و سیستم پرونده استفاده میشود.
| ویرایش درخت بی | ||
|---|---|---|
| نوع | درخت | |
| سال اختراع شدن | ۱۹۷۲ | |
| اختراع شده توسط | رودلف بایر، ادوارد مککریت | |
| پیچیدگی زمانی بر حسب نماد اوی بزرگ | ||
| میانگین | بدترین حالت | |
| فضا | O(n) | O(n) |
| جستجو | O(log n) | O(log n) |
| درج | O(log n) | O(log n) |
| حذف | O(log n) | O(log n) |

در درخت بی، گرههای درونی (و نه برگها) میتوانند یک شمارهٔ متغیر از محدودهای ازپیشتعریفشده مربوط به گرههای فرزند را اختیار کنند. زمانی که دادهها درج شده یا از یک گره حذف میشوند، شمارهٔ گرههای فرزند آنها تغییر میکند. به منظور نگهداری محدودهٔ ازپیشتعریفشده، ممکن است گرههای درونی به هم متصل شده یا از هم جدا شوند. به دلیل اینکه محدودهای از گرههای فرزند مجاز هستند، درخت بی، همانند دیگر درختهای جستجوی متوازن، نیازی ندارد که به صورت متناوب اقدام به برقراری توازن کند، اما به دلیل اینکه گرهها کاملاً پر نیستند، ممکن است مقداری حافظه هدر رود. حدود بالا و پایین شمارهٔ گرههای فرزند، برای یک پیادهسازی خاص، بهطور خاص تعیین شدهاند. برای مثال در یک درخت بیِ ۳–۲ (غالباً تنها با عنوان درخت ۳-۲ مورد اشاره قرار میگیرد)، هر گره ممکن است تنها ۲ یا ۳ گرهٔ فرزند داشتهباشد.
یک درخت بی با استلزام اینکه همهٔ برگها در یک عمق قرار داشته باشند، به صورت متوازن نگه داشتهمیشود. این عمق از طریق عناصری که به درخت اضافه میشوند کمکم افزایش مییابد، ولی افزایش در عمق سراسری، کم اتفاق میافتد و وجود یک گرهٔ اضافیِ دورتر از ریشه را نتیجه میدهد.
درختهای بی، هنگامی که زمان دسترسی به گرهها به میزان قابل توجهی بیشتر از زمان پیمایش بین دو گره باشد، مزیتهایی اساسی بر دیگر انواع پیادهسازی دارند. این اتفاق معمولاً زمانی رخ میدهد که گرهها در حافظهای ثانویه مانند دیسک سخت قرار دارند. به واسطهٔ بییشینه نمودن تعداد فرزندانِ هر گرهٔ درونی، ارتفاع درخت افزایش مییابد، توازن کمتر رخ میدهد، و کارایی بالا میرود. معمولاً این مقدار طوری تنظیم میشود که هر گره، یک بلاک کامل از دیسک یا مقداری برابر از حافظهٔ ثانویه را اشغال کند. هنگامی که درختهای بیِ ۳–۲ ممکن است در حافظهٔ اصلی مفید واقع شوند، اگر اندازهٔ گرهها به اندازهٔ یک بلاک دیسک تنظیم شوند، نتیجه ممکن است، یک درخت بیِ ۵۱۳–۲۵۷ باشد (که در آن اندازهها از توانهای بزرگتر ۲ هستند). یک درخت بی از مرتبهٔ m (بیشینهٔ تعداد فرزندان هر گره) درختی است که خصوصیات زیر را برآورده میکند:
- هر گره حداکثر m فرزند دارد.
- هر گره (به جز ریشه و برگها) حداقل m/2 فرزند دارد.
- ریشه، در صورتی که برگ نباشد، حداقل دو فرزند دارد.
- همهٔ برگها در یک سطح ظاهر شده و اطلاعات را منتقل میکنند.
- گرهای که برگ نبوده و k فرزند داشتهباشد، حاوی k-1 کلید میباشد.
رودالف بیر و دد مککرِیت درخت بی را زمانی که در شرکت بوئینگ،[1] مشغول به کار بودند ابداع نمودند، اما حرف B واقعاً از کجا آمده؟ داگلاس کامر یک سری از احتمالات را پیشنهاد کرد:
- "Balanced," "Broad," یا "Bushy" ممکن است استفاده شدهباشند [چون همهٔ برگها در یک سطح قرار دارند]. دیگران اظهار داشتند که حرف "B" از کلمهٔ بوئینگ گرفته شده است [به این دلیل که پدیدآوردنده درسال ۱۹۷۲ در آزمایشگاههای تحقیقاتی علمی شرکت بوئینگ کار میکرد]. با این وجود پنداشتن درخت بی به عنوان درخت "بِیِر" نیز درخور است.[2]
ساختارهای گره
عناصر هر گرهٔ درونی به عنوان مقادیری که زیردرختهای آن را تقسیم میکند، عمل میکنند. به عنوان مثال، اگر یک گرهٔ درونی سه فرزند (یا زیر درخت) داشته باشند، آنگاه این گره باید دو مقدار یا عنصر جداییِ a1 و a2 داشته باشد. همهٔ مقادیر زیردرخت چپ کمتر از a1، همهٔ مقادیر زیردرخت وسطی بین مقادیر a1 و a2، و همهٔ مقادیر زیردرخت راست بزرگتر از a2 خواهد بود.
گرههای درونی—نه برگها—در یک درخت بی معمولاً به عنوان نمایندهٔ مجموعهٔ مرتبی از عناصر و اشارهگرهای فرزندان در نظر گرفته میشوند. هر گرهٔ درونی شامل یک بیشینه از U فرزند بوده و به جز ریشه، همگی یک کمینه از L فرزند دارند. برای همهٔ گرههای درونی به جز ریشه، تعداد عناصر، یکی کمتر تعداد اشارهگرهای فرزندان میباشد؛ تعداد عناصر بین L-1 و U-1. میباشد. مقدار U باید 2L یا 2L-۱ باشد؛ بنابراین هر گرهٔ درونی حداقل نیمهپر است. این رابطه بین U و L ایجاب میکند که دو گرهٔ نیمهپر بتوانند به منظور ایجاد یک گرهٔ مطلوب به هم وصل شوند، و یک گرهٔ کامل بتواند به دو گرهٔ مطلوب منشعب شود. این ویژگیها، حذف و درج مقادیر جدید را در یک درخت بی ممکن میسازد و امکان حفظ ویژگیهای درخت بی را به درخت میدهد. برگها نیز همین شرایط را برای تعداد عناصر دارند، با این تفاوت که نه فرزندی دارند و نه اشارهگر فرزند.
ریشه، برای تعداد فرزندان، کران بالا دارد، ولی کران پایین نه. برای مثال، وقتی در کل کمتر از L-1 عنصر داشته باشیم، ریشه تنها گرهٔ درخت خواهد بود، و در عین حال فرزندی هم نخواهد داشت. یک درخت بی با عمق n+1 میتواند همانند بک درخت بی با عمق n حدود U، عنصر را ذخیره کند، ولی هزینهٔ عملیات جستجو، درج و حذف با عمق درخت افزایش مییابد. به مثابه یک درخت متوازن، هزینه خیلی آهستهتر از تعداد عناصر افزایش مییابد. بعضی از درختهای متوازن مقادیر را فقط در برگها ذخیره میکنند، و بدین ترتیب انواع مختلف برگها و گرههای درونی را خواهند داشت. درختِ بی، مقادیر را در همهٔ گرهها نگه میدارد، و ممکن است ساختار مشابهی را برای تمام گرهها به کار ببندد. با این وجود، به این دلیل که برگها فرزندی ندارند، یک ساختار اختصاصی برای برگها در درختِ بی، کارایی را بهبود خواهد بخشید.
ارتفاع بهترین حالت و بدترین حالت
ارتفاع بهترین حالتِ یک درخت بی برابر است با:
و ارتفاع بدترین حالت یک درخت بی برابر است با:
که M بیشینهٔ تعداد فرزندانی است که یک گره میتواند داشته باشد.
الگوریتمها
جستجو
همانند چیزی که در یک درخت جستجوی دودویی داریم، جستجو به روش استاندارد انجام میشود. با شروع از ریشه و پیمایش از بالا به پایین، اشارهگرِ فرزندی که مقادیرِ جداییِ آن روی هریک از مقادیری که در حال جستجو شدن هستند، انتخاب میشود. جستجوی دودویی، بهطور نمونه (و نه الزاماً) به منظور یافتن مقادیرِ جدایی و درخت فرزند مورد نظر در داخل گرهها استفاده میشود.
درج
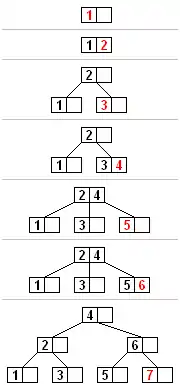
تمامی درجها در برگها انجام میشود.
- از طریق جستجوی درخت، برگی که عنصر جدید باید در آنجا اضافه گردد را مییابیم.
- اگر این برگ، کمتر از بیشینهٔ تعداد قابل قبول، عنصر داشت، برای یکی بیشتر فضا وجود دارد. با مرتب نگهداشتن عناصر گره، عنصر جدید را در این برگ درج میکنیم.
- در غیراینصورت، برگ مورد نظر را به دو گره تقسیم میکنیم.
- میانهٔ منحصربهفرد از بین عناصر برگ و عنصر جدید انتخاب میشود.
- میانه به عنوان مقدار جدایی عمل میکند و مقادیر کمتر از میانه در گرهٔ چپ جدید و مقادیر بزرگتر از میانه در گرهٔ راست جدید قرار داده میشوند.
- این مقدارِ جدایی به گرهٔ پدر اضافه میشود، که این کار ممکن است باعث تقسیم شدن پدر شود، و این روند به همین ترتیب ادامه مییابد.
اگر این تقسیم شدنها تا ریشه ادامه یابد، ریشهٔ جدیدی با یک مقدارِ جدایی یکتا و دو فرزند ایجاد میکند و دلیل اینکه حد پایین برای اندازهٔ گرههای درونی برای ریشه اعمال نمیشود نیز همین میباشد. بیشینهٔ تعداد عناصر در یک گره U-1 میباشد. زمانی که گرهای تقسیم میشود، یک عنصر به پدر انتقال مییابد، ولی یک عنصر هم اضافه میشود؛ بنابراین، باید امکانپذیر باشد که بیشینهٔ تعداد عناصر (U-1) به دو گرهٔ مجاز تقسیم شود. اگر این عدد فرد باشد، آنگاه U=2L بوده و یکی از گرههای جدید شامل U-2)/2 = L-1) عنصر و از اینرو یک گرهٔ مجاز خواهد بود. دیگری هم که یک عنصر بیشتر دارد و از اینرو گرهای مجاز خواهد بود. اگر U-1 زوج باشد، آنگاه U=2L-۱، بوده و لذا 2L-۲ عنصر در گره وجود دارد. نصف این عدد L-1میباشد که کمینهٔ تعداد عناصری است که میتواند در هر گره وجود داشتهباشد.
یک الگوریتم بهبودیافته، بر پایهٔ پیمایشی منفرد به سمت پایین از ریشه به گرهای که قرار است عمل درج در آن انجام شود و تقسیم کردن هر گرهٔ کاملی که در این مسیر با آن مواجه میشود، استوار است. این الگوریتم از نیاز به فراخوانی مجدد پدر به داخل حافظه جلوگیری به عمل میآورد، که این فراخوانی در صورتی که گرهها در حافظهٔ ثانویه قرار داشتهباشند ممکن است پرهزینه باشد. به هرحال، برای استفاده از این الگوریتم بهبودیافته، ما باید قادر باشیم بدون افزودن یک عنصر جدید، عنصری را به پدر منتقل کنیم و U-2 عنصر باقیمانده را به دو گرهٔ قابل قبول تقسیم نماییم. این امر مستلزم آن است که به جای U = 2L داشته باشیم: U = 2L-۱، که به عنوان دلیل بعضی از کتب درسی در قرار دادن این استلزام در تعریف درخت بی، بهشمار میرود.
حذف
دو راهبرد معروف برای حذف از یک درخت بی وجود دارد.
- مکانیابی و حذف عنصر مورد نظر و سپس بازسازی درخت به منظور بازیابی ویژگیهای آن.
یا
- انجام یک پیمایش به سمت پایین در درخت؛ با این تفاوت که پیش از مشاهدهٔ یک گره، درخت را بازسازی میکنیم تا فقط یک بار با کلیدی که قرار است حذف شود برخورد کنیم. بدین ترتیب این عنصر میتواند بدون نیاز به بازسازی بیشتر حذف شود.
الگوریتم زیر از راهبرد اخیر استفاده میکند.
دو مورد خاص وجود دارند که به هنگام حذف یک عنصر باید در نظر گرفته شوند:
- عنصری که در یک گرهٔ درونی قرار دارد ممکن است یک جداکننده برای فرزندانش باشد.
- حذف یک عنصر، ممکن است آن را کمتر از کمینهٔ تعداد عناصر و فرزندان قرار دهد.
هرکدام از این موارد با مرتبهٔ درخت سروکار دارند.
حذف از یک برگ
- جستجوی عنصر به منظور حذف.
- اگر عنصر در یک برگ قرار داشتهباشد، میتواند به آسانی از گره حذف شود. ممکن است با این کار تعداد خیلی کمی عنصر در گره بماند؛ لذا یک سری تغییرات اضافی در درخت لازم است.
حذف از یک گرهٔ درونی
هر عنصر در یک گرهٔ درونی به عنوان یک مقدار جدایی برای دو زیردرخت عمل میکند، و وقتی عنصری حذف میشود، دو حالت رخ میدهد. حالت اول اینکه، هردو فرزندِ راستی و چپیِ عنصری که حذف شده، کمترین تعداد عناصر را دارند یعنی L-1. آنها میتوانند در یک گره با 2L-۲ عنصر به هم بپیوندند، این عدد از تجاوز نمیکند و لذا گرهٔ حاصل، یک گرهٔ قابل قبول خواهد بود. تا زمانی که مطمئن شویم این درختِ بی، دادههای تکراری ندارد، باید بهطور تکراری، با تحقیق در گرهٔ جدید، در صورت وجود عنصر مورد نظر در آن، آن عنصر را حذف کنیم.
حالت دوم اینکه، یکی از دو فرزند، حاوی تعداد بیشتری از کمینهٔ تعداد عناصر میباشد. پس یک جداکنندهٔ جدید باید برای آن زیردرختها یافت شود. توجه داشته باشید که بزرگترین عنصر در زیردرخت چپ، بزرگترین عنصری است که از جداکننده کوچکتر میباشد. به همین ترتیب، کوچکترین عنصردر زیردرخت راست، کوچکترین عنصریاست که از جداکننده بزرگتر میباشد. هر دوی این عناصر در برگ قرار دارند، و هرکدام میتوانند جداکنندهٔ جدیدی برای دو زیردرخت باشند.
- اگر عنصر در یک گرهٔ درونی قرار داشتهباشد، یک جداکنندهٔ جدید انتخاب میکنیم (چه بزرگترین عنصر در زیردرخت چپ باشد، چه کوچکترین عنصر در زیردرخت راست)، آن را از برگی که در آن قرار دارد حذف میکنیم، و عنصری که قرار است حذف شود را با جداکنندهٔ جدید جایگزین میکنیم.
- این کار عنصری را از برگ حذف کردهاست، و لذا همانند حالت قبلی است.
برقراری مجدد توازن بعد از حذف
اگر حذف یک عنصر از برگ، منجر به کمتر شدن آن از کمینهٔ اندازه شود، بعضی از عناصر باید به منظور رساندن تمامی گرهها به کمینه، مجدداً توزیع شوند. در بعضی موارد، این ترتیب دادن مجدد باعث انتقال کاستی به پدر خواهدشد، و لذا توزیع مذکور باید مکرراً به سمت بالای درخت اعمال شود، شاید حتی تا ریشه. از آنجایی که کمینهٔ تعداد عناصر برای ریشه اعمال نمیشود، اینکه ریشه تنها گرهٔ دارای کمبود باشد، مشکلی ایجاد نمیکند. الگوریتم برقراری مجدد توازن درخت در زیر آمده است:
- اگر همزاد راست بیشتر از کمینهٔ تعداد عناصر، عنصر داشت؛
- جداکننده را به انتهای گرهٔ ناقص اضافه میکنیم.
- جداکننده در پدر را با اولین عنصر همزاد راست جایگزین میکنیم.
- اولین فرزندِ همزادِ راست را به آخرین فرزند گرهٔ ناقص وارد میکنیم.
- درغیر اینصورت، اگر همزاد چپ، بیشتر از کمینهٔ تعداد عناصر، عنصر داشت؛
- جداکننده را به ابتدای گرهٔ ناقص اضافه میکنیم.
- جداکننده در پدر را با آخرین عنصر همزاد چپ جایگزین میکنیم.
- آخرین فرزندِ همزادِ چپ را به اولین فرزند گرهٔ ناقص وارد میکنیم.
- اگر هردوی فرزندانِ بدون واسطه، فقط کمینهٔ تعداد عناصر را داشتهباشند؛
- یک گرهٔ جدید با همهٔ عناصرِ گرهٔ ناقص و همهٔ عناصر یکی از همزادان آن و جداکنندهٔ بین دو گرهٔ همزاد مرکب موجود در پدر، میسازیم.
- جداکننده را از پدر حذف میکنیم، و دو فرزندِ حاصله از آن را با گرهٔ ترکیبشده جایگزین میکنیم.
- اگر این کار تعداد عناصر گرهٔ پدر را به زیر مقدار کیمینه رساند، مراحل مذکور را برای آن گرهٔ ناقص هم تکرار میکنیم، مگر زمانی که به ریشه رسیدهباشیم، چرا که ناقص بودن ریشه اشکالی ندارد.
یک حالت دیگر ممکن است رخ دهد و آن زمانی است که ریشه هیچ عنصری نداشته و فقط یک فرزند دارد. در این حالت کافی است ریشه را با تنها فرزندش جایگزین نماییم.
ساختمان اولیه
در کاربردهای مختلف، بارها پیش میآید که ایجاد یک درختِ بی، برای نشان دادن مجموعهٔ وسیعی از اطلاعات و سپس بهروزرسانی آن با استفاده از قابلیتهای درخت بی، سودمند واقع میشود. در این موارد، برای ایجاد درخت بیِ اولیه، درج پیدرپیِ تکتک عناصر مجموعهٔ اولیه، کارآمدترین روش نمیباشد، بلکه به جای آن باید دستهٔ اولیهٔ برگها را مستقیماً از ورودی بسازیم، و سپس گرههای درونی را از آنها تولید کنیم. این روش ایجاد درخت بی، بارگذاریِتنه (bulkloading) نامیده میشود. در ابتدا، تمامی برگها به جز آخرینِ آنها یک عنصرِ اضافه دارد، که برای ایجاد گرههای درونی استفاده خواهد شد.
برای مثال، اگر بیشنهٔ اندازهٔ برگها ۴ باشد و مجموعهٔ اولیه، اعداد صحیح بین ۱ تا ۲۴ باشد، ما باید در ابتدا ۵ برگ که هر کدام به جز آخرینِ آنها حاوی ۵ مقدار است بسازیم (آخرین برگ حاوی ۴ مقدار میباشد):
|
|
|
|
|
ما یک سطح بالاتر از برگها را از طریق برداشتن آخرین عنصر از هر برگ (به جز آخرینِ آنها)، میسازیم. دو مرتبه، هر گره به جز آخرینِ آنها، یک مقدارِ اضافه خواهد داشت. در مثال فوق، فرض کنید گرههای درونی حاوی حداکثر ۲ مقدار باشند (۳ اشارهگر فرزند). آنگاه یک سطحِ گرههای درونیِ بالاتر به ترتیب زیر خواهد بود:
|
|
|
|
|
|
|
این فرایند تا زمانی که به یک سطح با تنها یک گره برسیم که سرریز هم نکرده باشد، ادامه مییابد. در این مثال فقط ریشه باقی میماند:
|
|
|
|
|
|
|
|
منابع
Original papers:
- R. Bayer, Binary B-Trees for Virtual Memory, Proceedings of 1971 ACM-SIGFIDET Workshop on Data Description, Access and Control, San Diego, California, November 11-12, 1971.
- R. Bayer and E. McCreight, ORGANIZATION AND MAINTENANCE OF LARGE ORDERED INDICES, Mathematical and Information Sciences Report No. 20, Mathematical and Information Sciences Laboratory, BOEING SCIENTIFIC RESEARCH LABORATORIES, July 1970.
Summary:
- دانلد کنوت. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Section 6.2.4: Multiway Trees, pp. 481–491. Also, pp. 476–477 of section 6.2.3 (Balanced Trees) discusses 2-3 trees.
- توماس اچ کورمن، Charles E. Leiserson, رونالد ریوست، and کلیفورد استین. مقدمهای بر الگوریتمها, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Chapter 18: B-Trees, pp. 434–454.
Other
- «R. Bayer, E. McCreight. Organization and Maintenance of Large Ordered Indexes, in Acta Informatica, Vol. 1, Fasc. 3, 1972 pp. 173-189» (PDF). بایگانیشده از اصلی (PDF) در ۲۷ دسامبر ۲۰۰۴. دریافتشده در ۱۰ مه ۲۰۰۹.
- Douglas Comer. The Ubiquitous B-Tree. Computing Surveys, 11(2):123. June 1979.
پیوند به بیرون
- B-tree and UB-tree on Scholarpedia Curator: Dr Rudolf Bayer
- B-Tree Applet by Kubo Kovac
- B-Trees: Balanced Tree Data Structures
- NIST's Dictionary of Algorithms and Data Structures: B-tree
- C++ source code for a balanced tree (B-tree) (Windows required for test timings)
- WB disk-based B-tree C-library/Java-library/C#-library
- B-Trees in Perl
