منحنی بزیه
منحنی بزیه (انگلیسی: Bézier curve) نوعی منحنی پارامتری مورد استفاده در گرافیک رایانهای و صنایع مربوطه است. تعمیمهای منحنی بزیه به ابعاد بالاتر را سطوح بزیه مینامند که یکی از حالتهای خاص آنها، مثلث بزیه است.
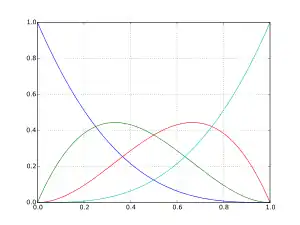
آبی: y = (۱ − t)3،
سبز: y= ۳(۱ − t)2 t،
قرمز: y= ۳(۱ − t) t2، و
نیلی: y = t3.
در گرافیک برداری، از منحنیهای بزیه برای مدلسازی منحنیهای نرمی که میتوانند تا بینهایت بزرگ و کوچک شوند استفاده میشود. از پیوند زدن چند منحنی بزیه ساده یک مسیر (به انگلیسی: path) (منحنی بزیهٔ پیچیده) حاصل میشود. مسیرها تابع محدودیتهای تصویری گرافیک شطرنجی نیستند و کار با آنها از نظر شهودی آسان است.
بنیاد ریاضیاتی منحنیهای بزیه یعنی چندجملهایهای برنشتاین از سال ۱۹۱۲ شناخته شده بود، ولی از این چندجملهای تا حدود ۵۰ سال بعد از آن در گرافیک استفادهای نشد، تا اینکه مهندس فرانسوی پیر بزیه برای طراحی بدنهٔ خودروهای رنو از آن بهره برد.
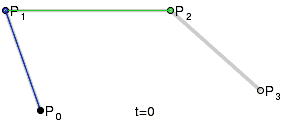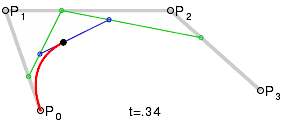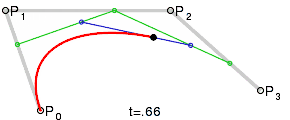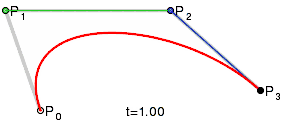
هر منحنی بزیه دو نقطه لنگر (به انگلیسی: anchor point) و دو نقطه کنترل (به انگلیسی: control point) دارد. نقطههای لنگر ابتدا و انتهای منحنی را مشخص میکنند و نقطههای کنترل انحنای مسیر را تعیین مینمایند. پارهخطی که یک نقطهٔ لنگر را به یک نقطهٔ کنترل وصل میکند به دستگیره (به انگلیسی: handle) معروف است.
اختراع
مبنای ریاضی منحنیهای بزیر - چند جمله ایهای Bernstein - در سال ۱۹۱۲ تأسیس شد، اما چند جمله ایها در گرافیک اعمال نشدند تا حدود ۵۰ سال بعد وقتی Paul de Casteljau ریاضیدان در ۱۹۵۹ الگوریتم De Casteljau، یک روش عددی پایدار برای ارزیابی منحنیها را ایجاد کرد، و اولین کسی بود که آنها را در طراحی اتومبیل سیتروئن به کمک رایانه اعمال کرد.[1] این چند جملهها در دهه ۱۹۶۰ توسط مهندس فرانسوی پیر بزیر، که از آنها برای طراحی بدنه اتومبیل در شرکت رنو استفاده میکرد، بهطور گسترده تبلیغ شد.
موارد خاص
منحنی بزیر توسط مجموعه ای از نقاط کنترل P 0 تا P n تعریف میشود، جایی که n ترتیب آن را مینامند (n = ۱ برای خطی، ۲ برای درجه دوم و غیره).) اولین و آخرین نقاط کنترل همیشه نقاط انتهایی منحنی هستند. با این حال، نقاط کنترل میانی (در صورت وجود) بهطور کلی روی منحنی قرار ندارند. مبالغ موجود در بخشهای زیر به عنوان ترکیبهای ترکیبی قابل درک است، ضرایب جمع شده به ۱.
منحنیهای خطی بزیه
با توجه به نقاط مجزا P 0 و P 1، یک منحنی خطی بزیر فقط یک خط مستقیم بین این دو نقطه است. منحنی توسط داده میشود
- و معادل درون یابی خطی است.
منحنیهای درجه یک بزیر
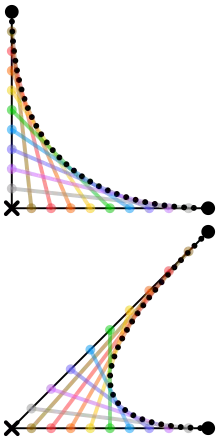
منحنی درجه دوم بزیر مسیری است که توسط تابع ردیابی میشود، با توجه به نقاط P 0، P 1 و P 2،
که به ترتیب میتواند به عنوان تقابل خطی نقاط متناظر در منحنیهای خطی بزیر از P 0 به P 1 و از P 1 به P 2 تفسیر شود. تنظیم مجدد بازده معادله قبلی:
این را میتوان به گونه ای نوشت که تقارن را با توجه به P 1 برجسته کند:
که بلافاصله مشتق منحنی بزیر را با توجه به t میدهد:
از آنجا میتوان نتیجه گرفت که مماسهای منحنی در P 0 و P 2 در P 1 قطع میشوند. وقتی t از ۰ به ۱ افزایش مییابد، منحنی حرکت از P 0 در جهت P 1، سپس خم میشود تا از جهت P 1، به P 2 برسد.
مشتق دوم منحنی بزیر با توجه به t است
منحنیهای مکعب بزیه
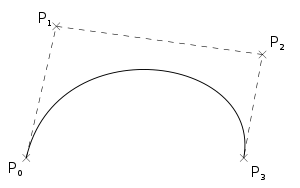
چهار نقطه P 0، P 1، P 2 و P 3 در صفحه یا در فضای بعد بالاتر، منحنی بزیه مکعبی را تعریف میکنند. منحنی از P 0 شروع میشود و به سمت P 1 میرود و و از جهت P 2،به P3 میرسد. معمولاً از P 1 یا P 2 عبور نخواهد کرد. این نقاط فقط برای ارائه اطلاعات جهت دار وجود دارد. فاصله بین P 1 و P 2 «تا چه حد» و «چگونه سریع» حرکت منحنی به سمت P 1 قبل از انحراف به سمت P 2 را تعیین میکند.
نوشتن BPi,Pj,Pk(t) برای منحنی درجه دوم بزیه که توسط نقاط P i، P j و P k تعریف شدهاست، منحنی بزیه مکعب را میتوان به عنوان ترکیبی از دو منحنی درجه دوم بزیر تعریف کرد:
فرم صریح منحنی به شرح زیر است:
برای بعضی از گزینههای P 1 و P 2 منحنی ممکن است خودش را قطع کند یا حاوی یک cusp باشد.
هر سری از ۴ نقطه مشخص را میتوان به یک منحنی بزیه مکعب تبدیل کرد که به ترتیب از هر ۴ نقطه عبور میکند. با توجه به نقطه شروع و پایان برخی از منحنیهای بزیر مکعب، و نقاط امتداد منحنی مربوط به t = ۱/۳ و t = ۲/۳، نقاط کنترل منحنی بزیر اصلی را میتوان بازیابی کرد.[2]
مشتق منحنی بزیر مکعب با توجه به t مقدار زیر است
مشتق دوم منحنی بزیر با توجه به t مقدار زیر است:
تعریف کلی
منحنیهای بزیر را میتوان برای هر درجه n تعریف کرد.
تعریف بازگشتی
یک تعریف بازگشتی برای منحنی بزیر از درجه n، آن را به عنوان یک ترکیب خطی نقطه به نقطه (درون یابی خطی) از یک جفت نقطه مربوطه در دو منحنی بزیر از درجه بیان میکند.
اجازه دهید منحنی بزیر را مشخص میکنیم که با انتخاب هر یک از نقاط P 0، P 1 ،. ، P n سپس برای شروع،
این بازگشت در انیمیشنهای زیر توضیح داده شدهاست.
تعریف صریح
فرمول را میتوان به صراحت به شرح زیر بیان کرد:
جایی که ضرایب دوجمله ای هستند.
به عنوان مثال، برای n = ۵:
واژهشناسی
برخی اصطلاحات با این منحنیهای پارامتریک مرتبط است. ما داریم:
چند جمله ایها:
به چند جمله ای پایه برنشتاین درجه n معروف هستند.
توجه داشته باشید که t 0 = ۱، (1 - t) 0 = ۱، و ضریب دوجمله ای ، ، است:
نقاط P i را برای منحنی بزیر نقاط کنترلی می نامند. چند ضلعی حاصل از اتصال نقاط بزیر با خطوط، شروع با P 0 و پایان دادن به P n، چند ضلعی بزیر (یا چند ضلعی کنترل) نامیده میشود. بدنه محدب چند ضلعی بزیر شامل منحنی بزیر است.
فرم چند جمله ای
گاهی اوقات مطلوب است که منحنی بزیر را به جای چندجمله چند جمله ای سادهتر برنشتاین به صورت چند جمله ای بیان کنید. استفاده از قضیه دوجمله ای در تعریف منحنی و به دنبال برخی از مقداری بازآرایی نتیجه میدهد:
که
این میتواند عملی باشد اگر میتواند قبل از بسیاری از ارزیابیها محاسبه شود ؛ با این وجود باید احتیاط کرد زیرا منحنیهای مرتبه بالا ممکن است از ثبات عددی برخوردار نباشند (در صورت بروز این الگوریتم دی Casteljau باید استفاده شود). توجه داشته باشید که محصول خالی ۱ است.
خواص
- منحنی از P 0 شروع میشود و در P n پایان مییابد. این ویژگی به اصطلاح نقطه درون یابی است.
- منحنی یک خط مستقیم اگر و تنها اگر تمام نقاط کنترلشونده خطی باشند.
- شروع و انتهای منحنی به ترتیب با قسمت اول و آخرین چند ضلعی بزیر مماس است.
- یک منحنی را میتوان در هر نقطه به دو زیر شاخه، یا به دلخواه بسیاری از زیرشاخهها تقسیم کرد که هر یک از آنها نیز منحنی بزیر است.
- برخی از منحنیهای ساده به نظر میرسند، مانند دایره، نمیتوان دقیقاً توسط منحنی بزیر یا بزیر بصورت قطعه ای توصیف کرد. اگرچه یک منحنی بزیر مکعب چهار قطعه میتواند یک دایره تقریبی را ببینید (به منحنی ترکیبی بزیر مراجعه کنید)، با حداکثر خطای شعاعی کمتر از یک قسمت در هزار، وقتی هر نقطه کنترل داخلی (یا نقطه آفلاین) فاصله باشد به صورت افقی یا عمودی از یک نقطه کنترل بیرونی روی یک دایره واحد. بهطور کلی، یک منحنی بزیه مکعب n-قطعه میتواند یک دایره را تقریبی بداند، زمانی که هر نقطه کنترل داخلی فاصله است از یک نقطه کنترل بیرونی روی یک دایره واحد، جایی که t 360 / n درجه است، و n > 2.
- هر منحنی درجه دوم بزیه نیز یک منحنی بزیر مکعب است، و بهطور کلی، هر منحنی بزیر درجه n نیز منحنی درجه m برای هر m > n است. بهطور جزئی، منحنی درجه n با نقاط کنترل P 0 ، . . ، P n معادل (با پارامتری سازی) منحنی درجه n + 1 با نقاط کنترل P ' 0، است. . . ، P ' n + 1، جایی که .
- منحنیهای بزیه دارای خاصیت کاهش تنوع هستند. معنای این از لحاظ شهودی این است که منحنی بزیر بیش از چند ضلعی نقاط کنترل خود را «موج دار شود» و ممکن است در واقع کمتر از آن «موج دار شود».[3]
- کنترل محلی در درجه n بزیر منحنی وجود ندارد. معنا ان این است که هر گونه تغییر به یک نقطه کنترل نیاز به تجدید محاسبه و در نتیجه جنبه از کل منحنی تأثیر میگذارد، "اگر چه بیشتر که یکی از نقطه کنترل کهتغییر شدهاست، تغییر در منحنی کوچکتر است ".[4]
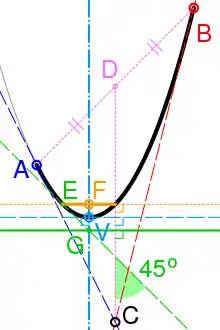 معادلات منحنی درجه یک Bézier و یک بخش سهموی
معادلات منحنی درجه یک Bézier و یک بخش سهموی - یک منحنی نظم بزیه بالاتر از دو ممکن است خودش را قطع کند یا برای برخی از گزینههای کنترل نقاط قعر باشد.
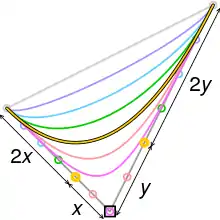
منحنی مرتبه دوم یک بخش سهمی است
منحنی درجه دوم بزیه نیز بخشی از یک سهمی است. از آنجا که سهمی یک بخش مخروطی است، برخی منابع از بزیههای درجه دوم به عنوان «قوسهای مخروطی» یاد میکنند.[5] با اشاره به شکل سمت راست، ویژگیهای مهم سهمی را میتوان به شرح زیر بدست آورد:[6]
- مماسهای سهمی در نقاط انتهایی منحنی (A و B) در نقطه کنترل آن (C) تلاقی میکنند.
- اگر D نقطه میانی AB باشد، مماس منحنی عمود بر CD (خط فیروزه ای خط دار) راس آن را تعریف میکند (V). محور تقارن آن (خط فیروزه ای) از V عبور میکند و عمود بر مماس است.
- E یا نقطه ای از منحنی با مماس در ۴۵ درجه به CD (سبز تیره) است. اگر G محل تلاقی این مماس و محور باشد، خط عبوری از G و عمود بر CD، دایرکتریکس (سبز جامد) است.
- کانون (F) در تقاطع محور و خطی است که از E عبور میکند و عمود بر CD است (زرد نقطه دار). راست روده (Latus rectum) قطعه خط درون منحنی (زرد جامد) است.
مشتق
مشتق منحنی سفارش n است
ساخت منحنیهای بزیه
منحنیهای خطی
t در تابع را برای یک منحنی خطی بزیه میتوان تصور کرد که فاصله B (t) از P 0 به P 1 چیست. به عنوان مثال، وقتی t = ۰٫۲۵، B (t) یک چهارم راه از نقطه P 0 به P 1 است. از آنجا که t از ۰ تا ۱ متغیر است، B (t) یک خط مستقیم از P 0 به P 1 را توصیف میکند.
منحنی درجه دوم
برای منحنیهای درجه دوم بزی میتوان نقاط میانی Q 0 و Q 1 را طوری ساخت که t از ۰ تا ۱ متغیر باشد:
- نقطه از P 0 تا P 1 متغیر است و یک منحنی خطی بزیه را توصیف میکند.
- نقطه از P 1 تا P 2 متفاوت است و منحنی خطی بزیه را توصیف میکند.
- نقطه B (t) بین تا به صورت خطی درون یابی میشود و منحنی درجه دوم بزیر را توصیف میکند.
منحنیهای مرتبه بالاتر
برای منحنیهای مرتبه بالاتر شخص به نقاط میانی بیشتری احتیاج دارد. برای منحنیهای مکعبی میتوان نقاط میانی Q 0، Q 1 و Q 2 را که منحنیهای خطی بزیه را توصیف میکند و نقاط R 0 & R 1 را که منحنیهای درجه دوم بزیه را توصیف میکنند، ساخت:
برای منحنیهای مرتبه چهارم میتوان نقاط میانی Q 0، Q 1، Q 2 و Q 3 را ساخت که منحنیهای خطی بزیه، نقاط R 0، R 1 و R 2 را توصیف میکند که منحنیهای درجه دوم بزیه و نقاط S 0 & S 1 را توصیف میکند. منحنیهای بزیه مکعبی را توصیف کنید:
برای منحنیهای مرتبه پنجم، میتوان نقاط میانی مشابهی را ساخت.
این نمایشها متکی بر فرایند مورد استفاده در الگوریتم De Casteljau برای محاسبه منحنیهای بزیر است.[7]
جبران کردن (معروف به نوازش) منحنیهای بزیه
منحنی در یک جابجایی ثابت از یک منحنی بزیه داده نمیشود، که در ریاضیات منحنی افست یا موازی نامیده میشود ("موازی" با منحنی اصلی قرار دارد، مانند جابجایی بین ریلها در یک مسیر راهآهن)، دقیقاً توسط یک منحنی بزیر تشکیل نمیشود (به جز در برخی موارد پیش پا افتاده). بهطور کلی، منحنی انحراف دو طرفه بزیر مکعب یک منحنی جبری مرتبه ۱۰ است[8] و بهطور کلی برای یک بزیه درجه n منحنی انحراف دو طرفه یک منحنی جبری درجه ۴ ، است.[9] با این حال، روشهای ابتکاری وجود دارد که معمولاً تقریب مناسبی را برای اهداف عملی ارائه میدهند.[10]
در زمینه گرافیک برداری، به رنگ آمیزی دو منحنی افست با تقارن متقارن نوازش گفته میشود (منحنی بزیر یا بهطور کلی مسیری از چندین بخش بزیر).[11] تبدیل از منحنیهای افست به خطوط پر شده بزیر از اهمیت عملی در تبدیل فونتهای تعریف شده در Metafont است که اجازه میدهد تا منحنیهای بزیر را به فونتهای نوع 1 PostScript که بهطور گسترده استفاده میشود، تبدیل کنید. پر کردن یک کانتور مشخص شده توسط منحنیهای بزیر (غیر خود تلاقی).[12]
ارتفاع درجه
منحنی بزیر از درجه n میتواند به منحنی بزیر از درجه n+1 با همان شکل تبدیل شود. این در صورتی مفید است که نرمافزار منحنیهای بزیر را فقط در درجه خاص پشتیبانی کند. به عنوان مثال، سیستمهایی که فقط میتوانند با منحنیهای مکعبی مکعبی کار کنند، میتوانند با استفاده از نمایش مکعب معادل آنها، بهطور ضمنی با منحنیهای درجه دوم کار کنند.
برای انجام ارتفاع درجه، از برابری استفاده میکنیم . هر مولفه ضرب در (1 − t) میشود و t، بنابراین یک درجه بدون تغییر مقدار افزایش مییابد. در اینجا مثالی برای افزایش درجه از ۲ به ۳:
برای n دلخواه از برابری استفاده میکنیم
از این رو:
معرفی دلخواه و .
بنابراین، نقاط کنترل جدید[13]
تکرار درجه ارتفاع
مفهوم ارتفاع درجه را میتوان بر روی چند ضلعی کنترل R تکرار کرد تا توالی چند ضلعیهای کنترل R , R 1، R 2 و غیره بدست آید. بعد از افزایش درجه r، چند ضلعی R r دارای رئوس P 0، r، P 1، r، P 2، r، است. . ، P n + r، r داده شده توسط[14]
همچنین میتوان نشان داد که برای منحنی بزیه زیرین B ,
منحنیهای بزیه منطقی
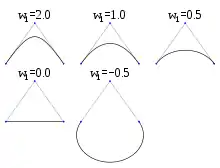
منحنی بیزیر منطقی وزنی قابل تنظیم برای ایجاد تقریب نزدیک به اشکال دلخواه اضافه میکند. عدد یک منحنی وزنی شکل بزیر به شکل برنشتاین است و مخرج یک مجموع وزنی از چند جملههای برنشتاین است. از منحنیهای منطقی بزیر، در میان سایر کاربردها، میتوان برای نمایش دقیق بخشهای مخروطی، از جمله قوسهای دایره ای استفاده کرد.[15]
با توجه به نقاط کنترل P i، منحنی بزیر منطقی را میتوان با شرح زیر توصیف کرد:
یا به سادگی
این عبارت را میتوان با استفاده از سیستمهای عددی علاوه بر واقعی برای اوزان، گسترش داد. در صفحه پیچیده، نقاط {۱}، {-۱} و {۱} با وزن { }، {۱} و { } یک دایره کامل با شعاع یک ایجاد کنید. برای منحنیهای دارای نقطه و وزن روی یک دایره، وزنها را میتوان بدون تغییر شکل منحنی مقیاس بندی کرد.[16] مقیاس گذاری وزن مرکزی منحنی فوق توسط ۱٫۳۵۵۰۸، پارامتر سازی یکنواخت تری را به دست میدهد.
برنامههای کاربردی
گرافیک کامپیوتری

منحنیهای بزیر بهطور گستردهای در گرافیک کامپیوتر برای مدلسازی منحنیهای صاف استفاده میشود. از آنجا که منحنی کاملاً در پوسته محدب نقاط کنترل آن قرار دارد، میتوان نقاط را به صورت گرافیکی نمایش داد و از آنها برای دستکاری بصری بصورت منحنی استفاده کرد. با اعمال تغییر شکل مربوط به نقاط کنترل منحنی، میتوان تبدیلات آفین مانند ترجمه و چرخش را روی منحنی اعمال کرد.
منحنیهای درجه دوم و مکعب بزیر بیشترین شیوع را دارند. منحنیهای درجه بالاتر برای ارزیابی از نظر محاسباتی گران ترند. در صورت نیاز به اشکال پیچیدهتر، منحنیهای کمنظیر بزیر به هم وصل میشوند و یک منحنی بزیر مرکب تولید میکنند. از منحنی ترکیبی بزیر معمولاً به عنوان «مسیر» در زبانهای گرافیکی برداری (مانند PostScript)، استانداردهای گرافیکی برداری (مانند SVG) و برنامههای گرافیکی برداری (مانند Artline، Timeworks Publisher، Adobe Illustrator، CorelDraw، Inkscape و Allegro) یاد میشود. . به منظور پیوستن منحنیهای بزیر به یک منحنی ترکیبی بزیر و بدون انحراف، خاصیتی به نام G1 مداوم، کافی است که نقطه کنترل

ی را که در آن دو منحنی تشکیل دهنده بزیر به هم میرسند، مجبور کنیم در روی خط مشخص شده توسط دو نقطه کنترل در دو طرف قرار بگیریم.
سادهترین روش برای تبدیل اسکن (تصادفی سازی) منحنی بزیر ارزیابی آن در بسیاری از نقاط با فاصله نزدیک و اسکن تبدیل توالی تقریبی بخشهای خط است. با این حال، این تضمین نمیکند که خروجی تصادفی شده به اندازه کافی صاف به نظر میرسد، زیرا ممکن است نقاط از یکدیگر بسیار دور باشند. برعکس ممکن است در مناطقی که منحنی نزدیک به خطی است، نقاط زیادی ایجاد کند. یک روش تطبیقی معمول، تقسیم بازگشتی است که در آن نقاط کنترل یک منحنی بررسی میشود تا ببیند که آیا منحنی به یک خط مستقیم نزدیک به یک تحمل کوچک است. در غیر این صورت، منحنی از نظر پارامتری به دو بخش و تقسیم میشود و روش مشابه بهطور بازگشتی برای هر نیمه اعمال میشود. روشهای متمایزسازی به جلو نیز وجود دارد، اما باید برای تجزیه و تحلیل انتشار خطا بسیار دقت شود.[18]
روشهای تحلیلی که یک بزیر با هر خط اسکن قطع میشود شامل یافتن ریشههای چند جمله ای مکعبی (برای بزیههای مکعبی) و مقابله با چندین ریشه است، بنابراین آنها در عمل اغلب استفاده نمیشوند.[19]
الگوریتم rasterisation مورد استفاده در Metafont مبتنی بر تشخیص منحنی است، به طوری که با دنباله ای از "حرکتهای rook " که کاملاً عمودی یا کاملاً افقی هستند، در امتداد مرزهای پیکسل تقریب مییابد. بدین منظور، هواپیما ابتدا به هشت بخش ۴۵ درجه تقسیم میشود (توسط محورهای مختصات و دو خط )، سپس منحنی به بخشهای کوچکتر تجزیه میشود، به طوری که جهت یک بخش منحنی در یک بخش باقی میماند. از آنجا که سرعت منحنی یک چند جمله ای درجه دو است، پیدا کردن مقادیری که موازی یکی از این خطوط باشد را میتوان با حل معادلات درجه دوم انجام داد. در هر بخش، حرکت افقی یا عمودی غالب است و تعداد کل مراحل در هر جهت را میتوان از مختصات نقطه انتهایی خواند. برای مثال حرکت افقی بخش ۰–۴۵ درجه به سمت راست غالب است، بنابراین فقط باید تصمیم بگیرید که بین کدام پلهها به سمت راست منحنی باید یک پله بالا برود.[20]
انیمیشن
در برنامههای انیمیشن سازی، مانند Adobe Flash و Synfig، از منحنیهای بزیه برای طرح کلی، به عنوان مثال حرکت، استفاده میشود. کاربران مسیر مورد نظر را در منحنیهای بزیه ترسیم میکنند، و برنامه قابهای لازم را برای حرکت جسم در طول مسیر ایجاد میکند.[21][22]
در انیمیشن سه بعدی، منحنیهای بزیه اغلب برای تعریف مسیرهای سه بعدی و همچنین منحنیهای دو بعدی برای درهم آمیختن فریم کلیدی استفاده میشوند.[23] منحنیهای بزیر اکنون بطور مداوم برای کنترل کاهش انیمیشن در CSS، JavaScript و JavaFx استفاده میشود.
قلمها
قلمهای TrueType از منحنیهای بزیر مرکب متشکل از منحنیهای درجه دوم بزیر استفاده میکنند. زبانهای دیگر و ابزارهای تصویربرداری (مانند PostScript، Asymptote، Metafont و SVG) از بزیر مرکب متشکل از منحنیهای بزیر مکعب برای ترسیم اشکال منحنی استفاده میکنند. بسته به طعم قلم، قلمهای OpenType میتوانند از هر دو نوع استفاده کنند.[24]
رندر داخلی تمام منحنیهای بزیر در رندرهای فونت یا گرافیک برداری، آنها را به صورت بازگشتی تقسیم میکند تا جایی که منحنی به اندازه کافی مسطح باشد تا به صورت مجموعه ای از بخشهای خطی یا دایره ای ترسیم شود. الگوریتم تقسیم دقیق به اجرا وابسته است، فقط معیارهای مسطح بودن باید رعایت شود تا به دقت لازم برسد و از تغییر موضع منحنی غیر یکنواخت جلوگیری کند. ویژگی «منحنی روان» نمودارها در Microsoft Excel نیز از این الگوریتم استفاده میکند.[25]
از آنجا که قوس دایرهها و بیضیها را نمیتوان دقیقاً توسط منحنیهای بزیر نشان داد، ابتدا با منحنیهای بزیر تقریب میشوند که به نوبه خود با قوسهای دایرهها تقریب میشوند. این ناکارآمد است زیرا تقریبهای منحنی بزیر با استفاده از کمانهای دایره یا بیضی نیز وجود دارد، که میتواند با دقت دلخواه به صورت تدریجی ارائه شود. رویکرد دیگری که توسط آداپتورهای گرافیکی سختافزاری مدرن با هندسه شتابدهنده استفاده میشود، میتواند دقیقاً تمام منحنیهای بزیر و مخروطی (یا سطوح) را به NURBS تبدیل کند، که میتواند بدون تقسیم منحنی به صورت بازگشتی به صورت افزایشی ارائه شود تا به شرایط مسطح لازم برسد. این روش همچنین اجازه میدهد تا تعریف منحنی را تحت همه تبدیلها و پیشبینیهای 2D و 3D خطی یا پرسپکتیو حفظ کنیم.
موتورهای قلم، مانند FreeType، منحنیهای قلم (و خطوط) را با استفاده از فرایندی که به عنوان rasterization قلم شناخته میشود، روی یک سطح پیکسلی ترسیم میکنند.[26]
جستارهای وابسته
منابع
- Empty citation (help)
- John Burkardt. "Forcing Bezier Interpolation". Archived from the original on 2013-12-25.
- Empty citation (help)
- Empty citation (help)
- "FreeType Glyph Conventions / VI. FreeType outlines". The Free Type Project. 13 February 2018."FreeType Glyph Conventions – Version 2.1 / VI. FreeType outlines". 6 March 2011. Archived from the original on 2011-09-29.
- Empty citation (help)
- Shene, C. K. "Finding a Point on a Bézier Curve: De Casteljau's Algorithm". Retrieved 6 September 2012.
- Mark Kilgard (April 10, 2012). "CS 354 Vector Graphics & Path Rendering". p. 28.
- Rida T. Farouki. "Introduction to Pythagorean-hodograph curves" (PDF)., particularly p. 16 "taxonomy of offset curves".
- For example: or. For a survey see.
- Mark Kilgard (April 10, 2012). "CS 354 Vector Graphics & Path Rendering". p. 28.
- Richard J. Kinch (1995). "MetaFog: Converting Metafont shapes to contours" (PDF). TUGboat. 16 (3–Proceedings of the 1995 Annual Meeting).
- Empty citation (help)
- Empty citation (help)
- Neil Dodgson (2000-09-25). "Some Mathematical Elements of Graphics: Rational B-splines". Retrieved 2009-02-23.
- J. Sánchez-Reyes (November 2009). "Complex rational Bézier curves". Computer Aided Geometric Design. 26 (8): 865–876. doi:10.1016/j.cagd.2009.06.003.
- Alexander Reshetov and David Luebke, Phantom Ray-Hair Intersector. In Proceedings of the ACM on Computer Graphics and Interactive Techniques (August 1, 2018).
- Xuexiang Li; Junxiao Xue. "Complex Quadratic Bézier Curve on Unit Circle". Zhengzhou, China: School of Software, Zhengzhou University.
- Xuexiang Li; Junxiao Xue. "Complex Quadratic Bézier Curve on Unit Circle". Zhengzhou, China: School of Software, Zhengzhou University.
- Parts 19–22 of Empty citation (help)
- "Using motion paths in animations". Adobe. Retrieved 2019-04-11.
- "Following a Spline". Synfig Wiki. Retrieved 2019-04-11.
- Dodgson, Neil A. (1999). "Advanced Graphics Lecture Notes" (PDF). cl.cam.ac.uk. University of Cambridge Computer Laboratory.
- "The difference between CFF and TTF". Know How. Linotype. Archived from the original on 2017-07-03. Retrieved 3 July 2018.
The OpenType format was formulated in 1996. By 2003, it began to replace two competing formats: the Type1 fonts, developed by Adobe and based on [P]ost[S]cript, and the TrueType fonts, specified by Microsoft and Apple. (...) TTF stands for TrueTypeFont and indicates that the font data is the same as in the TrueType fonts. CFF stands for the Type1 font format. Strictly speaking, it refers to the Compact Font Format, which is used in the compression processes for the Type2 fonts. (...) the cubic Bézier format of the Type1 fonts is more space-saving compared to the quadratic format of the TrueType fonts. Some kilobytes can be saved in large, elaborate fonts, which may represent an advantage on the Web. On the other hand, the more detailed hinting information of the TrueType fonts allows very extensive optimization for screen use.
- "smooth_curve_bezier_example_file.xls". Rotating Machinery Analysis, Inc. Archived from the original on 2011-07-18. Retrieved 2011-02-05.
- "FreeType Glyph Conventions / VI. FreeType outlines". The Free Type Project. 13 February 2018."FreeType Glyph Conventions – Version 2.1 / VI. FreeType outlines". 6 March 2011. Archived from the original on 2011-09-29.
- Empty citation (help)
- مشارکتکنندگان ویکیپدیا. «Bézier curve». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲۴ ژانویه ۲۰۱۸.
