تجزیه مقدارهای منفرد
روش تجزیه مقادیر منفرد یا SVD تاریخچه طولانی و البته جالبی دارد. این روش، در علوم اجتماعی و با تست هوش شروع شد. در گذشته، پژوهشگران آزمونهایی را برای اندازهگیری جنبههای مختلف هوش مانند هوش فضایی و هوش کلامی ارائه کردند که همبستگی زیادی با هم داشتند. آنها بر این باور بودند که یک معیار عمومی مشترک برای هوش وجود دارد و آن را برای هوش کلی، g نامیدند که امروزه بیشتر به عنوان آی کیو (IQ) شناخته میشود؛ بنابراین، پژوهشگران تصمیم گرفتند عوامل مختلف هوش را تجزیه و مهمترین آنها را انتخاب کنند. در سادهترین حالت، تجزیه مقادیر منفرد به نوعی همین تجزیه و انتخاب مهمترین عوامل یک ماتریس را انجام میدهد.

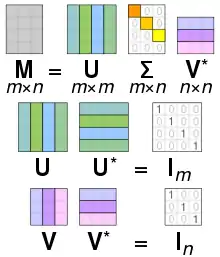
تجزیه مقادیر منفرد (به انگلیسی: Singular Value Decomposition) یا SVD با نامهای مختلفی شناخته میشود. این روش، ابتدا به عنوان «تجزیه عامل» (به انگلیسی: Factor Analysis) نامیده میشد. تحلیل مؤلفههای اصلی (به انگلیسی: Principal Component) یا PC و تجزیه توابع متعامد تجربی (به انگلیسی: Empirical Orthogonal Function) یا EOF نیز از دیگر اصطلاحات نزدیک به این روش است. همه این نامها از نظر مفهوم ریاضی معادل هستند، هرچند در فرایند محاسبه آنها تفاوتهای زیادی وجود دارد
امروزه، تجزیه مقادیر منفرد در بسیاری از شاخههای علوم و نجوم کاربرد دارد. این روش، در یادگیری ماشین و آمار توصیفی و مدلسازی آماری نیز بسیار مورد استفاده قرار میگیرد.
به عنوان یک تجزیه و فاکتورگیری ماتریسی، تجزیهٔ مقدارهای منفرد یا تجزیهٔ مقدارهای تکین (به انگلیسی: Singular value decomposition) قدمی اساسی در بسیاری از محاسبات علمی و مهندسی بهحساب میآید.
در حل بسیاری از مسائل، مشکلاتی وجود دارد که نیازمند روشهایی برای حل آنها میباشیم. تجزیهٔ مقدار تکین یکی از این روشها میباشد که:
- در فضای پر داده و دارای خطاهایی نظیر خطای گردکردن قابل استفاده میباشد.
- در حل معادلات و ماتریسها نزدیک به تکینگی و در حالت تکینه قابل استفاده است.
- میتواند مشکل حل را بهطور دقیق باز کند.
- گاهی میتواند علاوه بر شرح مشکل مسئله آن را نیز حل کند.
و در نهایت جواب عددی مناسبی از فضای حل را میتواند ارائه کند. اما باید توجه داشت که این روش به یقین جواب اصلی معادلات را نمیدهد.
به عبارتی دیگر، در جبر خطی، تجزیه مقدار تکین فاکتورگیری از یک ماتریس موهومی یا حقیقی میباشد که تجزیه مقادیر ویزه یک ماتریس نرمال را به هر ماتریس با M سطر و N ستون به وسیله توسعه تجزیه قطبی تعمیم میدهد. بهطور خاص، این روش تجزیه ماتریس را به فرم تبدیل میکند که در آن U یک ماتریس واحد با M سطر و ستون است،یک ماتریس مستطیلی با درایههای غیر منفی بر روی قطر اصلی و ماتریس V یک ماتریس واحد با N سطر و ستون میباشد.
تجزیه مقادیر تکین یکتا نیست. همیشه ممکن است که ترکیبهایی را انتخاب کرد که مقادیر تکین بهصورت کاهنده مرتب شدهباشند. در چنین حالتی بهصورت خاص از ماتریس M حاصل میگردد.
گاهی نیز از اصطلاح تجزیه فشرده مقادیر تکین نیز یاد میشود که در آن ماتریس مقادیر ویژه یک ماتریس مربعی قطری میباشد که مرتبه ماتریس است و فقط شامل مقادیر ویژه غیر صفر میباشد. در این حالت، ماتریس U یک ماتریس و ماتریس V یک ماتریس هستند بهصورتی که .
امروزه، تجزیه مقادیر منفرد در بسیاری از شاخههای علوم و نجوم کاربرد دارد. این روش، در یادگیری ماشین و آمار توصیفی و مدلسازی آماری نیز بسیار مورد استفاده قرار میگیرد.
کاربردهای ریاضی SVD شامل محاسبه شبه معکوس، تقریب ماتریس و تعیین رتبه، دامنه و فضای تهی یک ماتریس است. SVD همچنین در کلیه زمینههای علمی و مهندسی بسیار مفید است مانند پردازش سیگنال، حداقل مربعات مناسب دادهها و کنترل فرایند.
البته که محاسبهٔ SVD برای یک ماتریسْ دارای پیچیدگیِ زمانی خوبی نیست ولی به هر حال این روش یکی از روشهای شناخته شده در کاهشِ ویژگیها در دادهکاوی میباشد و کاربردهای دیگرِ آن نیز در ادامه مورد بحث قرار خواهد گرفت. در زبانهای برنامهنویسی مانند Python و R میتوانید کتابخانههای مختلفی را پیدا کنید که این عملیات را به سادگی برای شما انجام میدهند.
تاریخچه
تجزیه مقادیر مفرد در ابتدا توسط هندسههای دیفرانسیل توسعه یافته بود، که مایل بودند با تبدیلهای متعامد مستقل، از دو فضایی که بر روی آن عمل میکنند، مشخص کنند که آیا یک شکل دوقلو واقعی میتواند برابر شکل دیگری باشد یا خیر. Eugenio Beltrami و Camille Jordan بهطور مستقل، در سالهای ۱۸۷۳ و ۱۸۷۴ بهطور مستقل کشف کردند که مقادیر منفرد دو شکل، که به عنوان ماتریس نشان داده میشود، یک مجموعه کامل را از ثوابت برای اشکال دوقلو را تحت تعویضهای متعامد تشکیل میدهد. همچنین جیمز جوزف سیلوستر در سال ۱۸۸۹ بهطور مستقل از بلترامی و اردن به تجزیه مقادیر منفرد برای ماتریسهای مربع رسید. سیلوستر مقادیر مفرد را ضربهای متعارف ماتریس A نامید. چهارمین ریاضیدان برای کشف تجزیه ارزش مفرد بهطور مستقل، Autonne در سال ۱۹۱۵ است که از طریق تجزیه قطبی به آن دست یافت. به نظر میرسد اولین اثبات تجزیه ارزش مفرد برای ماتریسهای مستطیل و پیچیده توسط کارل اکارت و گیل جی جوان در سال ۱۹۳۶ است که آن را به عنوان تعمیم تغییر محور اصلی ماتریسهای هرمیتی میدیدند.
در سال ۱۹۰۷، ارهارد اشمیت یک آنالوگ از مقادیر مفرد را برای اپراتورهای انتگرال (تحت برخی فرضیات فنی ضعیف) تعریف کرد. به نظر میرسد وی از کار موازی روی مقادیر مفرد ماتریسهای محدود آگاه نبود. این نظریه پیشتر توسط ilemile Picard در سال ۱۹۱۰ ساخته شد، که اولین کسی است که اعداد را با مقادیر مفرد sigma مینامد.
روشهای عملی نیز برای محاسبه SVD به Kogbetliantz در سال ۱۹۵۴، ۱۹۵۵ و Hestenes در ۱۹۵۸ بازمیگردد. روشهایی که شبیه به روش eigenvalue Jacobi عمل میکرد. با این حال، این روشها با روشی که Gene Golub و ویلیام کاهان که در سال ۱۹۶۵ منتشر کردند، جایگزین شدند. درنهایت در سال ۱۹۷۰، Golub و Christian Reinsch نوعی از الگوریتم Golub / Kahan را منتشر کردند که امروزه هنوز هم مورد استفاده قرار میگیرد.
تعبیر شهودی تجزیه مقدار منفرد
دوران، پیمایش مختصات
در مورد خاص، زمانی که M یک ماتریس مربع حقیقی است، ماتریس و را میتوان ماتریسهای یکه حقیقی نیز انتخاب کرد. در این حالت، «یکه بودن» همان «متعامد» است. سپس با تفسیر هر یک از ماتریسهای A به عنوان تبدیل خطی محور فضای ، ماتریسهای و دوران فضا را نشان میدهند، در حالی که نمایانگر مقیاس هر مختصات xi توسط عامل σi است؛ بنابراین تجزیه مقدار منفرد هرگونه تغییر خطی برگشتپذیر را به ترکیبی از سه دگرگونی هندسی تجزیه میکند: چرخش یا بازتاب ()، و به دنبال آن یک مقیاس مختصات () و به دنبال آن چرخش یا بازتاب دیگر ().
بهطور خاص، اگر M یک دترمینان مثبت داشته باشد، میتوان و را طوری انتخاب کرد که هر دو بازتاب یا دوران باشند. اگر دترمینان منفی باشد، دقیقاً یکی از آنها باید بازتاب کننده فضا باشد. اگر دترمینان صفر باشد، میتوان هر کدام را بهطور مستقل انتخاب کرد.
اگر ماتریس M حقیقی باشد اما مربعی نباشند، یعنی با ، میتوان آن را به عنوان یک تبدیل خطی از به تفسیر کرد. سپس و میتوانند به ترتیب چرخش و انتخاب شوند؛ و ، علاوه بر مقیاس کردن مختصات ، همچنین بردار را با صفرها گسترش میدهد، یا دنباله مختصات را حذف میکند، تا نهایت فضای را به تبدیل کند.
مقادیر ویژه به عنوان شبه محور بیضوی
همانطور که در شکل نشان داده شدهاست، مقادیر تکین میتوانند به عنوان اندازه نیم محور یک بیضی در 2D تعبیر شوند. این مفهوم را میتوان به فضای بعدی اقلیدسی تعمیم داد، با مقادیر تکین هر ماتریس مربع به عنوان اندازه نیم محور یک بیضی n بعدی مشاهده میشود. بهطور مشابه، مقادیر تکین هر ماتریس را میتوان به عنوان اندازه نیم محور یک بیضی n بعدی در فضای m بعدی مشاهده کرد، به عنوان مثال به عنوان بیضی در یک صفحه (کج) 2D در یک فضای 3D. مقادیر مفرد اندازه نیم محور را تعیین میکنند، در حالی که بردارهای تکین جهت را تعیین میکنند.
مفهوم هندسی
از آنجا که U و V یکه هستند، میدانیم که ستونهای U از U1، … ، Um یک پایه متعامد و ستونهای V از V1، … ، Vn یک پایه متعامد از (با توجه به ضرب استاندارد اسکالر در این فضاها).
تبدیل خطی:
توضیحی به خصوص ساده با توجه به اساس تعامد دارد: ما داریم
که در آن سیگما مقدار قطری ماتریس است و برای مقادیر کمتر از کمینه مقدار سطر وستون .
از این رو مفهوم هندسی قضیه تجزیه مقدار تکین به شرح زیر خلاصه میشود:
برای هر نگاشت خطی میتوان پایههای متعامد متعارف و را پیدا کرد به گونه ای که T به i امین بردار پایه از را به یک ضرب غیر منفی از بردار پایه I از تبدیل کند، و باقی بردارهای پایه را صفر کند. با توجه به این اساس، نگاشت T از این رو توسط یک ماتریس قطری با ورودیهای قطری حقیقی غیر منفی نشان داده میشود.
برای درک بهتر تجزیه مقدار تکین و فاکتورگیری آن، حداقل در هنگام استفاده از فضای برداری، یک کره با شعاع یک را در نظر بگیرید. نگاشت خطی T این کره را بر روی فضای بیضوی تصویر میکند. مقادیر تکین غیر صفر به سادگی طول محورهای نیمه بیضه این فضای بیضوی هستند. به خصوص وقتی که n = m باشد، و تمام مقادیر مفرد مشخص و غیر صفر باشند، تجزیه مقدار تکین نگاشت خطی T به راحتی میتواند به عنوان سه حرکت متوالی مورد تجزیه و تحلیل قرار گیرد: بیضی (s)T و بهطور خاص محورهای آن را در نظر بگیرید. سپس جهتهای منتقل شده توسط T را بر روی این محورها در نظر بگیرید. این جهتها بهطور متقابل متعامد هستند. عمل کرد یک ماتریس این جهتها را به فضای انتقال میدهد. حرکت دوم، یک دگرگونی قطری در راستای محور مختصات وارد میسازد و با استفاده از طول نیمه محورهای(s)T به عنوان ضریب کشیدگی، در هر راستا کشیده یا کوچک میشود. ترکیب ماتریس قطری در سپس کره واحد را در فضای بیضوی به(S)Tمیبرد. به جهت تعریف آخرین حرکت که حرکت ماتریس U است، فضایی را به فضای بیضوی اضافه کنید که آن را بر روی (S)Tمیبرد. به راحتی میتوان بررسی کرد که، با مطابقت دارد.
ماتریسهای متعامد U و V
از آنجا که و یکه هستند، ستونهای هریک از آنها مجموعه ای از بردارهای متعامد را تشکیل میدهند، که میتوانند به عنوان بردارهای پایه در نظر گرفته شوند. ماتریس M بردار پایه Vi را به بردار واحد کشیده نگاشت میکند. بهصورت خلاصه و متعامد هستند و حاصل آنها ماتریس واحد خواهد بود.
مقادیر منفرده کاسته
در عمل تجزیه کامل مقادیر تکین، که نیازمند تجزیه کامل فضای تهی نیز هست. مورد نیاز نیست. در عوض گاهی بهتر است که از حالت کاهش یافتهٔ آن استفاده گردد.
تجزیه مقدار تکین سبک
فقط بردارهای ستون n از مربوط به بردارهای ردیف محاسبه میشوند. بردارهای ستون باقیمانده U محاسبه نمیشوند. اگر سریعتر از تجزیهٔ کامل مقادیر تکین محاسبه میگردد. ماتریس به این ترتیب یک ماتریس و یک ماتریس قطری و در نهایت یک ماتریس خواهد بود.
مرحله اول در محاسبه SVD سبک معمولاً تجزیه QR از M است، که میتواند محاسبه ای بهطور قابل توجهی سریعتر انجام دهداگر باشد.
تجزیه مقدار تکین فشرده
فقط بردارهای ستون r از بردارهای ردیف و r از مربوط به مقادیر مفرد غیر صفر محاسبه میشوند. بردارهای باقیمانده و محاسبه نمیشوند. اگر سریعتر و مقرون به صرفه تر باشد از SVD سبک خواهد بود. ماتریس به این ترتیب یک ماتریس و یک ماتریس قطری و در نهایت یک ماتریس خواهد بود.
تجزیه مقدار تکین کوتاه شده
فقط بردارهای ستون t از بردارهای ردیف و t از مربوط به مقادیر مفرد غیر صفر محاسبه میشوند. بردارهای باقیمانده و محاسبه نمیشوند. اگر سریعتر و مقرون به صرفه تر باشد از SVD فشرده خواهد بود. ماتریس به این ترتیب یک ماتریس و یک ماتریس قطری و در نهایت یک ماتریس خواهد بود.
مقادیری که در سیگما وجود دارد در واقع همان مقادیرِ منحصر به فردی (Singular) است که میتواند در عملیاتِ کاهشِ ویژگی به ما کمک کند. ممکن است برای کسانی که با دادهکاوی و عملیاتِ کاهشِ ویژگی کار نکرده باشند کمی مبهم به نظر برسد ولی در ادامه، آرام آرام این مباحث در ذهن جای خود را پیدا میکنند. در ادامه نیز کاهش داده به صورت کلی توضیح داده شدهاست.
محاسبهٔ مقادیر منفرد
تجزیه مقدار تکین را میتوان به صورت زیر مشاهد کرد:
- بردارهای تکین چپ ماتریس M مجموعهای از بردارهای تکین هستند.
- بردارهای نکین راست ماتریسM مجموعهای از بردارهای تکین هستند.
- مقادیر ویژه غیر منفی ماتریس M جذر ریشه مقادیر تکین هر دو ماتریس و هستند.
رویکرد عددی
یک ماتریس M معمولاً با بهصورت دو مرحله ای محاسبه میشود. در مرحله اول، ماتریس به یک ماتریس دو قطری کاهش مییابد. مرحله دوم SVD محاسبه ماتریس دو قطری است. این مرحله فقط با یک روش تکراری (مانند الگوریتمهای و مقادیر ویژه) قابل انجام است. با این حال، در عمل محاسبه SVD تا دقت خاصی مانند دستگاه اپسیلون کافی است. اگر این دقت ثابت در نظر گرفته شود، n مرتبه تکرار نیاز دارد که هر کدام فلوتینگ پوینت از مرتبه n دارند.
اولین قدم را میتوان با استفاده از بازتابهای Householder با هزینه 4mn2 - 4n3 / ۳ فلاپ انجام داد، با این فرض که فقط مقادیر تکین مورد نیاز هستند و نه بردارهای تکین. اگر m بسیار بزرگتر از n باشد، کاهش ماتریس M به به یک ماتریس سه قطری توسط روش QR و پس از آن تبدیل به یک ماتریس دو قطری با استفاده از روش Householder یک مزیت با هزینه کم محاسباتی خواهد بود.
مرحله دوم را میتوان با یک نوع از الگوریتم QR برای محاسبه مقادیر ویژه انجام داد که برای اولین بار توسط Golub & Kahan (1965) بیان شدهاست. سابروتینLAPACK با نام DGESVD این روش تکرار را با کمی اصلاح برای مقدار کم مقادیر تکین پوشش میدهد.
همین الگوریتم در کتابخانه علمی GNU (GSL) پیادهسازی شدهاست. GSL همچنین یک روش جایگزین ارائه میدهد که از یک طرفه سازی جاکوبی یک طرفه در مرحله ۲ استفاده میکند (GSL Team 2007). این روش ماتریس SVD دو قطری را با حل توالی از مسئلههای ۲ × 2 SVD، شبیه به نحوه حل الگوریتم eigenvalue Jacobi، از روشهای ۲ × ۲ مقادیر ویژه را محاسبه میکند. روش دیگر برای مرحله ۲ از ایدهآلگوریتمهای ویژه تقسیم و تسخیر استفاده میکند (Trefethen & Bau III 1997، سخنرانی ۳۱).
یک روش جایگزین وجود دارد که صریحاً از تجزیه مقادیر ویژه استفاده نمیکند. معمولاً مسئلههای مقدار تکین یک ماتریس M به یک مسئله مقادیر متقارن معادل مانند یا یا
تبدیل میشوند.
رویکردهایی که از تجزیه مقادیر ویژه استفاده میکنند بر اساس الگوریتم QR هستند که به خوبی توسعه یافتهاند تا پایدار و سریع باشند. توجه داشته باشید که مقادیر منحصر به فرد حقیق راست و بردار چپ برای ایجاد دگرگونی هایتشابه لازم ندارند. میتوان بهطور متناوب بین تجزیه QR و تجزیه LQ برای یافتن ماتریس قطری حقیقی هرمتی تکرار ایجاد کند. تجزیه QR به M ⇒ Q R میدهد و تجزیه LQ از R به *R ⇒ L P میدهد؛ بنابراین، در هر تکرار، *M ⇒ Q L P را داریم، M ⇐ L را متعامد و تکرار میکند. سرانجام، این تکرار بین تجزیه QR و تجزیه LQ باعث تولید ماتریسهای واحد چپ و راست میشود. این روش به آسانی قابل تسریع نیست، چرا که این الگوریتم ممکن است دچار تغییر در طیف و شکل گردد. دلیل این امر این است که روش تغییر بدون استفاده از تبدیل شباهت به راحتی تعریف نمیشود. با این حال، این رویکرد تکراری برای اجرا بسیار ساده است، بنابراین وقتی سرعت اهمیتی ندارد ، انتخاب خوبی است.
نتیجه تحلیلی تجزیه مقدار تکین ۲ × ۲
مقادیر متکین یک ماتریس ۲ × ۲ را میتوان به صورت تحلیلی یافت. بگذارید ماتریس M به صورت زیر باشد:
که در آن که اعداد مختلط هستند، و I ماتریس واحد و در نهایت مقادیر نمایانگر ماتریس پاولی میباشند؛ که نهایتاً دو مقدار ویژهٔ آن بهصورت زیر محاسبه میگردد:
محاسبه SVD به کمک نرمافزار متلب
به کمک نرمافزار متلب میتوان SVD یک ماتریس را محاسبه کرد.
دستور (svd(A مقادیر ویژه ماتریس A را بدست میدهد و با استفاده از دستور [u s v] = svd[A] ماتریسهای متعامد و ماتریس مقادیر ویژه، به شما نمایش داده میشود.
مثالها
ماتریس زیر را در نظر میگیریم:
تجزیهٔ مقدارهای منفرد این ماتریس برای UΣV∗ به صورت زیر است:
توجه داشته باشید که Σ خارج از خط مورب صفر (خاکستری ایتالیک) است و یک عنصر مورب صفر (قرمز پررنگ) است. علاوه بر این، به دلیل اینکه ماتریسهای U و V∗ یکتا هستند، ضرب آنها توسط ترانهاده مزدوج آنها ضرب میشود، همانطور که در زیر نشانداده شدهاست. در این حالت، به دلیل اینکه U و V∗ حقیقی هستند، هر کدام یک ماتریس متعامد هستند.
در حالت خاص در صورتی که به صورت زیر انتخاب شود این تقسیم دیگر منحصر به فرد نیست.
همچنین یک تقسیم معتبر ارزش ویژه است.
کاربردهای تجزیه مقادیر منفرد
Pseudo-Inverse
تجزیه مقدار تکین میتواند برای محاسبه شبکه معکوس ماتریس مورد استفاده قرار گیرد. در واقع، شبه معکوس ماتریس M با تجزیه مقدار تکین به صورت زیر است:
شبه معکوس مقدار است، که با جایگزین کردن هر مقدار قطری غیر صفر توسط تابع آن و انتقال ماتریس حاصل ایجاد میشود. pseudoinverse یکی از راه حلهای مسئله حداقل مربعات خطی است.
حل معادلات خطی همگن
یکی از کاربردهای این روش حل دستگاه معادلات است که در سه حالت میتواند بررسی گردد. ماتریس A با ابعاد M*N را درنظر بگیرید. حالتهای زیر ممکن است رخ دهد:
- M= N؛ که تعداد معادلات و مجهولات برابر و روابط خطی هستند.
- M<N؛ تعداد معادلات از مجهولات کمتر است وSVD قابلیت حل آن را دارد.
- M>N؛ در این صورت با دسته معادلات خطی حداقل مربعات سروکار داریم، با روش SVD قابلیت پیدا کردن جواب ممکن است.
مجموعه ای از معادلات خطی همگن را میتوان به عنوان Ax = ۰ برای یک ماتریس A و بردار x نوشت. یک حالت معمول این است که A مشخص بوده و x غیر صفر تعیین میگردد که معادله را ارضا میکند. چنین x متعلق به فضای تهی A است و گاهی اوقات یک بردار تهی A (بردار راست) A نامیده میشود. بردار x را میتوان به عنوان یک بردار است تکین که مطابق با مقدار تکین A که صفر است، توصیف کرد. این مشاهده به این معناست که اگر A یک ماتریس مربعی باشد و هیچ مقدار تکین اضمحلالی نداشته باشد، در نتیجه معادلات هیچ X غیر صفری به عنوان جواب ندارند. همچنین به این معنی است که اگر چندین مقدار تکین اضمحلالی وجود داشته باشد، هر ترکیب خطی از بردارهای تکین راست مربوطه یک جواب برای این دسته از معادلات خواهند بود.
کمینه حداقل مربعات
مسئله حداقل مربعات به تعیین مقدار بردار X که نرم دوم بردار Ax را با قید کمینه میکند اشاره دارد. به نظر میرسد که جواب یک بردار راست تکین A میباشد که به کوچکترین مقدار تکین مربوط میشود.
مجموع مربعات مقادیر منفرد باید برابر با واریانس کلی در A باشد؛ بنابراین، اندازه هر یک از این مقادیر بیان میکند که چه مقدار از واریانس کلی برای هر بردار منفرد محاسبه میشود.
محدوده، فضای تهی و مرتبه
کاربرد دیگر SVD این است که یک نمایش صریح از دامنه و فضای تهی ماتریس M را فراهم میکند. بردارهای تکین راست متناظر با مقادیر کوچک M نمایانگر فضای تهی M و بردارهای تکین چپ متناظر با مقادیر تکین غیر صفر M هستند که محدوده M را شکل میدهند. به عنوان مثال، در مثال بالا فضای تهی توسط دو ستون آخر V پوشانده شده و دامنه توسط سه ستون اول U پوشانده میشود.
در نتیجه، درجه M برابر است با مقادیر تکین غیر صفر که برابر با تعداد عناصر قطری غیر صفر در Σ است. در جبر خطی عددی از مقادیر تکین میتوان برای تعیین رتبه مؤثر یک ماتریس استفاده کرد، چرا که خطا گرد کردن ممکن است به مقادیر کوچک اما غیر صفر در مرتبه ماتریس منجر شوند.
تقریب ماتریس درجه پایین
در برخی از کاربردهای عملی نیاز به حل مسئله تقریب یک ماتریس مانند به ماتریس برای مثال ماتریس کسر شده، داریم که مرتبهٔ آن r است. در حالتی که تقریب ما کاهش نرم فوربینوسی اختلاف دو ماتریس با این قید باشد که مرتبه ماتریس دوم r باشد، جواب از روش SVD حاصل میگردد:
پردازش سیگنال
روش تجزیه مقدار تکین و شبه معکوس با موفقیت برای پردازش سیگنال، پردازش تصویر و دادههای بزرگ (به عنوان مثال، در پردازش سیگنال ژنومی) استفاده شدهاند.
کاهش داده
کاهش داده یا دادهکاوی (به انگلیسی: Data Mining)، به مفهوم استخراج اطلاعات نهان یا الگوها و روابط مشخص در حجم زیادی از دادهها در یک یا چند بانک اطلاعاتی بزرگ گفته میشود. بسیاری از مردم داده کاوی را مترادف واژههای رایج کشف دانش در پایگاهدادهها (به انگلیسی: knowledge discovery in databases) (اختصاری KDD) میدانند. دادهکاوی، پایگاهها و مجموعه حجیم دادهها را در پی کشف و استخراج، مورد تحلیل قرار میدهد. اینگونه مطالعات و کاوشها را به واقع میتوان همان امتداد و استمرار دانش کهن و همه جا گیر آمار دانست. تفاوت عمده در مقیاس، وسعت و گوناگونی زمینهها و کاربردها، و نیز ابعاد و اندازههای دادههای امروزین است که شیوههای ماشینی مربوط به یادگیری، مدلسازی، و آموزش را طلب مینماید.
یکی چالشهای متداول در یادگیری ماشین، وجود چند صد متغیر است، در حالی که بسیاری از الگوریتمهای یادگیری ماشین، اگر با تعدادی بیش از یک مقدار مشخص متغیر کار کنند، با شکست مواجه میشوند. این موضوع، استفاده از تجزیه مقادیر تکین را برای کاهش متغیر در یادگیری ماشین ضروری میکند.
اگر تعداد و انواع مناسبی از ویژگیها برای حل یک مسئله خاص به الگوریتمهای یادگیری ماشین داده شود، این الگوریتمها به خوبی کار میکنند. اما، در صورتی که تعداد ویژگیها (متغیرها) بسیار زیاد باشد، اغلب الگوریتمهای یادگیری ماشین در حل مسئله دچار مشکل میشوند، زیرا با مسئله «دادههای ابعاد بالا» (High Dimensional Data) مواجه خواهیم بود. در اینجا است که بحث «کاهش ابعاد» (Dimensionality Reduction) مطرح میشود. ویژگی (Feature) یا بُعد (Dimension) در واقع پایهٔ بسیاری از عملیاتِ دادهکاوی و یادگیریماشین است.
از طرفی بیان کردیم که که چگونه یک SVD با کاهش تعداد مقادیر تکین میتواند یک ماتریس را بسیار دقیق تقریب بزند. از این ویژگی میتوان برای فشردهسازی دادهها با فرمهای کوتاه شده UU, SS و VV به جای AA و برای کاهش متغیر از جایگزینی AA با UU استفاده کرد. البته در پایان، بر اساس معادله (۴) باید با ضرب SS و VV نتایج را به دستگاه مختصات اصلی تبدیل کرد.
کاربرد SVD در علم سیالات
از جمله کاربردهای این روش در علم مکانیک سیالات را میتوان به موارد زیر اشاره کرد.
- تحلیل دادههای آزمایشگاهی و کاهش داده
- کاهش میزان اغتشاشات تصویر برداری سیال
- یافتن مدالهای انرژی جریان آشفته
- فیلتر اغتشاشات موج صوتی ناشی از حرکت سیال تراکم پذیر
- استخراج انرژی و انستروفی سیال از دادهٔ خروجی تصویر برداری PIV و DPIV
جستارهای وابسته
منابع
پیوند به بیرون
- بعضی تجزیههای مفید در جبر خطی عددی و کاربرد آنها، توسط بهروز خاوری
- مقایسهٔ روشهای پایدارسازی مستقیم و تکراری در پایدارسازی مسئلهٔ انتقال به سمت پایین تعیین ژئوئید، عبدالرضا صفری، و یحیی الله توکلی، مجلهٔ فیزیک زمین و فضا، دورهٔ ۳۴، شمارهٔ ۱، ۱۳۸۷، صفحهٔ ۱۰۸–۸۹