شناسایی دور
در علوم کامپیوتر تشخیص دور (به انگلیسی: Cycle detection) یا یافتن دور (به انگلیسی: cycle finding) مسئلهای الگوریتمی است که به بررسی پیدا کردن یک دور (تکرار) در توالی مقادیر یک تابع میکند.
برای هر تابع f که یک مجموعه متناهی S را به خودش، و هر مقدار اولیه x0 در S را، با توالی مقادیر تابع به صورت زیر نگاشت میکند
در نهایت مجبور به دو بار استفاده کردن از یک مقدار هستیم: باید جفت اندیسهای مجزایی وجود داشته باشد به صورت i و j بهطوریکه xi = xj. هنگامی که این اتفاق میافتد، توالی باید همچنان به صورت دورهای، با همان دنبالهای از مقادیر از xi تا xj − 1 تکرار شود. شناسایی دور مسئله پیدا کردن i و j با دانستن f و x0 میباشد.
چندین الگوریتم برای پیدا کردن دور به سرعت و با استفاده از حافظه اندک شناخته شدهاست. الگوریتم «لاکپشت و خرگوش» فلوید، الگوریتم حرکت دو اشاره گر در توالی مقادیر تابع با دو سرعت متفاوت میباشد تا در نهایت هر دو اشارهگر به یک مقدار برابر اشاره کنند. الگوریتم «برنت» بر اساس ایده جستجوی نمایی برقرار است. هر دو الگوریتم فلوید و برنت از تعداد ثابتی از سلولهای حافظه استفاده میکنند، و هم چنین تعدادی از مقایسه و ارزیابی میان مقادیر تابع که متناسب با فاصله اولین تکرار از شروع توالی میباشد. دیگر الگوریتمها استفاده بیشتر از حافظه در مقابل مقایسههای کمتر را پیشنهاد میدهند.
شناسایی دور شامل تست کیفیت مولد اعداد شبه تصادفی و تابع درهمساز رمزنگارانه، الگوریتم های نظریه اعداد رایانشی، تشخیص حلقه بینهایت در برنامههای کامپیوتری و پیکربندیهای متناوب در اتوماتای سلولی،و داده ساختارهای لیست پیوندی است.
مثال
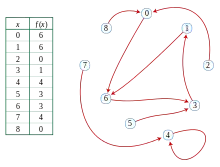
این شکل یک تابع f که مقادیر مجموعه را مینگارد نشان میدهد
{S= {۰٬۱٬۲٬۳٬۴٬۵٬۶٬۷٬۸
را به خود. اگر یکنفر از x0 = ۲ شروع کند و مکرراً f را مورد اعمال قرار دهد دنبالهای از مقادیر زیر را مشاهده میکند
- ۲, ۰, ۶, ۳, ۱, ۶, ۳, ۱, ۶, ۳, ۱, ....
- در این دنباله دور مورد نظر اعداد ۶٬۳٬۱ میباشند
تعاریف
S را مجموعه متناهی دلخواهی فرض کنید، f تابعی دلخواه از S به خودش، و x0 هر عنصر دلخواه از Sباشد. برای هر i> 0، فرض میکنیم xi = f(xi − 1). فرض میکنیم μ کوچکترین اندیسی باشد بهطوریکه مقدار xμ بهطور بینهایت در دنباله مقادیر xi ظاهر شود، و فرض میکنیم λ (طول دور) باشد کوچکترین عدد صحیح مثبت باشد بهطوریکه xμ = xλ + μ. تشخیص دور مسئله یافتن λ و μ میباشد.[1]
همین مسئله را در نظریه گراف،با ساخت یک گراف تابع (که یک گراف جهت دار خوانده میشودد که در آن هر راس دارای یک یال خارج شونده است) که رئوس آن عناصر S و یالهای آن یک عنصر را به مقدار تابع مربوط به آن نگاشت میکنند، همانطور که در شکل نشان داده شدهاست. مجموعه رئوس قابل دسترسی با شروع از راس x0 از یک زیر گراف با یک شکل شبیه رو (ρ): یک مسیر با طول μ از x0 به یک دور با λ راس.[2]
بیان کامپیوتری
بهطور کلی، f را نمیتوان به صورت جدولی از مقادیر، طوریکه در شکل بالا نشان داده شده نمایش داد. بلکه، یک الگوریتم تشخیص دور ممکن است یا با دنباله مقادیر xi، یا یک تابع برای محاسبه f داده شود. هدف پیدا کردن λ و μ با بررسی چند مقدار از دنباله یا پیدا کردن مقدار تابع در چند مرتبه با کمترین استفاده از سلولهای حافظه میباشد. بهطور معمول، پیچیدگی فضا در مسئله تشخیص دور اهمیت دارد: ما مایل به حل این مسئله با استفاده ماز مقداری از حافظه هستیم که کمتر از حافظه مورد نیاز برای ذخیره کل دنباله اعداد میباشد.
در برخی از برنامهها، و به ویژه در الگوریتم رو پولارد برای تجزیه اعداد طبیعی،الگوریتم دسترسی محدودتری به S و f دارد. در الگوریتم پولارد، به عنوان مثال، S مجموعهای از اعداد صحیح میباشد که عامل اول عدد مورد تجزیه به آن بخشپذیر است، بنابراین حتی اندازه S هم نامعلوم است. برای اینکه تشخیص دور با چنین اطلاعات محدودی قابل استفاده باشد، باید براساس تواناییهای زیر بنا شوند. در ابتدا فرض میشود الگوریتم حافظه مخصوص به خود را دارد که یک نشانگر به مقدار شروع یعنی x0 دارد. در هر مرحله ممکن است یکی از سه عمل زیر را انجام دهد: ممکن است هر نشانگری را به شئ دیگری کپی کند، ممکن است f را اعمال کند و هرکدام از نشانگرهایش را با یک نشانگر به شئ بعدی جایگزین کند یا ممکن است با اجرای یک تابع تشخیص دهد که دو نشانگر به یک مقدار برابر در دنباله اشاره دارند یا نه. آزمون برابری میتواند بعضی از محاسبات غیربدیهی دربرداشته باشد: برای مثال، در الگوریتم پولارد رو، این عملیات اینگونه پیاده میشود که آیا اختلاف بین دو مقدار ذخیره شده بزرگترین مقسوم علیه مشترک بغیر بدیهی با عدد مورد تجزیه دارد یا خیر. در این زمینه، با قیاس با مدل محاسباتی ماشین اشاره گر، یک الگوریتم که تنها از کپی کردن یک اشاره گر، پیشروی در دنباله، و آزمونهای برابری استفاده میکند، الگوریتم اشارهگری نامیده میشود.
الگوریتمها
اگر ورودی به عنوان یک رابطه برای محاسبه f داده شده باشد، مسئله تشخیص چرخه ممکن است بهطور بدیهی با تنها λ + μ اجرای تابع حل شود، به سادگی با محاسبه دنبالهای از مقادیر xi و با استفاده از یک ساختار دادهمانند یک جدول درهم ساز برای ذخیره این مقادیر و تست اینکه آیا هر مقدار در حال حاضر ذخیره شدهاست یا خیر. اما پیچیدگی فضایی این الگوریتم متناسب با λ + μ، بهطور بیارزشی بزرگ است. علاوه بر این برای اجرای این روش به عنوان یک الگوریتم اشارهگر، نیاز به استفاده از آزمون برابری برای هر جفت از مقادیر و در نتیجه به زمان از مرتبه دو میانجامد؛ بنابراین تحقیقات در این زمینه بر روی دو هدف متمرکز شده: استفاده از فضای کمتر از این الگوریتم ساده، و پیدا کردن الگوریتمهای اشارهگری که با استفاده از آزمون برابری کمتر.
الگوریتم فلوید
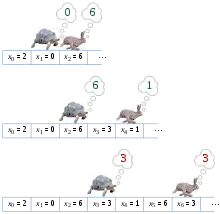
الگوریتم یافتن دور فلوید الگوریتمی است که از دو اشارهگر استفاده میکند، که با سرعتهای متفاوت در دنباله حرکت میکنند. همچنین به نام «الگوریتم لاکپشت و خرگوش» نامیده میشود با اشاره به حکایت لاکپشت و خرگوش از ازوپ.
الگوریتم پس از نام رابرت فلوید با اعتبار اختراع آن توسط دانلد کنوت نامگذاری شد.[3][4] با این حال به نظر نمیرسد این الگوریتم در کارهای منتشر شده از فلوید باشد، و این ممکن است یک سوءتفاهم باشد: فلوید توصیف الگوریتم را با لیست کردن تمامی دورها در یک گراف جهت دار سال ۱۹۶۷ سال در یک مقاله انجام داد،[5] اما این مقاله مسئله یافتن دور در یک گراف تابعی که موضوع این مقاله است را شرح نداد. در واقع بیانیه کنوت (در سال ۱۹۶۹)، و نسبت دادن آن به فلوید، بدون استناد، اولین ظهور آن بهطور چاپی است و آن را در نتیجه ممکن است یک قضیه منتسب به یک فرد است.[6]
نکته اصلی در درک این الگوریتم این است که، برای هر عدد صحیح i ≥ μ و k ≥ ۰ داریم xi = xi + kλکه در آن λ طول حلقه یافت شده و μ اندیس اولین عنصر چرخه است. بهطور خاص، i = kλ ≥ μاگر و تنها اگر xi = x2i. این الگوریتم تنها نیاز به بررسی مقادیر تکراری این فرم خاص، تا آنجا که یکی از مقادیر پس از شروع دنباله تکرار شود، برای یافتن دوره تناوبv برای تکرار که مضربی از λ میباشد. به محض اینکه v یافت شد، الگوریتم دنباله را دوباره از آغاز بررسی میکند تا اولین مقدار تکراری xμ، با توجه به این مسئله کهv بر λ بخشپزیر است به همین دلیل xμ = xμ + v. سرانجام پس از یافتن مقدار μ بهطور بدیهی به دنبال طول λ میگردیم که کوچکترین طول دور میباشد، با یافتن اولین مکان μ + λ که در آن xμ + λ = xμ.
این الگوریتم در نتیجه دو اشاره گر را در طول دنباله داده شده حفظ میکند، یکی (لاکپشت) در xiو دیگری (خرگوش) در x2i. در هر مرحله از الگوریتم،i را با حرکت لاکپشت یک گام به جلو یک واحد افزایش میدهد و خرگوش دو گام به جلو در دنباله، و سپس مقدار دنباله در این دو اشاره گر را مقایسه میکند. کوچکترین مقدار i > 0 که در آن نقطه مقدار لاکپشت و خرگوش برابر است که مقدار ν مورد نظر ماست.
کد پایتون زیر این ایده به عنوان یک الگوریتم پیادهسازی میشود:
def floyd(f, x0):
# Main phase of algorithm: finding a repetition x_i = x_2i.
# The hare moves twice as quickly as the tortoise and
# the distance between them increases by 1 at each step.
# Eventually they will both be inside the cycle and then,
# at some point, the distance between them will be
# divisible by the period λ.
tortoise = f(x0) # f(x0) is the element/node next to x0.
hare = f(f(x0))
while tortoise != hare:
tortoise = f(tortoise)
hare = f(f(hare))
# At this point the tortoise position, ν, which is also equal
# to the distance between hare and tortoise, is divisible by
# the period λ. So hare moving in circle one step at a time,
# and tortoise (reset to x0) moving towards the circle, will
# intersect at the beginning of the circle. Because the
# distance between them is constant at 2ν, a multiple of λ,
# they will agree as soon as the tortoise reaches index μ.
# Find the position μ of first repetition.
mu = 0
tortoise = x0
while tortoise != hare:
tortoise = f(tortoise)
hare = f(hare) # Hare and tortoise move at same speed
mu += 1
# Find the length of the shortest cycle starting from x_μ
# The hare moves one step at a time while tortoise is still.
# lam is incremented until λ is found.
lam = 1
hare = f(tortoise)
while tortoise != hare:
hare = f(hare)
lam += 1
return lam, mu
این کد تنها به دنباله با ذخیرهسازی و کپی کردن اشاره گرها، مقداریابی تابع و آزمون برابری دسترسی دارد؛ بنابراین، آن را به عنوان یک الگوریتم اشارهگری مینامیم. این الگوریتم از O(λ + μ) عملیات از این نوع و O(1) فضای ذخیرهسازی استفاده میکند.[7]
الگوریتم برنت
ریچارد پیرس برنت یک الگوریتم یافتن دور جایگزین را توصیف میکند، که همانند الگوریتم لاکپشت و خرگوش تنها نیاز به دو اشاره گر در دنباله دارد.[8] با این حال، بر اساس اصل مختلف دیگری بنا شدهاست: جستجو برای کوچکترین توان دو 2i که بزرگتر از هر دو λ و μ باشد. برای i = ۰, ۱, ۲, ...، الگوریتم x2i−1 را با هر یک از مقادیر پس از آن دنباله مقایسه میکند، و هر گاه عدد مورد نظر را یافت متوقف میشود. این الگوریتم نسبت به الگوریتم لاکپشت و خرگوش دو مزیت دارد: مقدار صحیح λ برای دور را بهطور مستقیم مییابد به جای اینکه نیاز به جستجو برای آن در مرحله بعدی داشته باشد، و مراحل آن شامل تنها یک مقداریابی از f میباشد.[9]
کد پایتون زیر با جزییات نشان میدهد این تکنیک چگونه کار میکند.
def brent(f, x0):
# main phase: search successive powers of two
power = lam = 1
tortoise = x0
hare = f(x0) # f(x0) is the element/node next to x0.
while tortoise != hare:
if power == lam: # time to start a new power of two?
tortoise = hare
power *= 2
lam = 0
hare = f(hare)
lam += 1
# Find the position of the first repetition of length λ
mu = 0
tortoise = hare = x0
for i in range(lam):
# range(lam) produces a list with the values 0, 1, ... , lam-1
hare = f(hare)
# The distance between the hare and tortoise is now λ.
# Next, the hare and tortoise move at same speed until they agree
while tortoise != hare:
tortoise = f(tortoise)
hare = f(hare)
mu += 1
return lam, mu
مانند الگوریتم لاکپشت و خرگوش، این یک الگوریتم اشارهگری است که از O(λ + μ) تست و مقدار یابی تابع و O(1) فضای ذخیرهسازی استفاده میکند.
سخت نیست که نشان دهیم تعداد مقداریابیهای تابع نسبت به الگوریتم فلوید هیچگاه بیشتر نمیشود. برنت ادعا میکند که بهطور متوسط الگوریتم یافتن دور او حدود ۳۶ درصد سریعتر از الگوریتم فلوید میباشد و الگوریتم پولارد رو را تا حدود ۲۴٪ تسربع میکند. او همچنین یک آنالیز حالت متوسط برای یک نسخه تصادفی الگوریتم اجرا کرد که در آن دنبالهای از شاخضهای دنبال شده خود توانی از ۲ نبودند اما یک مضربی از توان دو به صورت تصادفی بودند. اگرچه برنامه اصلی او در رابطه با تجزیه عوامل اول اعداد صحیح بود، برنت همچنین در رابطه با برنامه تست کردن اعداد شبه تصادفی نیز بحث کرد.
الگوریتم گسپر
الگوریتم گسپر[10][11] دوره تناوب را مییابد اما نقطه شروع اولین پریود را مشخص نمیکند. از ویژگیهای اصلی آن است که هیچگاه برای مقداریابی تابع مولد بر نمیگردد که این عمل از نظر زمانی و حافظه بهینه است.
بررسی زمان و حافظه
برخی از نویسندگان روشهایی را مورد بررسی قرار دادهاند که نسبت به الگوریتم فلوید و برنت حافظهٔ بیشتری نیاز دارد اما دور را سریعتر شناسایی میکند. بهطور کلی این روشها دنبالهای از مقادیر از پیش محاسبهشده را ذخیره میکنند، و بررسی میکنند که آیا مقادیر جدید ما مقادیر قبلاً محاسبه شده برابرند یا خیر. به منظور انجام سریع آنها، بهطور معمول از یک جدول درهمسازی یا یک داده ساختار مشابه برای ذخیره مقادیر از قبل محاسبه شدهاستفاده میشود، و در نهایت هیچ الگوریتم اشارهگری در کار نیست: بهطور خاص آنها قابل پیاده شدن به روی الگوریتم پولارد نیستند. تفاوتی که این الگوریتمها دارند در این است که کدام مقادیر برای ذخیره شدن انتخاب شوند. ما به بررسی این روشها بهطور خلاصه میپردازیم:
- مدلهای مختلف روش برنت به این صورت است که اندیسهای دنبالههای ذخیره شده توانی از یک عدد نزدیک به یک R به غیر از ۲ باشد. با انتخاب R به عنوان عددی نزدیک به یک، و ذخیره کردن دنباله مقادیری که اندیسهایشان نزدیک به دنباله توانهای R میباشد، یک الگوریتم تشخیص دور میتواند از تعدادی از مقایسهها از میان عوامل λ + μ استفاده کند.[12][13]
- Sedgewick, Szymanski و Yao روشی ارائه دادند که به M سلول از حافظه نیاز دارد و در بدترین حالت به مقداریابی تابع برای برخی مقادیر ثابت c نیاز دارد، که نشاندهنده بهینگی است. این روش شامل حفظ یک پارامتر عددی مانند d، ذخیره کردن مکانهایی از دنباله که مضربی از d میباشند در یک جدول، و پاک کردن جدول و دو برابر کردن مقدار d هر زمان که مقادیر زیادی ذخیره شد.
- تعدادی از نویسندگان روشهای نقاط متمایز را توصیف کردهاند که مقادیر تابع را در یک جدول بنابر معیارهایی مثل مقدار آنها (به حای مکان آنها) ذخیره میکنند. برای مثال، برای بعضی مقادیر d چون بر صفر بحشپذیر هستند مقادیر مساوی با صفر ذخیره میشوند[14].[15] بهطور سادهتر ،Nivasch با اعتبار دادن به Woodruff با پیپشنهاد ذخیره کردن تصادفی مقادیری که قبلاً مشاهده شده، اقدام به انتخاب یک عدد تصادفی مناسب کند تا نمونه بهطور تصادفی باقی بماند.
- Nivasch الگوریتمی را توصیف میکند که از مقدار حافظه معین و ثابت استفاده نمیکند اما مقدار حافظه مورد انتظارش (تحت این فرض که ورودی تابع تصادفی میباشد) به صورت لگاریتمی از طول دنباله میباشد. در این روش یک بخش زمانی در جدول حافظه ذخیره میشود بهطوریکه هیچکدام از بخشهای بعدی مقدار کوچکتری از آن نداشته باشند. همانطور که Nivasch نمایش داد، میتوان آیتمهای این روش را با استفاده از داده ساحتار پشته حفظ کرد، و در برای هر عضو متوالی دنباله کافی است تنها آن را با عنصر روی پشته مقایسه کنیم. الگوریتم زمانی متوقف میشود که عنصر تکرار شونده با کمترین مقدار یافت شود. با اجرای الگوریتم مشابه در چندین پشته، با استفاده از جایگشتهای تصادفی مقادیر دنباله برای ترتیبهای محتلف آنها در پشته، منجر به یک بهینگی زمانی یا حافظه میشود همانند الگوریتمهای قبلی. حتی نسخهای از این الگوریتم که با یک پشته است یک الگوریتم اشارهگری نیست، با توجه به این که نیاز به مقایسه برای تعیین مقدار کوچکتر از میان دو مقدار را دارد.
هر الگوریتم شناسایی دور که اقدام به ذخیره M مقدار از دنباله ورودی در حافظه میکند، حداقل نیاز به اجرای مقداریابی تابع دارد.[16][17]
کاربردها
شناسایی دور در بسیاری از برنامهها استفاده شدهاست.
- تعیین طول یک مولد اعداد شبه تصادفی یکی از نشانههای قدرت این روش است. این کاربرد برای اولین برا توسط دانلد کنوت هنگامی که الگوریتم فلوید را بررسی میکردهاست بیان شدهاست.
- تعدادی زیادی از الگوریتمهای نظریه اعداد بر پایهٔ این روش بنا شدهاند، به عنوان مثال میتوان از الگوریتم رو پولارد برای تجزیهٔ اعداد نام برد.[18]
- تشخیص دور یکی از روشهای ممکن برای تشخیص حلقه بینهایت در انواع خاص برنامههای کامپیوتری است.[19]
- پیکربندیهای تناوبی موجود در شبیهسازیهای اتوماتای سلولی را میتوان با به کاربردن الگوریتم تشخیص دور در دنبالهای از حالتهای اتوماتون به دست آورد.
پانویس
- Joux, Antoine (2009), Algorithmic Cryptanalysis, CRC Press, p. 223, ISBN 978-1-4200-7003-3 More than one of
|ISBN=and|isbn=specified (help)More than one of|ISBN=and|isbn=specified (help) . - Joux (2009, p. 224).
- Knuth, Donald E. (1969), The Art of Computer Programming, vol. II: Seminumerical Algorithms, Addison-Wesley, p. 7, exercises 6 and 7 More than one of
|author-link=and|authorlink=specified (help)More than one of|authorlink=,|authorlink=, and|author-link=specified (help) - Handbook of Applied Cryptography, by Alfred J. Menezes, Paul C. van Oorschot, Scott A. Vanstone, p. 125, describes this algorithm and others
- Floyd, R.W. (1967), "Non-deterministic Algorithms", J. ACM, 14 (4): 636–644, doi:10.1145/321420.321422 More than one of
|author-link=and|authorlink=specified (help); More than one of|DOI=and|doi=specified (help)More than one of|authorlink=,|authorlink=, and|author-link=specified (help); More than one of|DOI=and|doi=specified (help) - The Hash Function BLAKE, by Jean-Philippe Aumasson, Willi Meier, Raphael C. -W. Phan, Luca Henzen (2015), p. 21, footnote 8
- Joux (2009), Section 7.1.1, Floyd's cycle-finding algorithm, pp. 225–226.
- Brent, R. P. (1980), "An improved Monte Carlo factorization algorithm" (PDF), BIT Numerical Mathematics, 20 (2): 176–184, doi:10.1007/BF01933190 More than one of
|author-link=and|authorlink=specified (help); More than one of|DOI=and|doi=specified (help)More than one of|authorlink=,|authorlink=, and|author-link=specified (help); More than one of|DOI=and|doi=specified (help) . - Joux (2009), Section 7.1.2, Brent's cycle-finding algorithm, pp. 226–227.
- «نسخه آرشیو شده». بایگانیشده از اصلی در ۱۴ آوریل ۲۰۱۶. دریافتشده در ۳۰ مه ۲۰۱۷.
- http://www.inwap.com/pdp10/hbaker/hakmem/flows.html
- Schnorr, Claus P.; Lenstra, Hendrik W. (1984), "A Monte Carlo factoring algorithm with linear storage", Mathematics of Computation, 43 (167): 289–311, doi:10.2307/2007414, JSTOR 2007414 More than one of
|JSTOR=and|jstor=specified (help); More than one of|DOI=and|doi=specified (help)More than one of|JSTOR=and|jstor=specified (help); More than one of|DOI=and|doi=specified (help) . - Teske, Edlyn (1998), "A space-efficient algorithm for group structure computation", Mathematics of Computation, 67 (224): 1637–1663, doi:10.1090/S0025-5718-98-00968-5 More than one of
|DOI=and|doi=specified (help)More than one of|DOI=and|doi=specified (help) . - van Oorschot, Paul C.; Wiener, Michael J. (1999), "Parallel collision search with cryptanalytic applications", Journal of Cryptology, 12 (1): 1–28, doi:10.1007/PL00003816 More than one of
|DOI=and|doi=specified (help)More than one of|DOI=and|doi=specified (help) . - Quisquater, J. -J.; Delescaille, J. -P., "How easy is collision search? Application to DES", Advances in Cryptology – EUROCRYPT '89, Workshop on the Theory and Application of Cryptographic Techniques, Lecture Notes in Computer Science, 434, Springer-Verlag, pp. 429–434
- Fich, Faith Ellen (1981), "Lower bounds for the cycle detection problem", Proc. 13th ACM Symposium on Theory of Computing, pp. 96–105, doi:10.1145/800076.802462 More than one of
|author-link=and|authorlink=specified (help); More than one of|DOI=and|doi=specified (help)More than one of|authorlink=,|authorlink=, and|author-link=specified (help); More than one of|DOI=and|doi=specified (help) . - Allender, Eric W.; Klawe, Maria M. (1985), "Improved lower bounds for the cycle detection problem", Theoretical Computer Science, 36 (2–3): 231–237, doi:10.1016/0304-3975(85)90044-1 More than one of
|DOI=and|doi=specified (help)More than one of|DOI=and|doi=specified (help) . - Pollard, J. M. (1975), "A Monte Carlo method for factorization", BIT, 15 (3): 331–334, doi:10.1007/BF01933667 More than one of
|DOI=and|doi=specified (help)More than one of|DOI=and|doi=specified (help) . - Van Gelder, Allen (1987), "Efficient loop detection in Prolog using the tortoise-and-hare technique", Journal of Logic Programming, 4 (1): 23–31, doi:10.1016/0743-1066(87)90020-3 More than one of
|DOI=and|doi=specified (help)More than one of|DOI=and|doi=specified (help) .
منابع
- مشارکتکنندگان ویکیپدیا. «Cycle detection». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۳۰ مه ۲۰۱۷.
پیوند به بیرون
- گابریل Nivasch سه چرخه تشخیص مشکل و پشته و الگوریتم
- لاکپشت و خرگوش, Portland, الگوی Repository
- فلوید چرخه الگوریتم تشخیص (لاکپشت و خرگوش)
- برنت چرخه الگوریتم تشخیص (Teleporting لاکپشت)
