ارتفاع (مثلث)
ارتفاع یک مثلث در هندسه عبارت است از پارهخطی که از یک رأس آغاز میشود و بر ضلع مقابل مثلث (یا امتداد آن) عمود است (زاویه قائمه تشکیل میدهد). محل برخورد ارتفاع با قاعده یا امتداد آن، پای عمود نام دارد. معمولاً به طول ارتفاع همان ارتفاع گفته میشود که برابر است با فاصلهٔ میان رأس و قاعده (یا قاعدهٔ امتدادیافته).
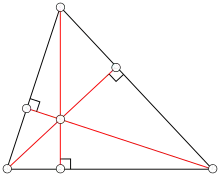
از ارتفاع در محاسبهٔ مساحت مثلث استفاده میشود که برابر است با نصف حاصل ضرب طول ارتفاع در قاعدهٔ آن. در نتیجه بلندترین ارتفاع به کوتاهترین قاعدهٔ مثلث عمود میشود. ارتفاع مثلث به مبحث توابع مثلثاتی نیز مرتبط است. یکی از ارتفاعهای مثلث منفرجه، بیرون شکل است
قضیههای مرتبط
ارتفاع و پیرامون مثلث
برای هر مثلثی با اضلاع a, b، c و نصف محیط برابر با s = (a+b+c) / 2 طول ارتفاع رسم شده از رأس a برابر است با:
این نتیجه از فرمول هرون بدست آمد.
دایرهٔ محاطی
فرض کنید مثلثی با اضلاع a, b، c و ارتفاعهای ha, hb, و hc داریم. اگر شعاع دایرهٔ محاطی را r بنامیم، رابطهٔ زیر برقرار خواهد بود:
دایرهٔ محیطی
اگر ارتفاع رسم شده از یک رأس را ha، دو ضلع دیگر را به ترتیب b و c و شعاع دایرهٔ محیطی را R بنامیم. آنگاه داریم:[1]:p. 71
نقطهٔ درونی
اگر p1, p2, و p3 به ترتیب فاصلهٔ نقطهٔ دلخواه P از اضلاع مثلث باشند و h1, h2, و h3 شعاعهای متناظر باشند، آنگاه رابطهٔ زیر درست خواهد بود:[1]:p. 74
مساحت
اگر ارتفاعهای رسم شده از رأسهای a, b و c به ترتیب , , و باشند با فرض داشتن ، رابطهٔ زیر برقرار خواهد بود:[2]
مثلث متساوی الاضلاع
برای هر نقطهٔ دلخواه P در یک مثلث متساویالاضلاع، مجموع خطهای عمود رسم شده از آن نقطه بر روی اضلاع مثلث برابر است با طول ارتفاع مثلث. به این مطلب، قضیهٔ ویویانی میگویند.
مثلث قائمالزاویه
در یک مثلث قائمالزاویه، با فرض ارتفاعهای ha, hb, و hc (واضح است که دو ارتفاع خود همان دو ضلع مثلث اند) رابطهٔ زیر میان سه ارتفاع مثلث برقرار است:[4][5]
مرکز ارتفاعی
به محل همرسی ارتفاعها مرکز ارتفاعی مثلث گویند(). خط اویلر مثلث از مرکز ارتفاعی نیز میگذرد.
مثلث پادک
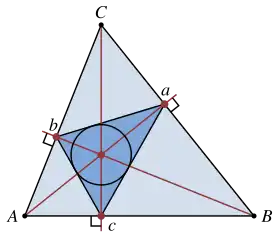
اگر محل برخورد ارتفاعها با اضلاع بهترتیب باشد، مثلث مثلث پادک میگوییم. ارتفاعهای مثلث، نیمسازهای مثلث پادک هستند، و مرکز ارتفاعیِ مثلث، مرکز دایره محاطی مثلث پادک است.
جستارهای وابسته
منابع
- Johnson, Roger A. , Advanced Euclidean Geometry, Dover Publ. , 2007 (orig. 1929).
- Mitchell, Douglas W. , "A Heron-type formula for the reciprocal area of a triangle," Mathematical Gazette 89, November 2005, 494.
- Alfred S. Posamentier and Charles T. Salkind, Challenging Problems in Geometry, Dover Publishing Co. , second revised edition, 1996.
- Voles, Roger, "Integer solutions of ," Mathematical Gazette 83, July 1999, 269–271.
- Richinick, Jennifer, "The upside-down Pythagorean Theorem," Mathematical Gazette 92, July 2008, 313–317.
