ابرمکعب
در هندسه، اَبَرمکعب یا فوقمکعب همتای اِن-بعدی مربع (اِن=۲) و مکعب (اِن=۳) است. فوق مکعب، یک شکل محدب، فشرده و بسته است که از دو گروه پارهخط موازی با طول یکسان تشکیل شده که در همهٔ ابعاد فضا بر یکدیگر عمود هستند. اَبَرمکعب با نام اِن-مکعب (n-cube) نیز شناخته میشود.
 |
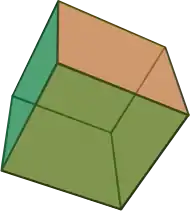 |
| تسرکت (ابرمکعب چهار بعدی) | مکعب (ابرمکعب سه بعدی) |
|---|
یک ابرمکعب حالت خاصی از اَبَرمکعبمستطیل (hyperrectangle) (که با نام ارتوتوپ (orthotope) نیز شناخته میشود) است.
یک ابرمکعب واحد، یک فوقمکعب با طول ضلع ۱ است.
ساخت

۰-یک نقطه، یک اَبَرمکعب با بعد صفر است. (یعنی نقطه را میتوان نوعی فوقمکعب در فضای در نظر گرفت)
۱-اگر این نقطه به اندازهٔ یک واحد به سمتی، حرکت کند، یک پارهخط پدید میآورد. پارهخط یک اَبرمکعب با بعد یک است. (به بیان دیگر پارهخط نوعی فوقمکعب در فضای است.)
۲-اگر این پارهخط در جهت عمود بر طول خودش، به اندازه یک واحد جابجا شود، یک مربع دوبعدی پدید میآورد. (این مربع، یک ابرمکعب در فضای خواهد بود.)
۳-اگر این مربع به اندازهٔ یک واحد، در راستای عمود بر سطح خودش، جابجا شود، یک مکعب سهبعدی پدید خواهد آمد (ابرمکعبی در فضای ریاضی ).
۴-اگر این مکعب در بُعد چهارم به اندازهٔ یک واحد، جابجا شود، یک تسرکت چهاربعدی بهدست خواهد آمد. (تسرکت یک ابرمکعب در فضای است.)

این شیوه در باره فضای اِن-بعدی، و دستیابی به ابرمکعبهای اِن-بعدی نیز قابل گسترش است.
این فرایند حرکت بر امتداد عمود بر شیء، میتواند به شیوهٔ ریاضی با جمع مینکوفسکی بیان شود.
ابرمکعب dبعدی، یک جمع مینکوفسکی از پارهخطهای دوبدو متعامد شکل گرفته و در نتیجه یک مثال از زونوتوپ است.
از دیدگاه ریختشناسی (توپولوژی) ساختار تک-اسکلتی ابرمکعب یک گراف ابرمکعب است.
مختصات
یک ابرمکعب واحد چندبعدی، یک سطح محدب از نقاط با دگرگونیهای علامت در مختصات کارتزین است . طول هر ضلع آن برابر ۱ و حجمش نیز ۱ واحد است.
همچنین یک ابرمکعب اِن-بعدی اغلب به عنوان رویهٔ محدب تلقی شدهاست . اغلب این فرم بهخاطر سهولت در نوشتن مختصات انتخاب شدهاست. طول لبهٔ آن ۲ و رتبه اِن-بعدیاش نیز است.
منابع
- Bowen, J. P. (April 1982). "Hypercubes". Practical Computing. ۵ (۴): ۹۷–۹۹.
- Coxeter, H. S. M. (1973). Regular Polytopes (3rd ed.). Dover. pp. 123. ISBN 0-486-61480-8. p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n dimensions (n ≥ ۵)
- Hill, Frederick J.; Gerald R. Peterson (1981). Introduction to Switching Theory and Logical Design: Second Edition. NY: John Wiley & Sons. ISBN 0-471-39882-9. Cf Chapter 7.1 "Cubical Representation of Boolean Functions" wherein the notion of "hypercube" is introduced as a means of demonstrating a distance-1 code (Gray code) as the vertices of a hypercube, and then the hypercube with its vertices so labelled is squashed into two dimensions to form either a Veitch diagram or Karnaugh map..
پیوند به بیرون
- Weisstein, Eric W. "ابرمکعب". MathWorld.
- Weisstein, Eric W. "گرافهای ابرمکعب". MathWorld.
- Olshevsky, George, Measure polytope at Glossary for Hyperspace.
- بعد چهارم (Rotation of 4D – ۷D-Cube)
- چرخش یک ابرمکعب by Enrique Zeleny، Wolfram Demonstrations Project.
- ابرمکعب نمایشی استریوسکوپی
- Rudy Rucker and Farideh Dormishian's Hypercube Downloads

