شبکه براوه
شبکه براوه (به انگلیسی: Bravais lattice) آرایه نامحدودی از نقاط گسسته در فضا است که چینش و جهت آن مستقل از نقطهٔ مبدأ باشد و از رابطهٔ زیر پیروی کند:
که در آن niها اعداد صحیح و aiها بردارهای اولیهای هستند که در جهات مختلف شبکه را میسازند.
از این گونه شبکهها به منظور مدلسازی شبکههای بلوری استفاده میشود. از لحاظ هندسی در سه بعد تنها ۱۴ گونه شبکه براوه مستقل میتواند وجود داشته باشد. این ۱۴ گونه، ۱۴ تا از ۲۳۰ گروه فضاییاند و در ۷ دستگاه بلوری دستهبندی شدهاند.
دوبعدی
اگر تنها صفر یا یک بعد را در نظر بگیریم، تنها یک شبکه براوه میتواند وجود داشته باشد.
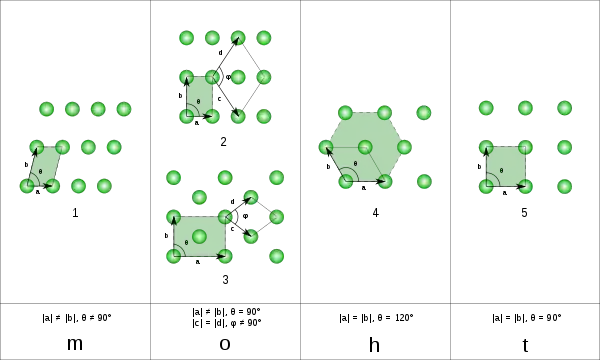
در دوبعد میتوان ۵ گونه شبکه براوه داشت.
سهبعدی
در سه بعد میتوان ۱۴ گونه شبکه براوه داشت که در ۷ دستگاه بلوری دستهبندی شدهاند.سه شبکه مهم که بیشتر ساختارهای بلوری در این شبکهها متبلور میشود مکعبی مرکزحجمی، مکعبی مرکزسطحی، و هگزاگونال هستند.
برای بررسی انواع ساختار های کریستالی مفاهیمی مورد نیاز است که عبارتند از:
عدد همسایگی (coordination number): یکی از پارامترهای کلیدی در توصیف شبکه می باشد که بیانگر تعداد نزدیکترین همسایه(اتم)های هر اتم می باشد.
فاکتور تراکم اتمی (APF):فاکتور تراکم اتمی برای هر شبکه واحد به صورت نسبت حجم اتم های داخل یک سلول واحد به حجم سلول واحد محاسبه می شود.
پارامتر شبکه (Lattice Parameter):مشخصه هایی از سلول واحد می باشد که به کمک آن می توان اندازه و شکل سلول واحد را مشخص کرد. این پارامترها عبارتند از طول اضلاع سلول واحد (a,b,c) و زاویه بین اضلاع یعنی (α,β,γ).
فاصله بین صفحه ای (d):فاصله بین صفحه ای به صورت فاصله بین صفحات موازی متوالی تعریف می شود که برای هر نوع ساختار کریستالی برحسب h,k,l که اندیس میلر می باشند و پارامترهای شبکه قابل محاسبه است.
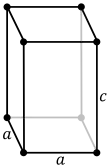
ساختار مکعبی (Cubic)

در این ساختار پارامتر شبکه a , b و c با هم برابر می باشند و تمام زوایا برابر 90 درجه است.
ساختار مکعبی ساده
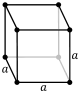
در این ساختار(ساختار مکعبی) شبکه واحد شامل یک اتم میباشد و اتم ها در لبه های مکعب بایکدیگر در تماس هستند.
پارامتر شبکه(a):
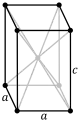
ساختار مکعبی مرکزحجمی(BCC)


در این ساختار، شبکه واحد شامل دو اتم می باشد.
پارامتر شبکه(a):
که در آن R شعاع اتمی می باشد.در این ساختار اتم ها از طریق قطر مکعب با یکدیگر تماس دارند.این ساختار یکی از ساختار های رایج در فلزها است. از جمله موادی که دارای این ساختار می باشند عبارتند از: آهن (در دمای کمتر از 900 درجه سانتیگراد) ،کروم ، تنگستن ، مولیبدن ، تانتالیم.
ساختار مکعبی مرکز سطحی(FCC)

در این ساختار شبکه واحد شامل چهار اتم میباشد.
مقدار APF در این ساختار بیشترین مقدار ممکن برای کره هایی با قطر یکسان می باشد.
پارامتر شبکه(a):
در این رابطه R شعاع اتمی است. در این ساختار اتم ها طریق قطر مربع های وجوه با هم در تماس هستند.این ساختار نیز یکی از ساختار های رایج در فلزات است. از جمله موادی که دارای این ساختار می باشند عبارتند از: آلومینیوم ، مس ، طلا ، سرب ، نیکل ، نقره ، پلاتین و...
ساختار هگزاگونال (Hexagonal)
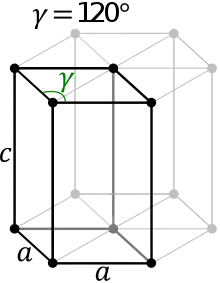
در این ساختار پارامترهای شبکه a و b باهم برابرند اما پارامتر شبکه c مقدار متفاوتی دارد. همچنین زوایای α و β با هم یکسان و برابر 90 درجه است اما زاویه γ برابر 120 درجه می باشد.
ساختار هگزاگونال فشرده (HCP)
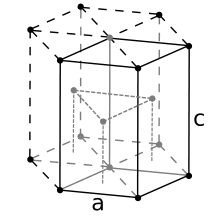
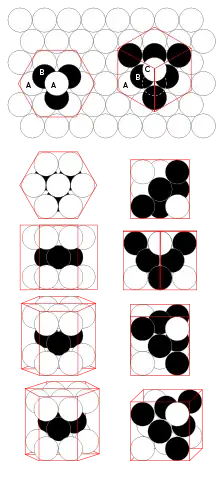
در این ساختار شبکه واحد شامل 6 اتم می باشد و فاکتور تراکم پذیری بیشتری نسبت به ساختار هگزاگونال ساده دارد.ساختار شش وجهی، دارای سه لایه اتمی است. در هر دو طرف بالا و پایین لایهها، 6 اتم وجود دارد که در آرایش شش ضلعی قرار گرفتهاند و در وسط شش ضلعی، اتم هفتم قرار گرفتهاست. لایه میانی دارای سه اتم است که به صورت مثلث مابین دو سطح شش وجهی بالایی و پایینی قرار گرفتهاند. این بدان معنی است که شش اتم شش ضلعی در صفحات بالا و پایین قرار گرفتهاند و فقط سه اتم میانی وجود دارد که مابین آنها قرار میگیرد.
همانطور که مشاهده می شود APF این ساختار و همچنین عدد همسایگی آن با ساختار FCC برابر است.این ساختار نیز یکی از ساختارهای رایج در فلزات می باشد.از جمله موادی که دارای این ساختار می باشند عبارتند از: کادمیوم ، کبالت ، تیتانیوم ، روی. یکی از راههای کارامد برای تصور روش قرار گرفتن اتمهای کروی یک اندازه در ساختار اتمی HCP در نظر گرفتن جانمایی آن در سه بعد است. بهطور مثال، اگر صفحه A زیر صفحه B قرار گیرد، دو طریقه ممکن برای قرار دادن صفحه بعدی روی لایه B وجود دارد. اگر لایه جدید دقیقاً روی صفحه A قرار گیرد، این باعث به وجود آمدن سری زیر میشود:
...ABABAB...
این آرایش اتمی در ساختار کریستالی HCP مشاهده می شود.اما اگر این سه لایه نسبت به یکدیگر متفاوت باشند تا لایه چهارم دقیقاً روی لایه A قرار گیرد و سری تکرار شود، سری زیر حاصل میشود:
...ABCABCABC...
این نوع از قرار گرفتن اتمها در ساختار FCC قابل مشاهده است.
ساختار تتراگونال (Tetragonal)
در این ساختار پارامتر های شبکه a و b با یکدیگر برابر اما پارامتر c متفاوت می باشد و تمام زوایا نیز برابر 90 درجه است.این ساختار دو نوع ساده(Simple) و مرکزپر(Body centered) دارد و از جمله موادی که دارای این ساختار هستند می توان به ولفنیت ، کاسیتریت و کالکوپیریت اشاره کرد.
ساختار ارتورومبیک (Orthorhombic)
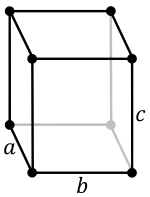

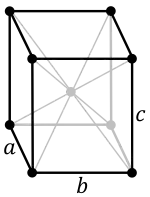
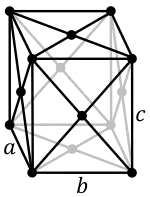
در این ساختار پارامتر های شبکه a,bوc با یکدیگر متفاوت اما تمام زوایا برابر 90 درجه است. این ساختار انواع ساده(Simple)،مرکز پر(Body centered)،وجوه مرکزپر(Face centered) و وجوه قاعده مرکزپر(Base centered) را شامل می شود.کانی های توپاز،انستاتیت و گوگرد دارای اینگونه ساختار می باشند.
ساختار رمبوهدرال (Rhombohedral)
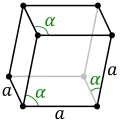
در این ساختار تمام پارامتر های شبکه با هم برابر می باشند یعنی اضلاع شبکه با یکدیگر برابر و زوایا نیز برابرند اما 90 درجه نیستد ولی کمتر از 120 درجه می باشند. این ساختار تنها نوع ساده(Simple) را شامل می شود و کانی هایی همچون دولومیت و هماتیت این ساختار را دارند.
ساختار منوکلینیک (Monoclinic)
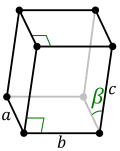
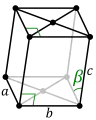
در این ساختار پارامترهای شبکه a,bوc باهم برابر نیستند اما از طرفی زوایای α و γ باهم برابر و 90 درجه است و زاویه β مقداری متفاوت دارد.این ساختار دو نوع ساده(simple) و پایه مرکزپر(Base centered) را شامل می شود و کانی هایی همچون ارتوکلاز و ژیپس دارای این ساختار می باشند.
ساختار تریکلینیک (Triclinic)
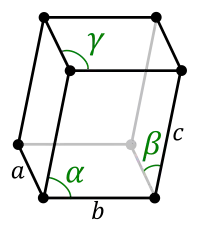
در این ساختار هیچ یک از پارامترهای شبکه با یکدیگر برابر نیست و تمام اضلاع و زوایای شبکه واحد با یکدیگر متفاوت است.این ساختار تنها نوع ساده(simple) را شامل می شود و کانی هایی همچون میکروکلین و کائولینیت دارای این ساختار می باشند.
حجم انواع ساختارهای کریستالی در جدول زیر آمده است:
| دستگاه بلوری | حجم | |||
| سهشیب (تریکلینیک) | ||||
| تکشیب (منوکلینیک) | ||||
| راستلوزی (ارترومبیک) | ||||
| چهارگوشه (تتراگونال) | ||||
| لوزیپهلو (رمبوهدرال) | ||||
| ششگوشه (هگزاگونال) | ||||
| مکعبی | ||||
چهاربعد
در چهار بعد ۵۲ شبکه براوه را میتوان تصور کرد.
جستارهای وابسته
منابع
- GREGORY S. ROHRER, Structure and Bonding in Crystalline Materials, Cambridge University Press, 2004.
- Silberberg, Martin S, Chemistry: the molecular nature of matter and change with advanced topics, Mc Graw Hill Education,2018
- After W.G. Moffatt, G.W. Pearsall, & J. Wulff, The Structure and Properties of Materials vol. I: “Structure,” Wiley, 1964,
- Hurlbut, Cornelius S. ; Klein, Cornelis, 1985, Manual of Mineralogy, 20th ed. , pp. 64 - 65, ISBN 0-471-80580-7
- https://www.nde-ed.org/EducationResources/CommunityCollege/Materials/Structure/metallic_structures.htm
- https://www.e-education.psu.edu/matse81/node/2134
- Wiliam D. Callister, Jr. David G. Rethwisch,Material science and engineering: an introduction,Wiley,2018
- http://www.packmangroup.com/content/1250/%DA%A9%D8%B1%DB%8C%D8%B3%D8%AA%D8%A7%D9%84%D9%88%DA%AF%D8%B1%D8%A7%D9%81%DB%8C
- http://edu.nano.ir/paper/806
- تویسرکانی،حسین،اصول علم مواد(ساختار،خواص و مهندسی مواد)،دانشگاه صنعتی اصفهان،اصفهان،1393