جذب لانداو

به دلیل تبادل انرژی بین یک موج الکترومغناطیسی با سرعت فیزیکی ${\displaystyle v_{\text{ph}}}$ و ذرات در پلاسما با سرعت تقریباً برابر با ${\displaystyle v_{\text{ph}}}$، که می‌تواند به شدت با موج در تعامل باشد، جذب لانداو رخ می‌دهد.[8] این ذرات با سرعت اندکی کمتر از ${\displaystyle v_{\text{ph}}}$ برای حرکت با سرعت فاز موج از میدان الکتریکی موج شتاب می‌گیرند، در حالی که ذرات با سرعت اندکی بزرگتر از ${\displaystyle v_{\text{ph}}}$ شتاب منفی می‌گیرند و انرژی خود را به موج منتقل می‌کنند: ذرات تمایل دارند با موج همگام شوند. این موضوع به صورت آزمایشی با یک لامپ مایکروویو انجام شده‌است.[9]

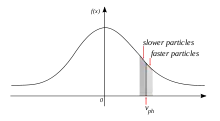
در یک پلاسما MHD ایده‌آل، سرعت ذرات تقریباً یک تابع توزیع ماکسولی دارد. اگر شیب تابع منفی باشد، تعداد ذرات با سرعت کمی کمتر از سرعت فاز موج بیشتر از تعداد ذرات با سرعت کمی بیشتر از سرعت فاز موج، است. از این رو، ذرات بیشتری از موج انرژی می‌گیرند تا ذراتی که به موج انرژی می‌دهند، که منجر به جذب موج می‌شود. اگر، با این حال، شیب تابع مثبت باشد، تعداد ذرات با سرعت کمی کمتر از سرعت فاز موج، کمتر از تعداد ذرات با سرعت کمی بیشتر از سرعت فاز موج است. از این رو، ذرات بیشتری به موج انرژی می‌دهند تا آنهایی که انرژی می‌گیرند، که منجر به افزایش انرژی موج می‌شود.

تئوری ریاضی جذب لانداو تا حدودی گفته شده‌است - بخش زیر را ببینید. با این حال، یک تفسیر فیزیکی ساده وجود دارد [در بخش 7.5 [2]با یک پیش نویس معرفی شده‌است] که، اگر چه به‌طور کامل درست نیست، اما به تصویر کشیدن این پدیده کمک می‌کند.

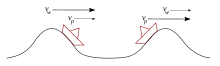
امواج لانگمویور به عنوان امواج در دریا می‌توان تصور کرد و ذرات به عنوان موج سوارانی تلاش می‌کنند که موج را بگیرند و همه در همان مسیر حرکت می‌کنند. اگر موج سوار در سطح آب با سرعت کمی کمتر از امواج حرکت کند، سرانجام در امتداد موج، (در حال به دست آوردن انرژی) موج از آن عبور می‌کند و در حالی که یک موج سواری کمی سریعتر از موج حرکت می‌کند موج را درحالی که بالای آن است، هول می‌دهد (از دست دادن انرژی به موج).

شایان ذکر است که فقط موج سواران نقش مهمی در این تعاملات انرژی با امواج بازی می‌کنند؛ وقتی یک موج از یک توپ ساحلی شناور بر روی آب (سرعت صفر) گذر می‌کند، این توپ به سمت بالا و پایین می‌رود، و هیچ انرژی را دریافت نمی‌کند. همچنین، یک قایق که بسیار سریع حرکت می‌کند (سریعتر از امواج) با موج انرژی زیادی مبادله نمی‌کند.

شرح ساده مکانیکی از دینامیک ذرات یک برآورد کمی از هماهنگ سازی ذرات با موج [معادله (۱) از[9]] فراهم می‌کند. یک روش دقیق تر نشان می‌دهد که برای ذرات با سرعت در حدود موج، متناسب با میزان میرایی و مستقل از دامنه موج، یک هماهنگی قوی رخ می‌دهد[بخش ۴٫۱٫۳ از[10]]. از آنجائیکه میرایی لانداو برای امواج با دامنه دلخواه کوچک به وجود می‌آید، این نشان می‌دهد که فعال‌ترین ذرات در این میرایی از به دام افتادن بسیار دور هستند. این طبیعی است، زیرا به دام افتادن در مقیاس زمانی کاهشی برای موجی مثل (به‌طور خاص ${\displaystyle T_{\text{trap}}\sim A^{-1/2}}$ برای دامنه موج ${\displaystyle A}$) رخ می‌دهد.

توجیه نظری با معادله ولاسکو در با فرض صفر بودن میدان مغناطیسی و غیر نسبیتی بودن، آغاز می‌شود؛ مجموعه معادلات Vlasov-Poisson. راه حل‌های صریح در حد یک میدان کوچک به دست می‌آید. تابع توزیع ${\displaystyle f}$و میدان ${\displaystyle E}$در یک سری گسترش می‌یابد:

${\displaystyle f=f_{0}(v)+f_{1}(x,v,t)+f_{2}(x,v,t)}$ ، ${\displaystyle E=E_{1}(x,t)+E_{2}(x,t)}$ ترم‌های هم مرتبه جمع‌آوری شده‌است.

معادلات مرتبه اول Vlasov-Poisson را بخوانید: ${\displaystyle (\partial _{t}+v\partial _{x})f_{1}+{e \over m}E_{1}f'_{0}=0,\quad \partial _{x}E_{1}={e \over \epsilon _{0}}\int f_{1}\mathrm {d} v}$

لانداو موجی ناشی از اختلال اولیه ${\displaystyle f_{1}(x,v,0)=g(v)\exp(ikx)}$[1] و با کمک تبدیل لاپلاس و انتگرال‌گیری روی مسیر یک موج حرکتی میرا ${\displaystyle \exp[ik(x-v_{\text{ph}}t)-\gamma t]}$ با عدد موج ${\displaystyle k}$و میزان کاهش میرایی ${\displaystyle \gamma \approx -{\pi \omega _{p}^{3} \over 2k^{2}N}f'_{0}(v_{\text{ph}}),\quad N=\int f_{0}\mathrm {d} v}$ را محاسبه کرد.

در اینجا ${\displaystyle \omega _{p}}$فرکانس نوسان پلاسما و ${\displaystyle N}$چگالی الکترون است. بعدها نیکو ون کپن ثابت کرد که همان نتیجه را می‌توان با تبدیل فوریه بدست آورد.[11] او نشان داد که معادلات Vlasov-Poisson خطی شده دارای یک طیف پیوسته از مدهای تکین طبیعی است که در حال حاضر به عنوان مدهای ون کپن شناخته می‌شود. ${\displaystyle {\frac {\omega _{p}^{2}}{kN}}f'_{0}{\frac {\mathcal {P}}{kv-\omega }}+\epsilon \delta \left(v-{\frac {\omega }{k}}\right)}$ که در آن ${\displaystyle {\mathcal {P}}}$ارزش اصلی را نشان می‌دهد، ${\displaystyle \delta }$تابع دلتا (مشاهده تابع تعمیم یافته) است و ${\displaystyle \epsilon =1+{\frac {\omega _{p}^{2}}{kN}}\int f'_{0}{\frac {\mathcal {P}}{\omega -kv}}\mathrm {d} v}$ گذردهی پلاسما است. او با تجزیهٔ اختلال اولیه دراین مدها طیف فوریه موج بوجود آمده را به دست آورد. جذب، توسط ترکیب فاز این مدهای فوریه با اختلاف فرکانس‌های کم در نزدیکی ${\displaystyle \omega _{p}}$توضیح داده شده‌است. معلوم نیست که چگونه میرایی می‌تواند در یک پلاسما غیربرخوردی رخ دهد: انرژی موج کجا می‌رود؟ در نظریه سیالی، که در آن پلاسما به عنوان یک ماده دی الکتریک پراکنده مدل‌سازی شده‌است،[12] انرژی امواج لانگمویر اینگونه است: انرژی میدان ضربدر فاکتور بریلوئین ${\displaystyle \partial _{\omega }(\omega \epsilon )}$. اما جذب در این مدل نمی‌تواند مقداردهی شود. برای محاسبه تبادل انرژی موج با الکترون‌های نوسانی، تئوری پلاسما ولاسوو باید به درجه دوم گسترش یابد و مشکلات مربوط به شرایط اولیه مناسب و شرایط عمومی رخ می‌دهد.

در مرجع.[13] این مشکلات مورد مطالعه قرار گرفته‌است. از آنجا که محاسبات برای موج بی‌نهایت در مرتبه دوم کارامد نیستند، یک بسته موج تجزیه و تحلیل می‌شود. شرایط اولیه درجه دوم پیدا شده‌است که رفتار عمومی را متوقف می‌کند و یک بسته موج را که انرژی آن با تئوری سیالی موافق است، تحریک می‌کند. این شکل چگالی انرژی یک بسته موج را که در سرعت گروهی حرکت می‌کند نشان می‌دهد، انرژی آن توسط الکترون‌هایی که در سرعت فاز حرکت می‌کنند، حمل می‌شود. مجموع انرژی، ناحیه زیر منحنی، حفظ می‌شود.

تئوری دقیق ریاضی مبتنی بر حل مسئله کوشی برای معادله تکاملی (در اینجا معادله دیفرانسیل جزئی ولاسوو-پواسن) و اثبات برآوردها در راه حل است.

ابتدا تئوری ریاضی خطی شده و کامل توسعه یافته‌است.[14]

فراتر از معادله خطی شده رفتن و مقابله با غیر خطی بودن، یک مشکل قدیمی در نظریه ریاضی جذب (میرایی) لانداو است. پیش از این، یک نتیجه ریاضی در سطح غیر خطی، وجود یک دسته از مقادیر میرایی نمایی از حل معادله ولاسوو-پواسن در یک چرخه بود[15] که با استفاده از تکنیک پراکندگی اثبات شده بود (این نتیجه اخیراً گسترش یافته‌است).[16] با این حال وجود این نتایج هیچ چیز راجع به اینکه چه داده‌های اولیه ای می‌تواند به چنین راه حل‌هایی برای میرایی منجر نمی‌شود، نشان نمی‌دهد.

در یک مقاله متاخر،[17] مسئله داده اولیه حل شده‌است و میرایی لانداو برای اولین بار برای معادله ولاسکو غیر خطی ساخته شده‌است. ثابت شده‌است که راه حل‌هایی که در مجاورت (برای توپولوژی تحلیلی یا جوی) یک راه حل موضعی همگن خطی ثابت (به صورت اوربیتال) شروع شده‌است، برای همه زمان‌ها پایداراند و در طول زمان بطورکلی جذب می‌شوند. پدیدهٔ جذب در ترم‌های انتقال ترتیب ${\displaystyle f}$ به عنوان یک تابع از ${\displaystyle x}$ و ${\displaystyle v}$به جای مبادلات انرژی، تعریف می‌شود. تغییرات در مقیاس بزرگ از تغییرات در مقیاس کوچکتر گذر می‌کند و مقیاس کوچکتر در فضای سرعت، مطابق با تغییر طیف فوریه ${\displaystyle f}$به عنوان تابعی از ${\displaystyle v}$است. این تغییر، به خوبی در نظریه خطی شناخته شده‌است، ثابت می‌کند که در مورد غیر خطی هم حفظ شده‌است.

یک عبارت برای گذردهی پلاسما مشابه یکی از موارد فوق، اما مطابق با تبدیل لاپلاس است که توسط لانداو استفاده شد، می‌تواند به سادگی در یک چارچوب N-body بدست آید. یک پلاسما (یک جزئی) را در نظر می‌گیریم که در آن فقط الکترون‌ها به عنوان ذرات حضور دارند و یون‌ها فقط یک پس زمینه خنثی کننده را ارائه می‌دهند. قاعده محاسبه با در نظر گرفتن حرکت خطی خیالی یک ذره در یک مولفه فوریه از میدان الکتریکی خودش، ارائه شده‌است. محاسبه کامل با جمع نتیجه مربوطه بر روی همه N ذره و همه مولفه‌های فوریه، حاصل می‌شود. بیان ولاسووی برای گذردهی پلاسما در نهایت با جایگزینی یک انتگرال بر روی یک تابع توزیع ملایم برای مجموع گسسته بر روی ذرات در گذردهی پلاسمای N ذره ای، بهبود یافت. این روش مکانیکی همراه با جذب لانداو، یک محاسبه برای محافظ دیبای یا غربالگری میدان الکتریکی را در یک پلاسما فراهم می‌کند.

• List of plasma (physics) articles