آشکارساز لبه کنی

تصویر پس از عبور ماسک ۵×۵ گوسی روی هر پیکسل.

از آنجائیکه همه نتایج آشکارسازی لبه به سادگی تحت تأثیر نویز در تصویر قرار می‌گیرند، برای جلوگیری از آشکارسازی غلط ناشی از نویز، فیلتر کردن نویزها ضروری است. برای هموار کردن تصویر، یک کرنل گوسی با تصویر پیچش داده می‌شود. این مرحله تصویر را اندکی هموار می‌کند تا آثار نویزهای واضح روی آشکارساز لبه کاهش یابد. معادله کرنل یک فیلتر گوسی به اندازه (2k+۱)×(2k+۱) در زیر آورده شده‌است.

${\displaystyle H_{ij}={\frac {1}{2\pi \sigma ^{2}}}\exp \left(-{\frac {(i-(k+1))^{2}+(j-(k+1))^{2}}{2\sigma ^{2}}}\right);1\leq i,j\leq (2k+1)}$

این مثالی از یک فیلتر گوسی ۵×۵، که برای ایجاد تصویر مقابل استفاده شده‌است، با ۱٫۴ = ${\displaystyle \sigma }$ می‌باشد. (ستاره عملگر پیچش را نشان می‌دهد).

${\textstyle \mathbf {B} ={\frac {1}{159}}{\begin{bmatrix}2&4&5&4&2\\4&9&12&9&4\\5&12&15&12&5\\4&9&12&9&4\\2&4&5&4&2\end{bmatrix}}*\mathbf {A} .}$

درک این امر که انتخاب اندازه کرنل گوسی روی عملکرد آشکارساز اثر می‌گذارد مهم است. هر چه اندازه بیشتر باشد، آشکارساز حساسیت کمتری نسبت به نویز دارد. به علاوه خطای محلی سازی برای آشکارکردن لبه با افزایش اندازه کرنل فیلتر گوسی اندکی افزایش پیدا می‌کند. اندازه ۵×۵ در بیشتر موارد مناسب است اما می‌تواند بسته به شرایط خاص متفاوت باشد.

لبه یک تصویر ممکن است در راستاهای مختلفی باشد، در نتیجه الگوریتم Canny از 4 فیلتر برای تشخیص لبه‌های افقی، عمودی و قطری در تصویر هموار شده استفاده می‌کند. عملگر لبه یاب (برای مثال Roberts, Prewitt یا Sobel)، مشتق اول در راستای افقی (Gx) و عمودی (Gy) بدست می‌دهد. با استفاده از آن‌ها می‌توان گرادیان و راستای لبه را مشخص کرد:

${\textstyle \mathbf {G} ={\sqrt {{\mathbf {G} _{x}}^{2}+{\mathbf {G} _{y}}^{2}}}}$

${\textstyle \mathbf {\Theta } =\operatorname {atan2} \left(\mathbf {G} _{y},\mathbf {G} _{x}\right)}$

که G با استفاده از تابع hypot و atan2 که تابع عکس تانژات با دو آرگومان است حساب می‌شود. جهت لبه به ۴ راستای عمودی، افقی و قطری (۲ راستا) رند می‌شود (°۰، °۴۵، °۹۰ و °۱۳۵). زاویه مشخصی به جهت لبه در هر ناحیه رنگی نسبت داده می‌شود برای مثال برای θ در بازه [°۰, °۲۲٫۵] یا [°۱۵۷٫۵,°۱۸۰] به °۰ نگاشت می‌شود.

سرکوب غیر بیشینه یک روش نازک کننده لبه است.

سرکوب نقاط غیر بیشینه یک روش برای نازک کردن لبه است. سرکوب نقاط غیر بیشینه برای یافتن «بزرگترین لبه» استفاده می‌شود. پس از اعمال محاسبات گرادیان، لبه بدست آمده از مقدار گرادیان همچنان به‌طور کامل تار است. با توجه به معیار ۳، تنها باید یک پاسخ دقیق به لبه وجود داشته باشد. به این ترتیب سرکوب نقاط غیر بیشینه می‌تواند به سرکوب همه مقادیر گرادیان (با صفر کردن آن‌ها) به جز بیشینه‌های محلی که نشان دهنده مکان‌هایی با سریعترین تغییر در مقدار روشنایی هستند کمک کند. این الگوریتم برای هر پیکسل در تصویر گرادیان به شرح زیر است:

1. مقایسه قدرت لبه پیکسل کنونی با قدرت لبه پیکسل در راستاهای مثبت و منفی گرادیان.
2. اگر قدرت لبه پیکسل کنونی در مقایسه با دیگر پیکسل‌ها که در یک راستا (برای مثال یک پیکسل که جهت آن در راستای y است با پیکسل‌های بالا و پایین در محور عمودی مقایسه می‌شود) هستند بزرگترین باشد، مقدار نگه داشته می‌شود. در غیر اینصورت مقدار سرکوب می‌شود

در برخی از پیاده‌سازی‌ها، الگوریتم جهت‌های پیوسته گرادیان را به مجموعه ای از جهت‌های گسسته دسته‌بندی می‌کند، و بعد یک فیلتر 3x3 را روی خروجی مرحله قبل (که قدرت لبه و جهت گرادیان است) حرکت می‌دهد. در هر پیکسل، این الگوریتم قدرت لبه پیکسل مرکزی را سرکوب می‌کند (با صفر کردن مقدار آن) اگر اندازه آن بزرگتر از اندازه دو همسایه آن در راستای گرادیان نباشد. برای مثال،

• اگر زاویه رند شده گرادیان صفر (یعنی لبه در راستای جنوبی-شمالی باشد) و اندازه گرادیان بزرگتر از اندازه پیکسل‌ها در جهت‌های شرق و غرب باشد به عنوان نقطه روی لبه در نظر گرفته می‌شود.
• اگر زاویه رند شده گرادیان °۹۰ (یعنی لبه در راستای شرقی-غربی باشد) و اندازه گرادیان بزرگتر از اندازه پیکسل‌ها در جهت‌های شمال و جنوب باشد به عنوان نقطه روی لبه در نظر گرفته می‌شود.
• اگر زاویه رند شده گرادیان °۱۳۵ (یعنی لبه در راستای شمال شرقی-جنوب غربی باشد) و اندازه گرادیان بزرگتر از اندازه پیکسل‌ها در جهت‌های شمال غرب و جنوب شرق باشد به عنوان نقطه روی لبه در نظر گرفته می‌شود.
• اگر زاویه رند شده گرادیان °۴۵ (یعنی لبه در راستای شمال غربی-جنوب شرقی باشد) و اندازه گرادیان بزرگتر از اندازه پیکسل‌ها در جهت‌های شمال شرق و جنوب غرب باشد به عنوان نقطه روی لبه در نظر گرفته می‌شود.

در پیاده‌سازی‌های دقیقتر، از درون یابی خطی بین دو پیکسل همسایه که بین مسیر گرادیان قرار دارند استفاده می‌شود. برای مثال اگر زاویه گرادیان بین °۸۹ و °۱۸۰ باشد، درون یابی بین گرادیان‌ها در پیکسل‌های شمال و شمال شرق یک مقدار درون یابی شده و درون یابی بین پیکسل‌های جنوب و جنوب غرب یک مقدار دیگر بدست می‌دهد (با استفاده از قواعد پاراگراف آخر). اندازه گرادیان در پیکسل مرکزی باید بزرگتر از هر دو پیکسل که به عنوان لبه در نظر گرفته شده‌اند باشد.

دقت شود که علامت جهت اهمیتی ندارد، یعنی شمال-جنوب با جنوب-شمال و یه همین ترتیب برابر است.

پس از اعمال سرکوب غیر بیشینه، پیکسل‌های لبه باقی مانده، ارائه دقیقتری از لبه‌های واقعی تصویر دارند. اگرچه بعضی از پیکسل لبه‌ها به علت نویز و تغییرات رنگ باقی می‌مانند. برای در نظر گرفتن این پاسخ‌های غیر واقعی، فیلتر کردن پیکسل‌های لبه با مقدار گرادیان ضعیف و نگه داشتن پیکسل‌های لبه با مقدار گرادیان زیاد ضروری است. این کار با انتخاب آستانه کم و زیاد صورت می‌گیرد. اگر گرادیان یک پیکسل لبه بزرگتر از آستانه زیاد باشد پیکسل لبه قوی حساب می‌شود. اگر گرادیان یک پیکسل لبه کوچکتر از آستانه زیاد و بزرگتر از آستانه کم باشد پیکسل لبه ضعیف حساب می‌شود. این دو آستانه به صورت تجربی تعیین می‌شوند و تعریف آن‌ها بستگی به محتوای تصویر ورودی داده شده دارد.

لبه یابی Canny اعمال شده به یک تصویر.

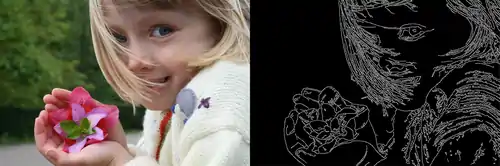
تا اینجا پیکسل‌های لبه قوی قطعاً باید در تصویر لبه نهایی جای بگیرند، زیرا آن‌ها از لبه‌های واقعی در تصویر بدست آمده‌اند. اگر چه بحث‌هایی در مورد پیکسل‌های لبه ضعیف وجود دارد، زیرا این پیکسل‌ها می‌تواند هم از لبه واقعی و هم از تغییرات رنگ/نویز بدست آیند. برای رسیدن به نتیجه دقیق، لبه‌های ضعیف ناشی از تغییرات رنگ یا نویز باید حذف شوند. معمولاً یک پیکسل لبه ضعیف که ناشی از لبه‌های واقعی هستند به پیکسل لبه قوی متصل است در صورتی که پاسخ‌های نویز متصل نیستند. برای دنبال کردن اتصال لبه، آنالیز blob به وسیله نگاه کردن به پیکسل لبه قوی و پیکسل‌های همسایگی ۸-اتصاله اعمال می‌شود. از آنجائیکه تنها یک پیکسل لبه قوی در blob نقش دارد، آن نقطه لبه ضعیف می‌تواند به عنوان نقطه ای که باید حفظ شود تشخیص داده شود.

از آنجائیکه لبه و نویز به عنوان سیگنال فرکانس بالا شناسایی می‌شوند، فیلتر گوسی ساده هر دو را هموار می‌کند. اگرچه برای رسیدن به تشخیص لبه واقعی با دقت بالا انتظار می‌رود که همواری بیشتر باید به نویز و همواری کمتر باید به لبه اعمال شود. Bing Wang و Shaosheng Fan از Changsha University of Science and Technology یک فیلتر وفقی توسعه دادند که ناپیوستگی بین مقادیر greyscale در هر پیکسل را ارزیابی می‌کند. هرچه ناپیوستگی بیشتر باشد، مقدار وزن کمتری برای فیلتر هموارکننده در آن نقطه در نظر گرفته می‌شود. متقابلاً هر چه ناپیوستگی بین مقادیر greyscale کمتر باشد، مقدار وزن بیشتری برای فیلتر در نظر گرفته می‌شود. فرایند پیاده‌سازی این فیلتر وفقی در ۵ مرحله می‌تواند خلاصه شود:

1. k = ۱، تعداد تکرار n وضریب اندازه لبه h در نظر گرفته می‌شود.
2. مقادیر گرادیان ${\displaystyle G_{x}(x,y)}$ و ${\displaystyle G_{y}(x,y)}$ محاسبه شود.
3. وزن بر اساس فرمول زیر محاسبه شود.

${\textstyle d(x,y)={\sqrt {G_{x}(x,y)^{2}+G_{y}(x,y)^{2}}}}$

${\textstyle w(x,y)=\exp \left(-{\frac {\sqrt {d(x,y)}}{2h^{2}}}\right)}$

۴. رابطه فیلتر برای هموار کردن تصویر برابر است با:

${\textstyle f(x,y)={\frac {1}{N}}\sum \limits _{i=-1}^{1}\sum \limits _{j=-1}^{1}f(x+i,y+j)w(x+i,y+j)}$

برای هموار کردن تصویر که

${\textstyle N=\sum \limits _{i=-1}^{1}\sum \limits _{j=-1}^{1}w(x+i,y+j)}$

۵. زمانی که k = n تکرار را متوقف کن در غیر اینصورت k = k+1، و به مرحله ۲ بازگرد.

اندازه و جهت گرادیان می‌تواند از طریق عملگرهای لبه یابی متفاوتی محاسبه شود و انتخاب عملگر بر کیفیت نتایج اثر می‌گذارد. به‌طور رایج فیلتر 3x3 Sobel انتخاب می‌شود. اگر چه فیلترهای دیگر ممکن است بهتر باشد از جمله فیلتر 5x5 Sobel که نویز را کاهش می‌دهد یا فیلتر Scharr که تقارن چرخشی بهتری دارد. انتخاب‌های رایج دیگر Prewitt (استفاده شده توسط Zhou) و Roberts Cross هستند.

برای برطرف کردن چالش‌هایی که در آن تشخیص آستانه دوگانه به صورت تجربی دشوار است، روش Otsu می‌تواند بر تصویر اندازه گرادیان که سرکوب غیر بیشینه شده‌است برای ایجاد آستانه زیاد اعمال شود. آستانه کم معمولاً نصف آستانه زیاد در این حالت تنظیم می‌شود. از آنجائیکه تصویر اندازه گرادیان مقادیر پیوسته بدون بیشینه مشخص دارد، روش Otsu باید برای استفاده از جفت‌های مقدار/تعداد به جای کل هیستگرام وفق داده شود.

با اینکه لبه یابی قدیمی Canny خروجی تشخیص خوبی را با در نظرگرفتن دو معیار اول بدست می‌دهد، اما پاسخ منفرد برای هر لبه را به‌طور دقیق برآورده نمی‌کند. ریخت‌شناسی ریاضی برای باریک کردن لبه شناسایی شده توسط Mallat S و Zhong توسعه داده شد.

به جای فیلتر گوسی و تخمین گرادیان از Curvelets برای محاسبه میدان برداری که جهت‌ها و اندازه‌های آن جهت و قدرت لبه‌ها در تصویر را تقریب می‌زند استفاده شده‌است که در مراحل ۳ تا ۵ الگوریتم Canny اعمال می‌شود. Curvelets سیگنال‌ها را به مولفه‌های جداگانه مقیاس‌های متفاوت تجزیه می‌کند و کاهش مؤلفه‌های مقیاس‌های نرمتر می‌تواند نویز را کاهش دهد.