پروتکل تبادل کلید دیفی-هلمن

تا قبل از انتشار این پروتکل، رمزنگاری بیشتر به صورت رمزنگاری کلید متقارن مورد استفاده قرار می‌گرفته‌است. در سال ۱۹۷۶، با انتشار این پروتکل، پایهٔ اولیهٔ رمزنگاری کلید نامتقارن بنا شد که بعداً با فعالیت‌های رالف مرکل تکمیل گردید. مدتی بعد نیز الگوریتم رمز مشهور آراس‌ای که از مبانی مشابهی برخوردار است مطرح گردید.

در سال ۱۹۹۷، یک مؤسسه تحقیقاتی جاسوسی در انگلستان ادعا کرد که پروتکل دیفی-هِلمن، قبل از سال ۱۹۷۶ توسط فردی به نام مالکولم ویلیامسون در آن مؤسسه اختراع شده و تنها به دلایل امنیتی از انتشار آن جلوگیری شده بوده‌است.

در سال ۲۰۰۲، مارتین هِلمن در کتابش خاطرنشان کرد که رالف مِرکل نیز به همان اندازهٔ دیفی و هِلمن در ایجاد و گسترش رمزنگاری کلید نامتقارن تأثیرگذار بوده‌است و پیشنهاد کرد که این پروتکل به نام دیفی-هِلمن-مِرکل شناخته شود.

در سال‌های بعد از ۱۹۷۶ و با گسترش تدریجی رمزنگاری کلید نامتقارن، پروتکل‌های تبادل کلید مختلفی با استفاده از پروتکل دیفی-هلمن و با قابلیت‌های بیشتری نسبت به آن طراحی شده‌است.

در فرمول‌های پیشنهادی اولیه این پروتکل، از گروه همنهشتی اعداد صحیح با پیمانهٔ عدد اول p و عملگر ضرب اعداد صحیح استفاده شده‌است. در این گروه عددی، یک ریشهٔ اولیه محاسبه می‌شود که آن را با g نشان می‌دهند.

ایجاد و تبادل کلید رمز با پروتکل دیفی-هلمن

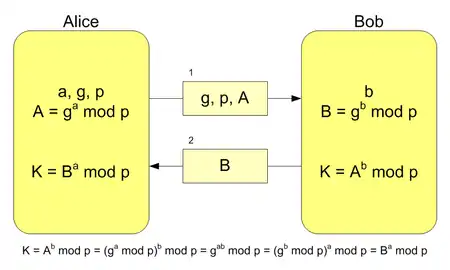
سپس مراحل زیر که در شکل روبرو هم نشان داده شده‌است، انجام می‌شود:

1. مقدار عدد اول دلخواه بزرگ p (پیمانهٔ عمل ضرب) و مقدار محاسبه شده برای g میان دو طرف رد و بدل می‌شود.
2. هر یک از دو طرف یک عدد صحیح دلخواه (a و b) را به صورت پنهانی در نظر می‌گیرد.
3. هر یک از دو طرف با استفاده از عمل به توان رسانی پیمانه ای و مقادیر قبلی (p و g و مقدار پنهانی)، یک مقدار جدید محاسبه کرده (A و B) و برای طرف مقابل ارسال می‌کند.
4. طرف اول با استفاده از مقادیر p و g و a و B، و طرف دوم با استفاده از مقادیر p و g و b و A، و با همان عمل توان پیمانه‌ای مقدار جدیدی را محاسبه می‌کنند. مقدار جدید محاسبه شده -چنان‌که فرمول نشان می‌دهد- در دو طرف یکسان و همان کلید رمز مشترک است.

توجه به دو نکته دربارهٔ این پروتکل لازم است:

• مقادیر a و b و مقدار مشترک محاسبه شده، هرگز مستقیماً از کانال ارتباطی عبور نمی‌کنند. بقیهٔ مقادیر یعنی p و g و A و B از کانال ارتباطی عبور می‌کنند و برای دیگران قابل دسترسی هستند.
• دشواری حل مسئلهٔ لگاریتم گسسته تضمین می‌کند که مقادیر a و b و مقدار کلید رمز مشترک، با داشتن مقدار اعداد دیگر در عمل قابل محاسبه نباشد.

طرف اول پنهان محاسبه ارسال p, g a ga mod p … gb mod p)a mod p)

${\displaystyle \leftarrow }$ ${\displaystyle \rightarrow }$ =

طرف دوم ارسال محاسبه پنهان p, g b … gb mod p ga mod p)b mod p)

در اینجا برای سهولت در فهم مطلب یک مثال عددی از ایجاد و تبادل کلید با پروتکل دیفی-هلمن ارائه شده‌است. در عمل، اعدادی که مورد استفاده قرار می‌گیرند بسیار بزرگ هستند که ممکن است بیش از صد رقم داشته باشند.

1. دو طرف روی مقدار عدد اول ۲۳ = p و مقدار اولیهٔ ۵ = g توافق می‌کنند.
2. طرف اول مقدار پنهانی ۶ = a را انتخاب و (g^a mod p) را برای طرف دوم ارسال می‌کند.
   • ۸ = (۲۳ ۵^۶mod)
3. طرف دوم مقدار پنهانی ۱۵ = b را انتخاب و (g^b mod p) را برای طرف اول ارسال می‌کند.
   • ۱۹ = (۲۳ ۵^۱۵mod)
4. طرف اول مقدار g^b mod p)^a mod p) را محاسبه کرده و به عنوان کلید رمز مشترک در نظر می‌گیرد.
   • ۲ = (۲۳ ۱۹^۶mod)
5. طرف دوم مقدار g^a mod p)^b mod p) را محاسبه کرده و به عنوان کلید رمز مشترک در نظر می‌گیرد.
   • ۲ = (۲۳ ۸^۱۵mod)

امنیت این پروتکل مبتنی بر دشواری حل مسئلهٔ لگاریتم گسسته است.

در حال حاضر مسائل زیر باید در ارتباط با امنیت پروتکل دیفی-هلمن لحاظ گردد:

• بر اساس قدرت محاسباتی رایانه‌های امروزی، استفاده از عدد اول p با حدود ۳۰۰ رقم و اعداد a و b با حدود ۱۰۰ رقم می‌تواند شکستن امنیت این پروتکل و یافتن کلید رمز مشترک را در عمل غیرممکن سازد.
• در عمل هر عدد اول بزرگی را نمی‌توان در این پروتکل به کار گرفت، بلکه لازم است عدد p مورد استفاده یک عدد اول امن باشد. در غیر این صورت شکستن امنیت این پروتکل و یافتن کلید رمز مشترک، با استفاده از الگوریتم‌هایی مانند الگوریتم پولیگ-هلمن، نسبتاً آسان و در زمان کمتری قابل انجام خواهد شد.
• اعداد پنهانی a و b باید به صورت عدد تصادفی تولید شوند و مولد عدد تصادفی مورد استفاده هم نباید تکرارپذیر و قابل پیش‌بینی باشد. در غیر این صورت، یافتن کلید رمز مشترک آسان‌تر و در زمان کمتری قابل انجام خواهد شد.

فرمول‌های پیشنهادی اولیه این پروتکل که در قسمت بالا ارائه شد، امکان شناسایی متقابل دو طرف را فراهم نمی‌سازد. به همین دلیل اگر طرف سومی روی خط ارتباطی و بین طرف اول و دوم قرار بگیرد، می‌تواند بدون اینکه شناسایی شود، با هر یک از دو طرف به‌طور جداگانه طبق پروتکل دیفی-هلمن به رد و بدل کلید رمز بپردازد. (به چنین نوع حمله‌ای، حمله مرد میانی گفته می‌شود). به این ترتیب طرف سوم خواهد توانست بدون اینکه طرف‌های اول و دوم متوجه شوند، تمام پیام‌های آن دو را بخواند که برای این کار کافی است ابتدا پیام هر یک از آن‌ها را با کلید رمز مربوط به خودش رمزگشایی کند و سپس با کلید رمز طرف دیگر رمزگذاری کرده و برایش ارسال کند.

برای مقاوم کردن پروتکل دیفی-هلمن در مقابل این مشکل، لازم است که یک مکانیزم برای شناسایی دو طرف به مراحل این پروتکل اضافه شود. همین امر باعث شده‌است که پروتکل‌های مختلف شناسایی با استفاده از مکانیزم تبادل کلید دیفی-هلمن ارائه شود.

• رمزشناس
• ویتفیلد دیفی
• مارتین هلمن
• رمزنگاری کلید نامتقارن
• آراس‌ای
• لگاریتم گسسته
• توان پیمانه‌ای

• ویکی‌پدیای انگلیسی

• نگاهی به Diffie–Hellman Key Exchange