هماهنگ‌های کروی

هماهنگ‌های کروی حقیقی، Y_lm، برای l=0 تا l=4 (بالا به پایین) و m=0 تا m=4 (چپ به راست).

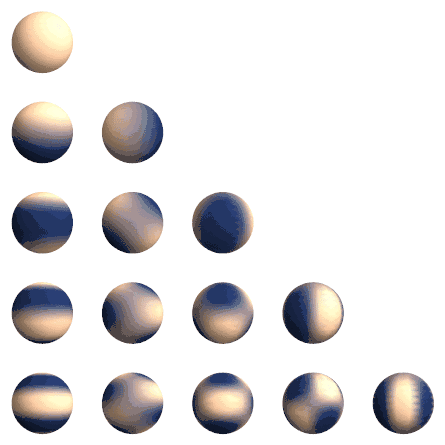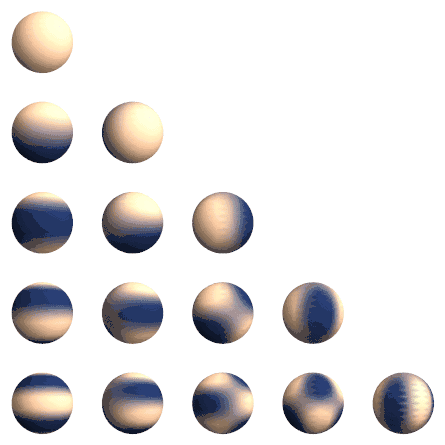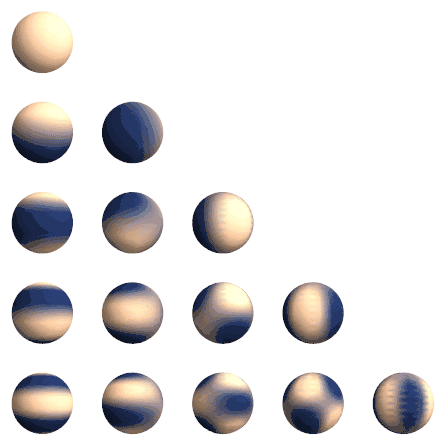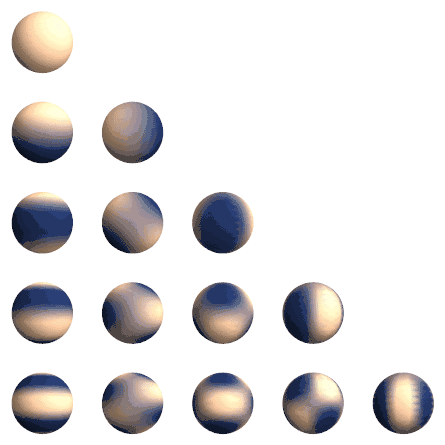
معادله لاپلاس در مختصات کروی به شکل زیر است:

${\displaystyle \nabla ^{2}f={1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r}\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right)+{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}=0}$

با تبدیل ‎f(r,θ،φ)=R(r)Θ(θ)Φ(φ)‎ ، بخش زاویه‌ای معادلهٔ لاپلاس در شرط زیر صدق می‌کند:

${\displaystyle {\Phi (\varphi ) \over \sin \theta }{d \over d\theta }\left(\sin \theta {d\Theta \over d\theta }\right)+{\Theta (\theta ) \over \sin ^{2}\theta }{d^{2}\Phi \over d\varphi ^{2}}+l(l+1)\Theta (\theta )\Phi (\varphi )=0.}$

با به‌کاربردن روش جداسازی متغیرها به دو معادله دیفرانسیل زیر می‌رسیم:

${\displaystyle {\frac {1}{\Phi (\varphi )}}{\frac {d^{2}\Phi (\varphi )}{d\varphi ^{2}}}=-m^{2}}$

${\displaystyle l(l+1)\sin ^{2}(\theta )+{\frac {\sin(\theta )}{\Theta (\theta )}}{\frac {d}{d\theta }}\left[\sin(\theta ){\frac {d\Theta }{d\theta }}\right]=m^{2}}$

برای هر m و l. بنابراین می‌توان نشان داد که بخش زاویه‌ای جواب، حاصل‌ضرب توابع مثلثاتی و توابع وابسته لژاندر هستند:

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )=N\,e^{im\varphi }\,P_{\ell }^{m}(\cos {\theta }),}$

که در آن ${\displaystyle Y_{\ell }^{m}}$ هماهنگ کروی درجهٔ ${\displaystyle \ell }$ و مرتبهٔ m خوانده می‌شود و ${\displaystyle P_{\ell }^{m}}$ تابع وابسته لژاندر است، N ثابت بهنجارش است و θ و φ به ترتیب زاویه با محور z (متمم عرض جغرافیایی) و زاویهٔ قطبی (طول جغرافیایی) هستند.

در ویکی‌انبار پرونده‌هایی دربارهٔ هماهنگ‌های کروی موجود است.

• هماهنگ‌های کروی در وب‌گاه MathWorld