طرح ترکیبیاتی

نظریه طرح ترکیبیاتی بخشی از ریاضیات ترکیبیاتی است که با وجود، ساخت و خواص دستگاه های مجموعه های متناهی سروکار دارد. آرایش این دستگاه ها مفاهیم تعمیم یافته ای از تعادل و/یا تقارن را ارضاء می کند. این مفاهیم هنوز معانی دقیق خود را پیدا نکرده اند، لذا اشیاء گسترده ای را می توان زیر یک چتر جمع کرد. بعضی مواقع چیزی که مهم است تعداد اعضای موجود در اشتراک مجموعه هاست، مثل طرح بلوک ها، و در مواقع دیگر آرایش فضایی اهمیت پیدا می کند، مثل شبکه های سودوکو.

نظریه طرح ترکیبیاتی را می توان به حوزه طرح آزمایشات اعمال کرد. برخی از نظریات پایه ای در مورد طرح های ترکیبیاتی در طرح آزمایشات زیستی آماردان و ژنتیک دان بریتانیایی به نام رونالد فیشر ظهور کرد. کاربرد های مدرنی نیز برای طرح آزمایشات در حوزه های گسترده ای وجود دارد چون: هندسه متناهی، برنامه ریزی تورنمنت، بخت آزمایی ها، شیمی ریاضیاتی، زیست ریاضیاتی، طراحی و تحلیل الگوریتم، شبکه سازی، آزمایش گروهی و رمزنگاری.[1]

مثال
صفحه فانو

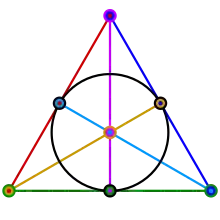
اگر نفر داشته باشیم، آیا این امکان وجود دارد که آن ها در مجموعه ها تقسیم گردند به گونه ای که هر نفر حداقل در یک مجموعه قرار گرفته و هر جفت از آن ها دقیقاً در یک مجموعه بوده، هر دو مجموعه دقیقاً در یک فرد مشترک بوده، و هیچ مجموعه ای شامل همه افراد، همه جز یک نفر، یا دقیقاً یک نفر نباشند؟ جواب بستگی به دارد.

این سوال تنها زمانی جواب دارد که به شکل باشد. اثبات این که اگر به شکل توانی از یک عدد اول باشد آنگاه سؤال فوق جوابی خواهد داشت، کمی سخت تر است. حدسی وجود دارد که می گوید این دو مدل جواب تنها جواب های سؤال فوق اند. همچنین نشان داده شده است که اگر جوابی برای همنهشت با 1 یا 2 به هنگ 4 وجود داشته باشد آنگاه به صورت جمع دو عدد مربع (توان دو) خواهد بود. نتیجه اخیر، یعنی قضیه بروک-ریسر، توسط ترکیب روش های ساختاری بر اساس میدان های متناهی و کاربردی از فرم های مربعی اثبات شده است.

وقتی چنین ساختاری وجود داشته باشد، آن را صفحه تصویری گویند؛ که به وسیله آن می توان نشان داد که چگونه هندسه متناهی و ترکیبیات با هم اشتراک پیدا می کنند. زمانی که باشد، صفحه تصویری را صفحه فانو گویند.

تاریخچه

طرح های ترکیبیاتی به زمان باستان بر می گردند، مربع لوشو مثالی از اولین مربع های جادوییست. یکی از اولین کاربرد های ثبت شده طرح های ترکیبیاتی در کتاب Brhat Samhita نوشته شده در حدود 587 قبل از میلاد توسط Varahamihira پیدا شده است. در این کتاب از یک مربع جادویی برای ساخت عطر با 4 ماده از بین 16 ماده استفاده شده است.[2]

طرح های ترکیبیاتی همراه با رشد عمومی ترکیبیات از قرن هجدهم توسعه یافت، مثل مربع های لاتین در قرن هجدهم و دستگاه های اشتاینر در قرن نوزدهم. همچنین طرح ها در سرگرمی های ریاضیاتی چون مسئله دخترمدرسه ای کرکمن (1850 میلادی)، و در مسائل عملی چون تورنمنت های نوبت گردشی (اثبات آن در دهه 1880 ارائه شده است)، محبوبیت داشته است. در قرن بیستم طرح ها در حوزه طرح آزمایشات به کار برده شدند، بخصوص مربع های جادویی، هندسه متناهی و اسکیم های انجمنی که به حوزه آمار جبری می انجامد.

یادداشت ها
  1. Stinson 2003, pg.1
  2. Hayashi, Takao (2008). "Magic Squares in Indian Mathematics". Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures (2 ed.). Springer. pp. 1252–1259. doi:10.1007/978-1-4020-4425-0_9778.

منابع
  • Assmus, E.F.; Key, J.D. (1992), Designs and Their Codes, Cambridge: Cambridge University Press, ISBN 0-521-41361-3
  • Beth, Thomas; Jungnickel, Dieter; Lenz, Hanfried (1986), Design Theory, Cambridge: Cambridge University Press. 2nd ed. (1999) شابک ‎۹۷۸−۰−۵۲۱−۴۴۴۳۲−۳ .
  • Bose, R. C. "A Note on Fisher's Inequality for Balanced Incomplete Block Designs". Annals of Mathematical Statistics. 1949: 619–620.
  • Caliński, Tadeusz; Kageyama, Sanpei (2003). Block designs: A Randomization approach, Volume II: Design. Lecture Notes in Statistics. 170. New York: Springer-Verlag. ISBN 0-387-95470-8.
  • Colbourn, Charles J.; Dinitz, Jeffrey H. (2007), Handbook of Combinatorial Designs (2nd ed.), Boca Raton: Chapman & Hall/ CRC, ISBN 1-58488-506-8
  • Fisher, R. A. (1940). "An examination of the different possible solutions of a problem in incomplete blocks". Annals of Eugenics. 10: 52–75. doi:10.1111/j.1469-1809.1940.tb02237.x.
  • Hall, Jr., Marshall (1986), Combinatorial Theory (2nd ed.), New York: Wiley-Interscience, ISBN 0-471-09138-3
  • Hughes, D.R.; Piper, E.C. (1985), Design theory, Cambridge: Cambridge University Press, ISBN 0-521-25754-9
  • Lander, E. S. (1983), Symmetric Designs: An Algebraic Approach, Cambridge: Cambridge University Press
  • Lindner, C.C.; Rodger, C.A. (1997), Design Theory, Boca Raton: CRC Press, ISBN 0-8493-3986-3
  • Raghavarao, Damaraju (1988). Constructions and Combinatorial Problems in Design of Experiments (corrected reprint of the 1971 Wiley ed.). New York: Dover.
  • Raghavarao, Damaraju and Padgett, L.V. (2005). Block Designs: Analysis, Combinatorics and Applications. World Scientific.
  • Ryser, Herbert John (1963), "Chapter 8: Combinatorial Designs", Combinatorial Mathematics (Carus Monograph #14), Mathematical Association of America
  • S. S. Shrikhande, and Vasanti N. Bhat-Nayak (1970) "Non-isomorphic solutions of some balanced incomplete block designs I", Journal of Combinatorial Theory
  • Stinson, Douglas R. (2003), Combinatorial Designs: Constructions and Analysis, New York: Springer, ISBN 0-387-95487-2
  • Street, Anne Penfold; Street, Deborah J. (1987). Combinatorics of Experimental Design. Oxford U. P. [Clarendon]. pp. 400+xiv. ISBN 0-19-853256-3.
  • van Lint, J.H., and R.M. Wilson (1992), A Course in Combinatorics. Cambridge, Eng.: Cambridge University Press.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.