روش پس‌گرد

پسگرد همه حالت‌های ممکن را برای جواب بررسی می‌کند تا حالت درست را بیابد. این یک جستجوی عمق اول بین جواب‌های ممکن است. هنگام جستجو اگر راهی که طی می‌شود نتیجه نداد (به جواب نرسید) به نقطهٔ قبلی بازمی گردد و راه بعدی را امتحان می‌کند. اگر همه راه‌ها را امتحان کرد و به جواب نرسید، جستجو نا موفق بوده‌است. این الگوریتم معمولاً در قالب توابع بازگشتی پیاده‌سازی می‌شود. به این صورت که در هر بار فراخوانی تابع، با اضافه شدن یک متغیر به‌طور متناوب همهٔ مقادیر ممکن را به آن نسبت می‌دهد و آن مقداری که با فراخوانی‌های بازگشتی بعدی سازگار است را ذخیره می‌کند. روش پسگرد را می‌توان یک پیاده‌سازی بازگشتی از جستجوی عمق-اول دانست. [1] [2]

یکی از استفاده‌های رایج از این الگوریتم، پیاده‌سازی عبارات باقاعده است. برای مثال الگوی سادهٔ "a*a" بدون استفاده از روش پسگرد با عبارت "aa" سازگار دیده نمی‌شود (چون a دوم با * از بین می‌رود و چیزی برای تطابق با a آخر وجود ندارد.) یکی دیگر از موارد استفاده از پسگرد، الگوریتم‌های مسیریاب است که با رفت و برگشت بر روی راس‌های یک گراف، کم هزینه‌ترین مسیر را پیدا می‌کند. همچنین استراتژی پسگرد در پیاده‌سازی زبان‌های برنامه نویسی و چیزهای دیگر مانند تجزیه متن‌ها کاربرد دارد.

الگوریتم پیمایش وارونه مجموعه‌ای از زیر مسئله‌ها را می‌شمارد که می‌توانند از طریق راه‌های مختلف کامل شوند و همهٔ راه حل‌های مسئله داده شده را بدهند. کامل شدن به صورت مرحله‌ای و قدم به قدم انجام می‌گیرد. زیر مسئله‌ها گره‌های یک درخت هستند. فرزندهای هر گره زیر مسئله‌هایی هستند که یک قدم کامل تر هستند. برگ‌ها زیر مسئله‌هایی هستند که دیگر نمی‌توانند افزایش یابند. الگوریتم پیمایش وارونه این درخت را به صورت بازگشتی با شروع از ریشه به صورت جستجوی اول عمق جستجو می‌کند. در هر گره c این الگوریتم امتحان می‌کند که آیا c می‌تواند به صورت یک جواب معتبر کامل شود. اگر نتواند زیر درخت به ریشه c قطع می‌شود. در غیر این صورت امتحان می‌کند که آیا c خودش یک جواب معتبر است. اگر بود آن را به کاربر بر می‌گرداند. سپس به صورت بازگشتی زیر درخت‌های c را پیمایش می‌کند.

برای بکار بردن پیمایش وارونه برای دستهٔ خاصی از مسئله‌ها.P را برابر یک نمونه از مسئله که باید حل بشود در نظر می‌گیریم. و ۶ تابع که p را به صورت یک پارامتر می‌گیرند، اولین فرزند c را بر می‌گرداند.

1. (next(P,s:برادر بعدی s را بر می‌گرداند.
2. (output(P,c:این تابع c را که جوابی برای P است چاپ می‌کند.

ابتدا ((bt(root(P را صدا می‌زنیم.

   if reject(P,c) then return
   if accept(P,c) then output(P,c)
   s ← first(P,c)
   while s ≠ Λ do
     bt(s)
     s ← next(P,s)

تابع reject باید boolean باشد و زمانی درست برگرداند که مطمئن باشد c به جواب نمی‌رسد. یک درست دادن اشتباه ممکن است باعث شود که bt به برخی از جواب‌ها نرسد. در عین حال کارایی پیمایش وارونه به درست برگرداندن reject برای زیر مسئله‌های نزدیک ریشه بستگی دارد. اگر همواره غلط برگرداند الگوریتم تبدیل به جست‌جوی کامل می‌شود. توابع first و next فرزندان زیر مسئله c را پیمایش می‌کند. اگر فرزند مورد نظر نبود این دو تابع باید null برگردانند.

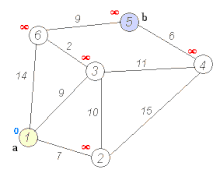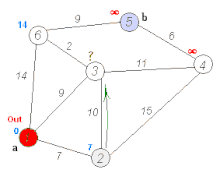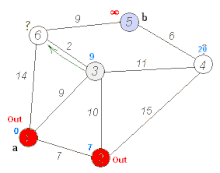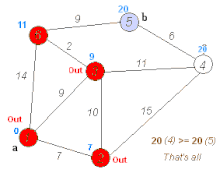
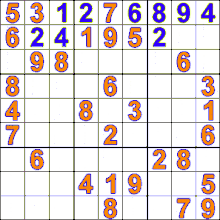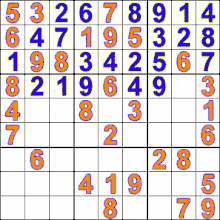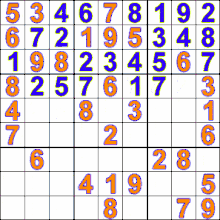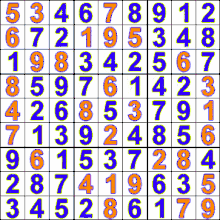
• مثال‌هایی از اجرای این الگوریتم (میز , الگوریتم دایسترا , شطرج , سودوکو , مارپیچ)
• 
• 
• 
• 
• 

• ویکی‌پدیای انگلیسی

• قفل رمزی
• روش تقسیم و حل
• جستجوی عمق اول