تخصیص پنهان دیریکله
تخصیص پنهان دیریکله (به انگلیسی: Latent Dirichlet Allocation) یا LDA یک مدل تولیدی در آمار است. این مدل برای مدل سازی تعدادی متغیرهای پنهان (عناوین) در مجموعهای از متنها که شامل کلمات هستند به وجود آمدهاست. در حقیقت در یک متن شامل تعدادی کلمه میتوان به هر کلمه تعدادی عنوان با احتمال مشخص نسبت داد که در نهایت با ترکیب با هم یک متن و عنوان آن را تشکیل میدهند.[1]
عناوین در LDA
در واقع میتوان هر متن را به عنوان یک توزیع مخلوط از عناوین دید. این مشابه آنالیز پنهان مفهومی احتمالی با این تفاوت که در LDA یک توزیع احتمال پیشین از نوع توزیع دریکله در نظر گرفته میشود. اگرچه LDA با توزیع دریکله یکنواخت معادل با آنالیز پنهان مفهومی احتمالی است.[2]
هر عنوان مجموعه ای از کلمات را با احتمال مشخصی ایجاد میکند. کلماتی که تعلق خاصی به برخی از عناوین ندارند (مانند the در انگلیسی) میتوان آنها را با احتمال یکنواختی در هرکدام از عناوین قرار داد؛ یا اینکه آنها را دستهٔ خاصی قرار داد. باید توجه کرد که تعریف صریحی برای عنوان از دیدگاههای معناشناسی یا معرفتشناسی مشخص نمیشود. بلکه اختصاص عناوین با یادگیری با نظارت برخی از کلمات و اختصاص آنها به عناوین و میزان رخدادهای آنها انجام میشود.
نکتهٔ دیگر این است که در این مدل چیزی برای مدلسازی ترتیب یا همبستگی عناوین در نظر گرفته نمیشود، و هر متن به عنوان کیسه کلمات در نظرگرفته شده و فرض تعویض پذیری (تئوری دی فینتی) انجام میشود.
مدل

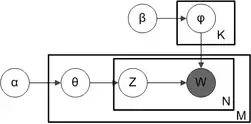
در شکل مدل LDA نمایش داده شدهاست. M تعداد متنها و N تعداد کلمات در هر متن است. پارامترهای مدل عبارتند از:
- α پارامتر توزیع پیشین دیریکله برای عناوین به ازای هر متن است.
- β پارامتر توزیع پیشین دیریکله برای توزیع کلمات به ازای هر عنوان است.
- توزیع عناوین برای متن i-ام است.
- توزیع کلمات برای عنوان k-ام است.
- متغیر پنهان عنوان j-امین کلمه در i-امین متن است.
- j-امین کلمه در i-امین متن است.
- V تعداد واژه هاست.
- ماتریس K*V توزیع کلمات به ازای هر عنوان است.
تنها متغیرهای مشاهده شده بقیه متغیر پنهان پنهان هستند.
اکنون میتوان کل دادهها را ایجاد شده از طریق مدل فرض شده بر اساس متغیرهای پنهان در نظر گرفت:
۱. انتخاب توزیع دیریکله به ازای .
۲. انتخاب توزیع به ازای .
۳. به ازای هر کلمه
- ۱٫۱ انتخاب عنوان
- ۱٫۲ انتخاب کلمهٔ
تعریف ریاضی
جستارهای وابسته
منابع
- Blei, David M.; Ng, Andrew Y.; Jordan, Michael I (2003). Lafferty, John, ed. "Latent Dirichlet allocation". Journal of Machine Learning Research. 3 (4–5): pp. 993&ndash, 1022. doi:10.1162/jmlr.2003.3.4-5.993. Archived from the original on 1 May 2012. Retrieved 5 February 2013. Unknown parameter
|month=ignored (help) - Girolami, Mark (2003). On an Equivalence between PLSI and LDA (PDF). Proceedings of SIGIR 2003. New York: Association for Computing Machinery. شابک ۱−۵۸۱۱۳−۶۴۶−۳. Unknown parameter
|coauthors=ignored (|author=suggested) (help)
