برنامهسازی غیرخطی
در ریاضیات، برنامهسازی غیر خطی Nonlinear programming (NLP) فرایند حل مسئله بهینه سازی است که در آن برخی از محدودیت ها یا خود تابع هدف غیر خطی است. این مسئله بهینه سازی، یک سیستم از برابریها و نابرابریها بر روی مجموعهای از متغیرهای ناشناخته حقیقی، در یک تابع هدف که باید کمینه یا بیشینه شود.
روشهای برنامه سازی غیر خطی
روش لاگرانژ
در این روش تابع هدف به صورت تابع F در نظر گرفته میشود.
این تابع بر زیرمجموعهای چون X از فضای اقلیدسی تعریف شدهاست (پس عناصر X میتوانند بردار باشند). این زیرمجموعه، توسط قیود به شکل g(x)=b تعریف میشود. تابع لاگرانژ در این حالت عبارت خواهد بود از: ((L(x،y)=F(x)+y.(b-g(x
شرایط لازم برای حل مسئله را میتوان از طریق یافتن نقاط بحرانی تابع لاگرانژ (ماکزیممسازی بدون قید) به دست آورد.
روش برنامهریزی مرتبه دوم
برنامهریزی مرتبه دوم(QP) روشی برای مینیمم سازی توابع مرتبه دوم n متغیره با m محدودیت خطی نامساوی یا مساوی یا هر دو است.
مسائل برنامهریزی مرتبه دوم سادهترین فرم مسائل برنامهریزی غیر خطی با محدودیت نا مساوی میباشد.
روش گرادیان کاهش یافته عمومی
این الگوریتم برای محدودیتهای خطی اصلاح شده که تابع هدف و محدودیت آنها غیر خطی است محسوب میشود. در اصل روش محدودیتهای خطی یا خطی شده را شامل میشود و متغیر جدید با محدودیت تعریف خواهد شد. بیشتر روشهای حل مسائل برنامهریزی غیر خطی عمومی شامل خطی کردن مسئله و به کار بردن تکنیک برنامهریزی خطی است که بهطور خلاصه مراحل زیر طی میشود.
- به دست آوردن مدل با نقاط عملیاتی و خطی کردن تمام محدودیتهای تابع هدف حول نقاط عملیاتی. بطوریکه مسئله به فرم برنامهریزی خطی تبدیل شود. سپس استفاده از برنامهریزی خطی برای حل مسئله خطی.
- تکرار روش برنامهریزی خطی برای رسیدن به جواب مناسب با خطی کردن توابع محدودیتها و تابع هدف و چنانچه به جواب مناسب نرسید با خطی کردن دوباره محدودیتها و توابع هدف حول نقطه جدید optimum مسئله پیدا میشود.
در روشهای ذکر شده ممکن است روش به همگرایی نرسد و این خود یکی از معایب روشهای فوق است به واقع بهترین الگوریتم عمومی حاضر استفاده از الگوریتم گرادیان کاهش یافته عمومی است.
کاربرد برنامه سازی غیر خطی
یکی از مسائل پرکاربرد و معمول برای توابع غیر خطی و برنامهسازی غیر خطی مسائل مربوط به بهینهسازی است. مثلاً بهینهسازی هزینه حمل و نقل با انتخاب روش یا روشهایی از میان چندین روش نقل و انتقال است که هرکدام ظرفیتها و محدودیتهای متفاوتی دارند. به عنوان مثال نقل و انتقال نفت خام با انتخاب روشهای ترکیبی از خط لوله، تانکر، راه آهن، حمل کنندههای دریایی که هرکدام توابع هزینهای متفاوتی دارند میتواند در نهایت به ما یک تابع غیر خطی از هزینه بدهد.
نمایش فرمولی مسئلههای بهینهسازی
مسئله بهینهسازی میتواند به صورتهای مختلفی بیان شود مثلاً یکی از سادهترین حالتها این است که به صورت زیر بیان شود:
برای بیشینه کردن بعضی از متغیرها مانند توان عملیاتی محصول یا
برای کمینه کردن تابع هزینه در جایی که داریم:
روشهای حل مسئله
اگر تابع هدف مسئله به صورت f یک تابع خطی باشد و فضای محدوده یک Polytope باشد این مسئله یک مسئله برنامهنویسی خطی است که با روشهای خطی شناخته شده به راحتی حل میشود.
اگر تابع هدف یک تابع Concave (مسئله به حداکثر رسانی) یا یک تابع Convex (مسئله به حداقل رسانی) باشد و محدودیتها از نوع محدب (convex) باشد، آنگاه مسئله یک مسئله محدب (convex) نامیده میشود و روشها و متدهای عمومی برای بینه سازی محدب (Convex Optimization)میتوانند در اغلب این مسئلهها مورد استفاده قرار گیرند. اگر تابع هدف نسبت تابعی مقعر (Concave) و محدب (Convex) باشد و محدودیتها به صورت محدب باشد، این مسئله میتواند به یک مسئله بهینهسازی محدب تبدیل شود که در آن از تکنیکهای برنامهنویسی کسری استفاده میشود.
روشها و متدهای زیادی برای حل مسئلههای غیر محدب وجود دارند. یکی از این روشها استفاده از فرمولاسیونهای ویژه مسائل برنامهنویسی خطی است. یکی دیگر از این روشها استفاده از روش شاخه و حد است که مسئله در آن به زیر بخشهایی برای حل به صورت محدب یا تقریب خطی تقسیم میشود.
مثالها
نمونه دو بعدی
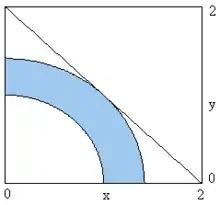
یک مسئله ساده میتواند با محدودیتهای زیر تعریف شود:
- x۱ ≥ ۰
- x۲ ≥ ۰
- x۱۲ + x۲۲ ≥ ۱
- x۱۲ + x۲۲ ≤ ۲
با تابع هدفی به صورت زیر که باید بیشینه شود:
- f(x) = x۱ + x۲
درحالی که: (x = (x۱، x۲.
نمونه سه بعدی
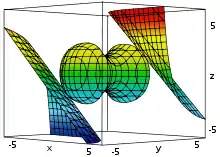
نمونه دیگری از مسئله میتواند به صورت زیر تعریف شود:
- x۱۲ − x۲۲ + x۳۲ ≤ ۲
- x۱۲ + x۲۲ + x۳۲ ≤ ۱۰
با تابع هدفی به صورت زیر که باید بیشینه شود:
- f(x) = x۱x۲ + x۲x۳
درحالی که: (x = (x۱، x۲، x۳.
منابع
Bertsekas, Dimitri P. (1999). Nonlinear Programming (Second ed.). Cambridge, MA.: Athena Scientific. ISBN 1-886529-00-0.
منابع برای مطالعه بیشتر
- Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.
- Bazaraa, Mokhtar S. and Shetty, C. M. (1979). Nonlinear programming. Theory and algorithms. John Wiley & Sons. ISBN 0-471-78610-1.
- Bertsekas, Dimitri P. (1999). Nonlinear Programming: 2nd Edition. Athena Scientific. ISBN 1-886529-00-0.
- Bonnans, J. Frédéric; Gilbert, J. Charles; Lemaréchal, Claude; Sagastizábal, Claudia A. (2006). Numerical optimization: Theoretical and practical aspects. Universitext (Second revised ed. of translation of 1997 French ed.). Berlin: Springer-Verlag. pp. xiv+490. doi:10.1007/978-3-540-35447-5. ISBN 3-540-35445-X. MR 2265882.
- Luenberger, David G.; Ye, Yinyu (2008). Linear and nonlinear programming. International Series in Operations Research & Management Science. 116 (Third ed.). New York: Springer. pp. xiv+546. ISBN 978-0-387-74502-2. MR 2423726.
- Nocedal, Jorge and Wright, Stephen J. (1999). Numerical Optimization. Springer. ISBN 0-387-98793-2.
- Jan Brinkhuis and Vladimir Tikhomirov, 'Optimization: Insights and Applications', 2005, Princeton University Press
