بازی ازدحامی

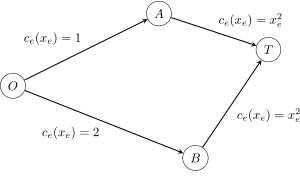
یک شبکهٔ ترافیکی را در نظر بگیرید که دو بازیکن از نقطهٔ O حرکت خود را آغاز می‌کنند و می‌خواهند به نقطهٔ T برسند. فرض کنید نقطهٔ O با مسیرهای ارتباطی A و B به نقطهٔ T متصل است، به صورتی که مسیر A کمی از مسیر B طول کمتری دارد (به عبارت دیگر مسیر A با احتمال بیشتری توسط هر بازیکن انتخاب می‌شود). اما هردو راه ارتباطی به سادگی شلوغ می‌شود؛ به این معنا که هر چه تعداد بازیکن بیشتری از یک مسیر عبور کنند تأخیر هر بازیکن بیشتر می‌شود. در نتیجه عبور هر دو بازیکن از مسیر یکسان باعث تأخیر اضافی خواهد شد. نتیجهٔ مطلوب در این بازی درصورتی کسب می‌شود که دو بازیکن همکاری کرده و از مسیرهای متفاوتی عبور کنند. آیا می‌توان چنین نتیجه‌ای گرفت؟ و اگر چنین است، هزینهٔ هر بازیکن چه خواهد بود؟

بازی‌های ازدحامی گسسته دارای اجزای زیرند:

• یک مجموعه از عناصر ازدحام‌پذیر ${\displaystyle E}$
• ${\displaystyle n}$ بازیکن
• یک مجموعه متناهی از استراتژی‌های ${\displaystyle S_{i}}$ برای هر بازیکن بدین صورت که هر استراتژی ${\displaystyle P\in S_{i}}$ زیرمجموعه‌ای از ${\displaystyle E}$ می‌باشد.
• به‌ازای هر عنصر ${\displaystyle e}$ و یک بردار از استراتژی‌های ${\displaystyle (P_{1},P_{2},\ldots ,P_{n})}$ ، باری که این عنصر متحمل می‌شود به صورت ${\displaystyle x_{e}=\#\{i:e\in P_{i}\}}$ می‌باشد.
• به‌ازای هر عنصر ${\displaystyle e}$، یک تابع تأخیر به صورت ${\displaystyle d_{e}:\mathbb {N} \longrightarrow \mathbb {R} }$
• به‌ازای استراتژی ${\displaystyle P_{i}}$ داده شده، بازیکن ${\displaystyle i}$ تأخیری معادل ${\displaystyle \textstyle \sum _{e\in P_{i}}d_{e}(x_{e})}$ متحمل می‌شود. فرض کنید که هر ${\displaystyle d_{e}}$ مثبت و صعودی به صورت یکنواخت است.

گراف جهت‌دار زیر را در نظر بگیرید. هر بازیکن دو استراتژی برای انتخاب دارد تا از A به B برسد. در نتیجه در کل ۴ حالت برای رسیدن بازیکنان به مقصد موجود است. ماتریس زیر، هزینهٔ بازیکنان را به صورت تأخیری که بسته به انتخابشان متحمل می‌شوند، نشان می‌دهد.

گراف جهت‌دار یک بازی ازدحامی ساده

در این بازی، استراتژی‌های (A,B) و (B,A) تعادل نش خالص هستند. این بدین دلیل است که هر تغییری توسط هر بازیکن باعث افزایش هزینهٔ او می‌شود (توجه کنید که اعداد جدول هزینه را نشان می‌دهند. در نتیجه بازیکنان مقادیر کوچکتر را ترجیح می‌دهند)

وجود تعادل نش را می‌توان با ساختن یک تابع پتانسیلی که به هر وضعیت خروجی یک مقدار نسبت می‌دهد اثبات کرد. علاوه بر این، ساختن این تابع نشان می‌دهد یافتن بهترین پاسخ به صورت تکرارشونده به تعادل نش منجر می‌شود. تابع ذکرشده را به صورت ${\displaystyle \textstyle \Phi =\sum _{e\in E}\sum _{k=1}^{x{e}}d_{e}(k)}$ تعریف می‌کنیم. توجه کنید که این تابع همان رفاه اجتماعی ${\displaystyle \textstyle \sum _{e\in E}x_{e}d_{e}(x_{e})}$ نیست؛ بلکه بیشتر یک نوع انتگرال گسسته محسوب می‌شود. ویژگی اصلی تابع پتانسیلی این است که اگر یک بازیکن استراتژی خود را تفییر دهد، تغییر تأخیر او برابر با تغییر در تابع پتانسیل باشد.
حالتی را در نظر بگیرید که بازیکن ${\displaystyle i}$ استراتژی خود را از ${\displaystyle P_{i}}$ به ${\displaystyle Q_{i}}$ تغییر می‌دهد. عناصری که در هر دو استراتژی هستند بدون تغییر باقی می‌مانند و عناصری که این بازیکن آن‌ها را رها می‌کند (به عبارت دیگر ${\displaystyle e\in P_{i}-Q_{i}}$) تابع پتانسیل را به مقدار ${\displaystyle d_{e}(x_{e})}$ کاهش می‌دهند و همچنین عناصری که این بازیکن به آن‌ها می‌پیوندد (به عبارت دیگر ${\displaystyle e\in Q_{i}-P_{i}}$) تابع پتانسیلی را به اندازهٔ ${\displaystyle d_{e}(x_{e}+1)}$ افزایش می‌دهند. این تغییر در پتانسیل دقیقاً با تغییر تأخیر برای این بازیکن برابر می‌باشد. در نتیجه تابع تعریف‌شده در حقیقت یک تابع پتانسیل می‌باشد.

بازی‌های ازدحامی پیوسته حالت حدی این نوع بازی‌ها به‌طوری‌که ${\displaystyle n\rightarrow \infty }$ هستند. در این حالت، بازیکنان را بی‌نهایت کوچک در نظر می‌گیریم. همچنان ${\displaystyle E}$ را مجموعهٔ متناهی از عناصر ازدحام‌پذیر تعریف می‌کنیم. درعوض به‌جای مشخص کردن ${\displaystyle n}$بازیکن در حالت گسسته، ${\displaystyle n}$ نوع بازیکن داریم به صورتی که هر نوع بازیکن ${\displaystyle i}$به ${\displaystyle r_{i}}$ که نشان‌دهندهٔ نرخ ترافیک برای آن نوع است، مرتبط است. هر نوع بازیکن یک استراتژی از مجموعه ${\displaystyle S_{i}}$ که مجزا در نظر گرفته می‌شوند،را انتخاب می‌کند. همانند قبل، فرض کنید که ${\displaystyle d_{e}}$ یکنوا و مثبت می‌باشد اما فرض پیوسته بودن را هم به آن‌ها اضافه می‌کنیم. درنهایت، به بازیکنان از یک نوع اجازه می‌دهیم به‌طور نسبی بین مجموعهٔ استراتژی‌شان توزیع شوند. بدین صورت که به ازای استراتژی ${\displaystyle P\in S_{i}}$ مقدار ${\displaystyle f_{P}}$ برابر با کسری از بازیکنان نوع ${\displaystyle i}$ که از استراتژی ${\displaystyle P}$ استفاده می‌کنند، می‌باشد. فرض کنید داریم: ${\displaystyle \textstyle \sum _{P\in S_{i}}f_{P}=r_{i}}$.

توجه کنید در این حالت استراتژی‌ها مجموعه استراتژی پروفایل‌های ${\displaystyle f_{P}}$ می‌باشند. برای یک مجموعه استراتژی ${\displaystyle S_{i}}$ با اندازهٔ ${\displaystyle n}$ ، مجموعهٔ تمام پروفایل‌های معتبر زیرمجموعهٔ فشرده‌ای از ${\displaystyle [0,r_{i}]^{n}}$ می‌باشد. همانند قبل، تابع پتانسیل را به صورت ${\displaystyle \textstyle \Phi =\sum _{e\in E}\int _{0}^{x{e}}d_{e}(z)\,dz}$ با جایگزینی انتگرال گسسته با نوع استاندارد آن، تعریف می‌کنیم.

به عنوان تابع استراتژی، ${\displaystyle \Phi }$به دلیل پیوسته بودن ${\displaystyle d_{e}}$و ${\displaystyle x_{e}}$، نیز پیوسته است. در نتیجه با توجه به قضیهٔ ارزش فوق‌العاده، ${\displaystyle \Phi }$مقدار کمینهٔ سراسری خود را می‌گیرد.

آخرین گام این است که نشان دهیم، کوچکترین مقدار ${\displaystyle \Phi }$ همان تعادل نش می‌باشد. فرض کنید برخلاف این، یک مجموعه ${\displaystyle f_{P}}$ موجود است به صورتی که مقدار ${\displaystyle \Phi }$را کمینه می‌کند اما تعادل نش نیست. سپس برای یک نوع ${\displaystyle i}$می‌توان ${\displaystyle Q}$ برای انتخاب کنونی ${\displaystyle P}$ بهبود داد. به عبارت دیگر داریم: ${\displaystyle \textstyle \sum _{e\in P}d_{e}(x_{e})>\sum _{e\in Q}d_{e}(x_{e})}$. حال مقدار کوجک ${\displaystyle \delta <f_{P}}$ را از بازیکنانی که استراتژی ${\displaystyle P}$ را دارند، می‌گیریم و آن‌ها را به استراتژی ${\displaystyle Q}$ تغییر می‌دهیم. حال، برای هر ${\displaystyle x_{e}\in Q}$، بار آن را با اندازهٔ ${\displaystyle \delta }$افزایش داده‌ایم. در نتیجه مقدار آن در ${\displaystyle \Phi }$، در این حالت برابر ${\displaystyle \textstyle \int _{0}^{x{e}+\delta }d_{e}(z)dz}$ می‌باشد. با مشتق گرفتن از از این انتگرال، تغییرات تقریباً برابر با ${\displaystyle \delta \cdot d_{e}(x_{e})}$ با خطای ${\displaystyle \delta ^{2}}$ خواهد بود. همین تحلیل تغییرات برای زمانی که به یال‌های داخل ${\displaystyle P}$ نگاه کنیم صادق خواهد بود.

بنابراین، تغییرات در پتانسیل تقریباً برابر با ${\displaystyle \textstyle \delta (\sum _{e\in Q}d_{e}(x_{e})-\sum _{e\in P}d_{e}(x_{e}))}$ که مقداری منفی است، می‌باشد. این تناقض بوده و نتیجه می‌گیریم ${\displaystyle \Phi }$ کمینه نشده‌است. در نتیجه، کمینهٔ ${\displaystyle \Phi }$ باید یک تعادل نش باشد.

به دلیل وجود تعادل نش در بازی‌های ادغامی پیوسته، طبعاً موضوع بعدی تجزیه و تحلیل کیفیت این تعادل‌ها می‌باشد. میزان کیفیت تعادل‌ها را به صورت نسبت مجموع تأخیر در تعادل نش و حالت بهینه که به هزینهٔ هرج و مرج معروف است، استخراج می‌کنیم. در ابتدا، با یک شرط بر روی توابع تأخیر کار را آغاز می‌کنیم:

تعریف تأخیر ${\displaystyle (\lambda ,\mu )}$ملایم است در صورتی که به ازای هر ${\displaystyle x,y>0}$ داریم: ${\displaystyle yd(x)\leq \lambda yd(y)+\mu xd(x)}$

حال اگر تأخیر ${\displaystyle (\lambda ,\mu )}$ملایم بود، ${\displaystyle f}$یک تعادل نش می‌باشد و ${\displaystyle f^{*}}$یک اختصاص بهینه منابع است و سپس داریم: ${\displaystyle \textstyle \sum _{e}x_{e}d_{e}(x_{e})\leq {\frac {\lambda }{1-\mu }}\sum _{e}x_{e}^{*}d_{e}(x_{e}^{*})}$. به عبارت دیگر، هزینهٔ هرج و مرج برابر با ${\displaystyle \textstyle {\frac {\lambda }{1-\mu }}}$می‌باشد. برای اثبات این مطلب می‌توانید به این نوشته مراجعه کنید.

بازی پتانسیل

• یادداشت‌های سخنرانی از یشای منصور در مورد پتانسیل و تراکم بازی‌ها
• ּبازی‌های تخصیص منابع[1] تا حدودی مربوط به بازی‌های ازدحامی می‌باشند.